Малый ромбододекаэдр своими руками
Добавил пользователь Skiper Обновлено: 08.09.2024
Презентация на тему: " Многогранники Ромбододекаэдр Новиков Денис 10А. Ромбододекаэдр Грань -Ромб Граней-12 Рёбер-24 Вершин-14 Граней при вершине- 4 грани при 6 вершинах 3 грани." — Транскрипт:
1 Многогранники Ромбододекаэдр Новиков Денис 10А
2 Ромбододекаэдр Грань -Ромб Граней-12 Рёбер-24 Вершин-14 Граней при вершине- 4 грани при 6 вершинах 3 грани при 8 вершинах Длина ребра-4 см Двойственный многогранник- Кубооктаэдр
3 Ромбододекаэдр S грани=14,625см 2 S поверхности=175,5см 2 Расстояние между || вершинами=9см Расстояние между || гранями=6,5см r=3,25см R-4,5см S вс=42,25p см 2 S ос=81p cм 2 V вс=45,8см 3 V ос=121,5см 3
4 Изгибаемые многогранники Первые примеры изгибаемых многогранников были построены бельгийским инженером и математиком Раулем Брикаром в 1897 году. Сейчас их называют октаэдрами Брикара. Они не только невыпуклые, но и имеют самопересечения, что не позволяет построить их движущуюся картонную модель.. Многогра?нник (точнее многогранная поверхность) называется изгиба?емым, если его пространственную форму можно изменить такой непрерывной во времени деформацией, при которой каждая грань не изменяет своих размеров (то есть движется как твёрдое тело), а деформация осуществляется только за счёт непрерывного изменения двугранных углов. Такая деформация называется непрерывным изгибанием многогранника.
Эта фигура на протяжении сотен лет привлекает к себе внимание зодчих и математиков — и не только своими необычными свойствами, но и эстетически безупречной формой.

Звездчатый ромбододекаэдр. Характерная для него схема заполнения пространства уникальна по своей красоте и изысканности.
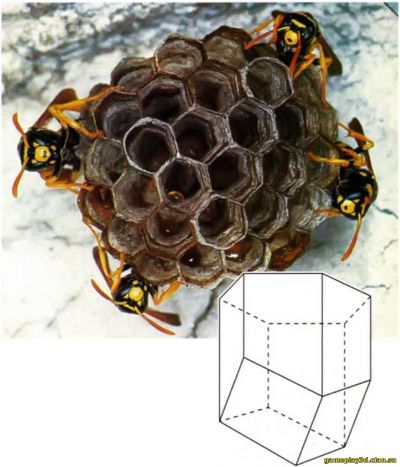
Почему пчелы предпочитают иметь дело именно с такими конструкциями? На протяжении всего XVIII в. ученые пытались ответить на этот вопрос.
Одно из тогдашних объяснений основывалось на том факте, что из всех фигур, полностью заполняющих пространство, подобные фигуры (при равном объеме) имеют наименьшую площадь. Получалось, что умные пчелы таким образом экономят воск, идущий на строительство сот.
Однако позднее выяснилось, что это утверждение было ошибочным. Нашлись другие способы завершения шестиугольной призмы, позволяющие сэкономить больше объема. Один из таких способов предоставляет усеченный восьмигранник. Другой вопрос — самый ли он экономичный? Многие исследователи до сих пор пытаются найти конечное решение этой проблемы, но пока безуспешно.

Что такое многогранник?
Многогранник называется правильным, если: а) он является выпуклым; б) все его грани образованы правильными многоугольниками; в) в каждой вершине сходится одинаковое число граней; г) все его двухгранные углы равны.
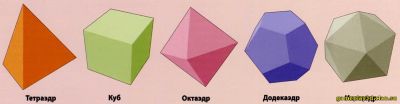
Доказано, что существует всего пять правильных многогранников (по-другому их еще называют Платоновыми телами): это тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.
Свойства многогранника Эшера
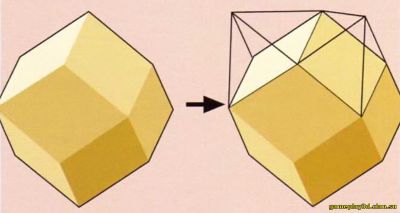
Как получать из обычных многоугольников и многогранников звездчатые многоугольники и многогранники?
Первый такой многоугольник образуется при модернизации правильного пятиугольника. Это пятиконечная звезда (так называемая пентаграмма) — в нашем отечестве слишком хорошо всем знакомая. Впрочем, у пентаграммы очень долгая история, она служила магическим символом еще пифагорейцам.

Продолжая стороны правильного пятиугольника, мы получим пятиконечную звезду — так называемую пентаграмму.
Правильные звездчатые многогранники
Существует лишь четыре правильных звездчатых многогранника — математики их называют телами Кеплера-Пу-ансо. Два из них открыл Иоганн Кеплер (1571—1630 гг.) в начале XVII в., другие два — Луи Пуансо (1777—1859 гг.) в 1809 г. Их названия: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Первые три образованы на основе додекаэдра, а последний — на основе икосаэдра.
Чтобы получить малый звездчатый додекаэдр, нужно продолжить 12 граней правильного додекаэдра. Другие звездчатые многогранники получаются посредством несколько более сложных операций. Грани малого и большого звездчатого додекаэдра представляют собой пентаграммы, а грани звездчатого икосаэдра образованы 20 равносторонними треугольниками.

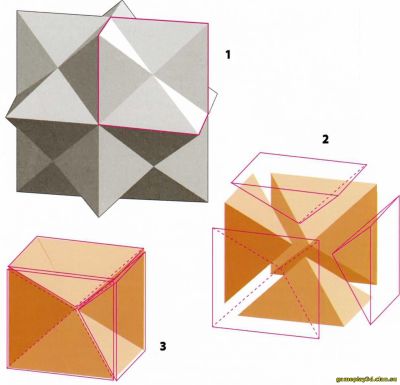
Решение головоломки
Для начала убедитесь, что все представленные справа детали головоломки одинаковы. При попытке собрать звездчатый ром бододекаэдр оказывается несложным соединить первые пять деталей; проблема возникает с добавлением к конструкции последней детали.

Наилучший способ решения головоломки заключается в построении сначала двух фигур, каждая из которых состоит из трех деталей головоломки. Их собирают таким образом, чтобы средние точки полученных фрагментов можно было совместить.
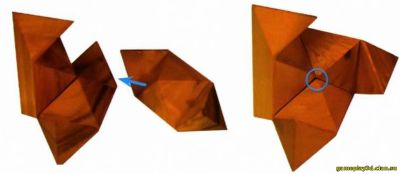
Обратите внимание, что ориентация полученных фигур разная.

На конец, берутся обе фигуры — по одной в каждую руку — и осторожно соединяются между собой. Теперь в руках у вас — звездчатый ромбододекаэдр собственной персоной.

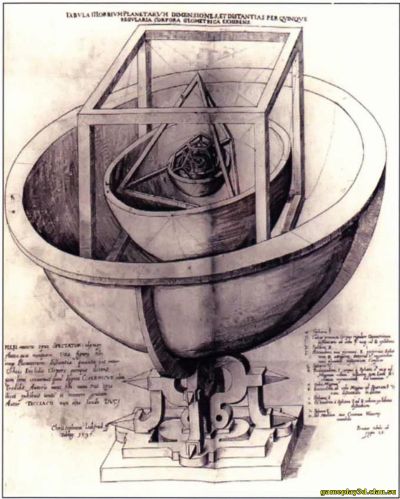
Иоганн Кеплер придумал эту модель вписанных правильных многогранников, чтобы наглядно показать соотношение расстояний между планетами Солнечной системы. Внешняя сфера, описывающая куб, соответствует орбите Сатурна, а внутренняя, описывающая тетраэдр, — орбите Юпитера.
Звёздчатый многогранник — это правильный невыпуклый многогранник. Многогранники из-за их необычных свойств симметрии исследуются с древнейших времён. Также формы многогранников широко используются в декоративном искусстве.
Звёздчатый октаэдр
Существует только одна звёздчатая форма октаэдра. Звёздчатый октаэдр был открыт Леонардо да Винчи, затем спустя почти 100 лет переоткрыт Иоганном Кеплером, и назван им Stella octangula — звезда восьмиугольная. Отсюда эта форма имеет и второе название stella octangula Кеплера. По сути она является соединением двух тетраэдров.

Звёздчатые формы додекаэдра
Додекаэдр имеет 3 звёздчатые формы: малый звездчатый додекаэдр, большой додекаэдр, большой звёздчатый додекаэдр(звёздчатый большой додекаэдр, завершающая форма). Первые две из них были открыты Кеплером (1619), третья — Пуансо (1809). В отличие от октаэдра любая из звёздчатых форм додекаэдра не является соединением платоновых тел, а образует новый многогранник.
Все 3 звёздчатые формы додекаэдра, вместе с большим икосаэдром образуют семейство тел Кеплера-Пуансо, то есть правильных невыпуклых (звёздчатых) многогранников.
У большого додекаэдра гранями являются пятиугольники, которые, сходятся по пять в каждой из вершин. У малого звёздчатого и большого звёздчатого додекаэдров грани - пятиконечные звёзды (пентаграммы), которые в первом случае сходятся по 5, а во втором по 3.
Вершины большого звёздчатого додекаэдра совпадают с вершинами описанного додекаэдра. У каждой вершины соединяются три грани.
Звёздчатые формы икосаэдра
Икосаэдр имеет 59 звёздчатых форм, из которых 32 обладают полной, а 27 неполной икосаэдральной симметрией, что было доказано Кокстером совместно с Дювалем, Флэзером и Петри c применением правил ограничения, установленных Дж. Миллером. Одна из этих звёздчатых форм (20-я, мод. 41 по Веннинджеру), называемая большим икосаэдром, является одним из четырёх правильных звёздчатых многогранников Кеплера—Пуансо. Его гранями являются правильные треугольники, которые сходятся в каждой вершине по пять; это свойство является у большого икосаэдра общим с икосаэдром.
Среди звёздчатых форм также имеются: соединение пяти октаэдров, соединение пяти тетраэдров, соединение десяти тетраэдров.
Икосаэдр имеет двадцать граней. Если каждую из них продолжить неограниченно, то тело будет окружено большим многообразием отсеков — частей пространства, ограниченных плоскостями граней. Все звёздчатые формы икосаэдра можно получить добавлением к исходному телу таких отсеков. Не считая самого икосаэдра, продолжения его граней отделяют от пространства 20+30+60+20+60+120+ 12+30+60+60 отсеков десяти различных форм и размеров. Большой икосаэдр (см. рис) состоит из всех этих кусков, за исключением последних шестидесяти.
Звёздчатые формы кубооктаэдра
Кубооктаэдр имеет 4 звёздчатые формы, удовлетворяющие ограничениям, введённым Миллером. Первая из них является соединением куба и октаэдра.
Звёздчатые формы икосододекаэдра
Икосододекаэдр имеет множество звёздчатых форм.
Икосододекаэдр имеет 32 грани, из которых 12 являются правильными пятиугольными гранями, а остальные 20 — правильные треугольники. Что касается вопроса о том, могут ли получившиеся многогранники оказаться правильными, то на него давно получен ответ. Великий математик Коши ещё в 1811 году доказал, что список правильных многогранников исчерпывается пятью платоновыми телами вкупе с четырьмя многогранниками Кеплера — Пуансо.
Этот многогранник получается при продолжении граней додекаэдра. Его можно также получить из икосаэдра, вырезанием из его граней правильных треугольных пирамид.

Получается продолжением граней икосаэдра. Его можно также получить из малого звездчатого додекаэдра вырезанием из его граней треугольных пирамид.

Помимо правильных звездчатых многогранников (тел Кеплера-Пуансо) имеется более сотни различных звездчатых форм многогранников. На рисунке показаны звездчатые формы кубооктаэдра.

На рисунке показаны некоторые звездчатые формы икосаэдра. Всего их 59.

На рисунке показаны некоторые звездчатые формы икосододекаэдра. Всего их 19.

А вот ещё группа красавцев…
На рисунке изображен многогранник, называемый звездчатым октаэдром, получающийся продолжением граней октаэдра. Он был открыт Леонардо да Винчи, затем спустя почти сто лет переоткрыт И. Кеплером и назван им "Stella octangula" - звезда восьмиугольная.
Объединением каких двух многогранников он является? Что является их пересечением?

Ответ: Тетраэдров; октаэдр.
Какие боковые ребра должны быть у правильных пятиугольных пирамид, чтобы при добавлении их к граням додекаэдра с ребром a получился малый звездчатый додекаэдр?

Какие ребра должны быть у правильных треугольных пирамид, чтобы при удалении их из граней икосаэдра с ребром a получился большой додекаэдр?

Какие ребра должны быть у правильных треугольных пирамид, чтобы при добавлении их к граням икосаэдра с ребром a получился большой звездчатый додекаэдр?

Вершинами какого многогранника являются вершины большого звездчатого додекаэдра?

Как из большого додекаэдра можно получить многогранник, изображенный на рисунке?

Ответ: Операцией усечения.
Трехмерные модели однородных многогранников и их звездчатых форм
Здесь можно увидеть трехмерные модели всех известных однородных многогранников: выпуклых Платоновых и Архимедовых тел, тел Кеплера - Пуансо и полуправильных звездчатых многогранников. В таблице представлен полный список многогранников и их некоторые характеристики. Для каждой трехмерной модели предусмотрено несколько вариантов раскраски, имеется также возможность просмотра строения граней и вершин. В специальном разделе галереи можно бегло ознакомиться с обзорными изображениями моделей.
Для каждого однородного многогранника можно породить как в трехмерном калейдоскопе огромное множество звездчатых форм, внешне чрезвычайно привлекательных. Достаточно рассмотреть изображения звезд в галерее, а также примеры звездоформ икосаэдра и кубоктаэдра. Для более сложных многогранников звездчатые формы практически не известны; этот сайт практически впервые дает возможность их увидеть и изучить. Для вас доступны два пути поиска новых многогранников: выбор какой-либо уже представленной на сайте звездчатой формы (а всего их тут более миллиона), либо целенаправленная сборка нового многогранника из отсеков в режиме ручного редактирования звездчатых форм.
Привлекательный внешний вид и огромное разнообразие форм однородных многогранников и их звездчатых форм делают перспективным применение оных как декоративных элементов.
Вы можете сохранить на локальный диск любой многогранник для использования в собственных проектах, компьютерном дизайне и графике. Возможен экспорт трехмерных моделей в форматах 3DMAX (*.3ds), VRML (*.vrml), DirectX (*.x) и соответствующих анимированных изображений (*.jpg, *.avi, *.swf).
Вы можете создавать оригинальные электронные поздравительные открытки с изображениями многогранников. Достаточно выбрать самый красивый многогранник и подписать текст. Вашей открытке будет присвоен уникальный URL (интернет-ссылка), которую вы можете передать заинтересованным лицам. Новинка сезона - создание надписей прямо на гранях многогранника!
Многие великие и умные люди проявляли интерес к многогранникам. Во времена Пифагора учение о многогранниках было сакральным, тайной, доступной только избранным. В философской системе Платона важная роль отводилась правильным многогранникам. Архимед перечислил все полуправильные выпуклые многогранники. Кеплер придумал два звёздчатых правильных многогранника, затем Пуансо нашел ещё два, а Коши доказал: других правильных нет. Коксетер и другие только в середине 20 века перечислили остальные полуправильные невыпуклые многогранники. Ещё позднее удалось доказать, что список однородных многогранников полон.
Что касается звездчатых форм сложных многогранников, то они практически никому не известны. Возможно именно Вам посчастливится найти интересно устроенный или особенно красивый многогранник! Тогда в галерее среди достойнейших мужей вы сможете занять свое почетное место.

Ромбический додекаэдр - это зоноэдр . Его многогранный двойник - кубооктаэдр . Длинную диагональ каждой грани ровно ? 2 раза больше длины короткой диагонали, так что острые углы на каждой грани ( с мерой агссоз 1 / 3 ), или примерно 70,53 °.
Будучи двойственным к архимедову многограннику , ромбический додекаэдр является гранно-транзитивным , что означает, что группа симметрии твердого тела транзитивно действует на множестве граней. В элементарных терминах это означает, что для любых двух граней A и B существует вращение или отражение твердого тела, в результате чего оно занимает одну и ту же область пространства при перемещении грани A к грани B.
Ромбический додекаэдр можно рассматривать как выпуклую оболочку объединения вершин куба и октаэдра. 6 вершин, где встречаются 4 ромба, соответствуют вершинам октаэдра, а 8 вершин, в которых встречаются 3 ромба, соответствуют вершинам куба.
Ромбический додекаэдр является одним из девяти реберно-транзитивных выпуклых многогранников, остальные - это пять Платоновых тел , кубооктаэдр , икосододекаэдр и ромбический триаконтаэдр .
Ромбический додекаэдр можно использовать для мозаичного построения трехмерного пространства. Его можно сложить, чтобы заполнить пространство так же, как шестиугольники заполняют плоскость.
Этот многогранник в пространстве заполнения тесселяции можно рассматривать как Вороную тесселяцию в гранецентрированной кубической решетке . Это зона Бриллюэна объемно-центрированных кубических (ОЦК) кристаллов. Некоторые минералы, такие как гранат, образуют ромбический додекаэдрический кристалл . Как отметил Иоганн Кеплер в своей книге о снежинках 1611 года ( Strena seu de Nive Sexangula ), медоносные пчелы используют геометрию ромбических додекаэдров для формирования сот из мозаики ячеек, каждая из которых представляет собой шестиугольную призму, покрытую половиной ромбического додекаэдра. Ромбический додекаэдр также появляется в элементарных ячейкахалмаз и алмазоиды . В этих случаях четыре вершины (чередующиеся тройные) отсутствуют, но химические связи лежат на остальных ребрах. [1]
График ромбического додекаэдра негамильтонов .
Ромбический додекаэдр можно разрезать центром на 4 тригональных трапеции . Эти ромбоэдры являются ячейками треугольных трапециевидных сот . Это аналогично рассечению правильного шестиугольника, разрезанного на ромбы и выложенного на плоскости ромбиком .
В коллекциях Лувра есть матрица в форме ромбического додекадрона, датируемая Птолемеевым Египтом . Грани начертаны греческими буквами, представляющими числа от 1 до 12: A V G D E Z 6 I TH I IA IV. Функция матрицы неизвестна. [2]
Ромбически рассеченный шестиугольник
На этой анимации показано построение ромбического додекаэдра из куба путем инвертирования пирамид с центральными гранями куба.
Если длина край ромбического додекаэдра , то радиус из вписанного шара ( касательной к каждой из граней ромбического додекаэдра в) является
а радиус средней сферы равен
Площадь A и объем V ромбического додекаэдра с длиной ребра a равны:
Ромбического додекаэдра имеет четыре специальные ортогональные проекции вдоль его оси симметрии , сосредоточенных на лице, кромки, и два типа вершин, в три раза и в четыре раза. Последние два соответствуют самолетам Кокстера B 2 и A 2 .
| Проективная симметрия | [4] | [6] | [2] | [2] |
|---|---|---|---|---|
| Ромбический додекаэдр | ||||
| Кубооктаэдр (двойственный) |
Вариации пиритоэдра между кубом и ромбическим додекаэдром | Расширение ромбического додекаэдра |
Восемь вершин, где три грани встречаются под тупыми углами, имеют декартовы координаты :
Координаты шести вершин, где четыре грани встречаются под острыми углами:
(± 2, 0, 0), (0, ± 2, 0) и (0, 0, ± 2)
Ромбический додекаэдр можно рассматривать как вырожденный предельный случай пиритоэдра с перестановкой координат (± 1, ± 1, ± 1) и (0, 1 + h , 1 - h 2 ) с параметром h = 1.
Ромбического додекаэдра является параллелоэдр , А пространство заполнения полиэдр , dodecahedrille , будучи двойственной к tetroctahedrille или половину кубического соты , и описываются двумя схемами Кокстера : и . При симметрии D 3d его можно рассматривать как удлиненный тригональный трапецоэдр .
Ромбический додекаэдр может разбивать пространство на мозаику с помощью своих трансляционных копий . То же самое и со звездчатым ромбическим додекаэдром . | Ромбический додекаэдр может быть построен с 4 - мя наборы параллельных ребер. |
Другие конструкции симметрии ромбического додекаэдра также заполняют пространство, и как параллелоэдры они похожи на вариации заполняющих пространство усеченных октаэдров . [3]
Например, с 4 квадратными гранями и ромбическими гранями под углом 60 градусов и двугранной симметрией D 4h , порядок 16. Его можно рассматривать как кубооктаэдр с квадратными пирамидами, увеличенными сверху и снизу.
Сеть | Координаты (0, 0, ± 2) (± 1, ± 1, 0) (± 1, 0, ± 1) (0, ± 1, ± 1) |
Додекаэдр Билинского с краями и передними гранями, окрашенными в соответствии с их положением симметрии. | Додекаэдр Билинского, раскрашенный параллельными гранями |
В 1960 году Станко Билински открыл второй ромбический додекаэдр с 12 конгруэнтными гранями ромба, додекаэдр Билински . Он имеет ту же топологию, но другую геометрию. Ромбические грани в этой форме имеют золотое сечение . [4] [5]
| Однородные октаэдрические многогранники | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия : [4,3], (* 432) | [4,3] + (432) | [1 + , 4,3] = [3,3] (* 332) | [3 + , 4] (3 * 2) | |||||||
| т | г г | т т | | rr s 2 | tr | sr | ч | ч 2 т | с с | |
| знак равно | знак равно | знак равно | знак равно или же | знак равно или же | знак равно | |||||
| Двойники к однородным многогранникам | ||||||||||
| V4 3 | V3.8 2 | В (3,4) 2 | V4.6 2 | V3 4 | V3.4 3 | V4.6.8 | V3 4 .4 | V3 3 | V3.6 2 | V3 5 |
При проецировании на сферу (см. Справа) можно увидеть, что ребра составляют ребра двух тетраэдров, расположенных в их двойных положениях (стелла octangula). Эта тенденция продолжается с дельтоидальным икоситетраэдром и дельтоидальным гексеконтаэдром для двойных пар других правильных многогранников (наряду с треугольной бипирамидой, если следует учитывать неправильные мозаики), давая этой форме альтернативное систематическое название дельтоидного додекаэдра .
| Симметрия * n 32 [n, 3] | Сферический | Евклид. | Компактная гиперб. | Paraco. | ||||
|---|---|---|---|---|---|---|---|---|
| * 232 [2,3] | * 332 [3,3] | * 432 [4,3] | * 532 [5,3] | * 632 [6,3] | * 732 [7,3] | * 832 [8,3] . | * ?32 [?, 3] | |
| Рисунок Config. | V3.4.2.4 | V3.4.3.4 | V3.4.4.4 | V3.4.5.4 | V3.4.6.4 | V3.4.7.4 | V3.4.8.4 | V3.4.?.4 |
Этот многогранник является частью последовательности ромбических многогранников и мозаик с симметрией [ n , 3] группы Кокстера . Куб можно рассматривать как ромбический шестигранник, в котором ромбы представляют собой квадраты.
| Изменения симметрии двойственных квазирегулярных мозаик: V (3.n) 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| * n32 | Сферический | Евклидово | Гиперболический | ||||||||
| * 332 | * 432 | * 532 | * 632 | * 732 | * 832 . | * ?32 | |||||
| Плитка | |||||||||||
| Конф. | В (3,3) 2 | В (3,4) 2 | В (3,5) 2 | В (3,6) 2 | В (3,7) 2 | V (3.8) 2 | V (3.?) 2 | ||||
| * n 42 изменения симметрии квазирегулярных двойственных мозаик: V (4.n) 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия * 4n2 [n, 4] | Сферический | Евклидово | Компактный гиперболический | Паракомпакт | Некомпактный | ||||||
| * 342 [3,4] | * 442 [4,4] | * 542 [5,4] | * 642 [6,4] | * 742 [7,4] | * 842 [8,4] . | * ?42 [?, 4] | [ip / l, 4] | ||||
| Кафельная
Точно так же это относится к бесконечной серии мозаик с конфигурациями граней V3.2 n .3.2 n , первая в евклидовой плоскости, а остальные - в гиперболической плоскости.
Как и многие выпуклые многогранники, ромбический додекаэдр можно сделать звездчатым, если удлинить грани или ребра до тех пор, пока они не встретятся, чтобы сформировать новый многогранник. Несколько таких звездочек были описаны Дорманом Люком. [9] На этой анимации показано построение звездчатого ромбического додекаэдра путем переворота пирамид с центральной гранью ромбического додекаэдра. Первая звездчатая форма, которую часто называют просто звездчатым ромбическим додекаэдром , хорошо известна. Его можно рассматривать как ромбический додекаэдр с каждой гранью, увеличенной путем присоединения к нему пирамиды с ромбической основой, с такой высотой пирамиды, что стороны лежат в плоскостях граней соседних граней: 
Читайте также: | |||||||||||
 webdonsk.ru
webdonsk.ru