Как сделать шаблон параболы по алгебре 8 класс

Добавил пользователь Евгений Кузнецов
Обновлено: 09.09.2024

Рассмотрим уравнение параболы с вершиной в произвольной точке.

Умножим числитель на величину, обратную знаменателю .

Подставляем значения , , и в уравнение канонического вида .

Так как значение положительно, ветви параболы направлены вверх.

Найдем расстояние от вершины до фокуса параболы с помощью следующей формулы.

Фокус параболы может быть найден с помощью прибавления к координате Y вершины параболы, ветви которой направлены вверх или вниз.

Подставим известные значения , и в формулу и упростим.

Найдем ось симметрии, определив прямую, проходящую через вершину и фокус.

Директрисой параболы является горизонтальная прямая, определяемая вычитанием из координаты Y вершины параболы, ветви которой направлены вверх или вниз.

Цель: продолжить формирование умения строить график функции у = а (х – т) 2 + п, используя при этом шаблоны парабол.

I. Организационный момент.

II. Устная работа.

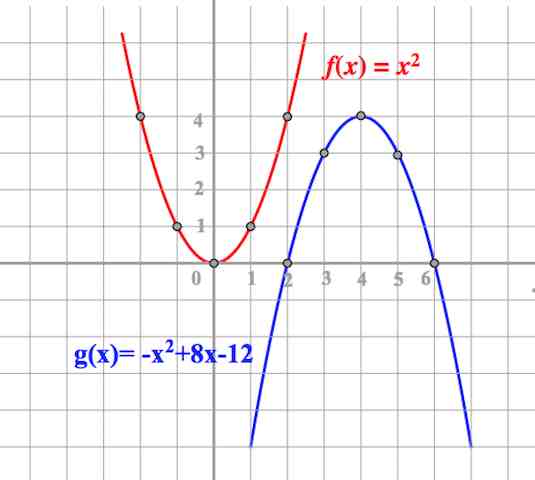
Для каждого из графиков, изображенных на рисунке, найдите соответствующую функцию:

а) у = ; г) у = х 2 + 1;

б) у = –2х 2 + 1; д) у = ;

в) у = (х – 1) 2 – 2; е) у = (х + 1) 2 – 2.

III. Формирование умений и навыков.

Учащиеся выполняют з а д а н и я двух групп:

– построение графика функции у = а (х – т) 2 + п с использованием шаблонов;

– построение графика функции у = а (х – т) 2 + п с помощью преобразований.

2. Используя шаблон параболы у = 2х 2 , постройте график функций:

а) у = 2 (х + 1) 2 – 4; б) у = –2 (х – 3) 2 + 2.

3. Используя шаблон параболы у = х 2 , постройте график функции:

а) у = ;

б) у = .

1. Постройте графики функции:

а) у = ;

б) у = –3(х – 1) 2 + 4;

в) у =

2. Задайте формулой функцию, график которой изображен на рисунке:

IV. Проверочная работа.

В а р и а н т 1

1. Изобразите схематически графики функций:

а) у = –(х – 3) 2 ;

б) у = х 2 + 1;

в) у = 2 (х + 1) 2 – 3.

2. Используя шаблон параболы у = х 2 , постройте график функций:

а) у = (х + 2) 2 – 3;

б) у = –(х – 1) 2 + 4.

3*. Задайте формулой функцию, график которой изображен на рисунке:

В а р и а н т 2

1. Изобразите схематически графики функций:

а) у = –2х 2 + 3;

б) у = (х + 2) 2 ;

в) у = –(х – 1) 2 – 2.

2. Используя шаблон параболы у = х 2 , постройте графики функций:

а) у = (х – 3) 2 – 2;

б) у = –(х + 1) 2 + 5.

3*. Задайте формулой функцию, график которой изображен на рисунке:

V. Итоги урока.

В о п р о с ы у ч а щ и м с я:

– Что является графиком функции у = а (х – т) 2 + п?

– Как может быть получен график функции у = а (х – т) 2 + п из графика функции у = ах 2 ?

– Какие координаты имеют вершины парабол:

у = 2 (х – 3) 2 + 4, у = (х + 1) 2 – 5?

Домашнее задание:

2. Постройте графики функций:

а) у = –2 (х – 1) 2 + 3; б) у = (х + 2) 2 – 4.

В а р и а н т 1

1. Изобразите схематически графики функций:

а) у = –(х – 3) 2 ;

б) у = х 2 + 1;

в) у = 2 (х + 1) 2 – 3.

2. Используя шаблон параболы у = х 2 , постройте график функций:

а) у = (х + 2) 2 – 3;

б) у = –(х – 1) 2 + 4.

3*. Задайте формулой функцию, график которой изображен на рисунке:

В а р и а н т 2

1. Изобразите схематически графики функций:

а) у = –2х 2 + 3;

б) у = (х + 2) 2 ;

в) у = –(х – 1) 2 – 2.

2. Используя шаблон параболы у = х 2 , постройте графики функций:

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где называется квадратичной функцией.

В уравнении квадратичной функции:

a - старший коэффициент

b - второй коэффициент

с - свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками - это, так называемые "базовые точки". Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.

График функции имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0 , то ветви параболы напрaвлены вверх .

Если старший коэффициент a , то ветви параболы напрaвлены вниз .

Второй параметр для построения графика функции - значения х, в которых функция равна нулю, или нули функции. На графике нули функции - это точки пересечения графика функции с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции нужно решить квадратное уравнение .

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:

2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:

3 . Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:

>/" />
, >/" />

Если ,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции - координаты вершины параболы:

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции - точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции

1. Направление ветвей параболы.

Так как ,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена

=7" />

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение:

/4=1" />
, /4=-2,5" />

3. Координаты вершины параболы:

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2 . Уравнение квадратичной функции имеет вид - в этом уравнении - координаты вершины параболы

или в уравнении квадратичной функции , и второй коэффициент - четное число.

Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

сначала построить график функции ,
затем одинаты всех точек графика умножить на 2,
затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции . В уравнении этой функции , и второй коэффициент - четное число.

Выделим в уравнении функции полный квадрат:

Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3 . Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции - точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на координатную плоскость и построим график:

График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
- ширины графика функции от значения коэффициента ,
- сдвига графика функции вдоль оси от значения ,

- сдвига графика функции вдоль оси от значения
- направления ветвей параболы от знака коэффициента
- координат вершины параболы от значений и :

И.В. Фельдман, репетитор по математике.

Для построения заполняем таблицу, подставляя значения x в формулу:

Отмечаем точки (0;0); (1;1); (-1;1) и т.д. на координатной плоскости (чем с меньшим шагом мы берем значения х ( в данном случае шаг 1 ), и чем больше берем значений х, тем плавнее будет кривая), получаем параболу:

Нетрудно заметить, что если мы возьмем случай , , , то есть , то мы получим параболу, симметричную относительно оси (ох). Убедиться в этом несложно, заполнив аналогичную таблицу:

Что же будет, если мы будем брать , , ? Как изменится поведение параболы? При парабола изменит форму, она “похудеет” по сравнению с параболой (не верите – заполните соответствующую таблицу – и убедитесь сами):

На первой картинке (см. выше) хорошо видно, что точки из таблицы для параболы (1;1), (-1;1) трансформировались в точки (1;4), (1;-4), то есть при тех же значениях ордината каждой точки умножилась на 4. Это произойдет со всеми ключевыми точками исходной таблицы. Аналогично рассуждаем в случаях картинок 2 и 3.

1) Знак коэффициента отвечает за направление ветвей. При ветви направлены вверх, при — вниз.

2) Абсолютная величина коэффициента (модуля) отвечает за “расширение”, “сжатие” параболы. Чем больше , тем у’же парабола, чем меньше |a|, тем шире парабола.

Теперь давайте введем в игру (то есть рассматриваем случай, когда ), будем рассматривать параболы вида . Нетрудно догадаться (вы всегда можете обратиться к таблице), что будет происходить смещение параболы вдоль оси вверх или вниз в зависимости от знака :

Когда же парабола “оторвется” от оси и будет, наконец, “гулять” по всей координатной плоскости? Когда перестанет быть равным .

Здесь для построения параболы нам понадобится формула для вычисления вершины: , .

Так вот в этой точке (как в точке (0;0) новой системы координат) мы будем строить параболу , что уже нам по силам. Если имеем дело со случаем , то от вершины откладываем один единичный отрезок вправо, один вверх, – полученная точка – наша (аналогично шаг влево, шаг вверх – наша точка); если имеем дело с , например, то от вершины откладываем один единичный отрезок вправо, два – вверх и т.д.

Например, вершина параболы :

, . Теперь главное уяснить, что в этой вершине мы будем строить параболу по шаблону параболы , ведь в нашем случае.

При построении параболы после нахождения координат вершины очень удобно учитывать следующие моменты:

1) парабола обязательно пройдет через точку . Действительно, подставив в формулу x=0, получим, что . То есть ордината точки пересечения параболы с осью (оу), это . В нашем примере (выше), парабола пересекает ось ординат в точке , так как .

2) осью симметрии параболы является прямая , поэтому все точки параболы будут симметричны относительно нее. В нашем примере, мы сразу берем точку (0; -2) и строим ей симметричную относительно оси симметрии параболы, получим точку (4; -2), через которую будет проходить парабола.

3) Приравнивая к , мы узнаем точки пересечения параболы с осью (ох). Для этого решаем уравнение . В зависимости от дискриминанта, будем получать одну (, ), две (, ) или нИсколько () точек пересечения с осью (ох) . В предыдущем примере у нас корень из дискриминанта – не целое число, при построении нам особо нет смысла находить корни, но мы видим четко, что две точки пересечения с осью (ох) у нас будут (так как ), хотя, в общем, это видно и без дискриминанта.

Итак, давайте выработаем

Алгоритм для построения параболы, если она задана в виде

1) определяем направление ветвей ( а>0 – вверх, a

2) находим координаты вершины параболы по формуле , .

3) находим точку пересечения параболы с осью (оу) по свободному члену , строим точку, симметричную данной относительно оси симметрии параболы (надо заметить, бывает, что эту точку невыгодно отмечать, например, потому, что значение велико… пропускаем этот пункт…)

4) В найденной точке – вершине параболы (как в точке (0;0) новой системы координат) строим параболу . Если , то парабола становится у’же по сравнению с , если , то парабола расширяется по сравнению с

5) Находим точки пересечения параболы с осью (оу) (если они еще сами “не всплыли”), решая уравнение

Замечание 1. Если же парабола изначально нам задана в виде , где – некоторые числа (например, ), то построить ее будет еще легче, потому что нам уже заданы координаты вершины . Почему?

Возьмем квадратный трехчлен и выделим в нем полный квадрат: Посмотрите, вот мы и получили, что , . Мы с вами ранее называли вершину параболы , то есть теперь , .

Например, . Отмечаем на плоскости вершину параболы , понимаем, что ветви направлены вниз, парабола расширена (относительно ). То есть выполняем пункты 1; 3; 4; 5 из алгоритма построения параболы (см. выше).

Замечание 2. Если парабола задана в виде, подобном этому (то есть представлен в виде произведения двух линейных множителей), то нам сразу видны точки пересечения параболы с осью (ох). В данном случае – (0;0) и (4;0). В остальном же действуем согласно алгоритму, раскрыв скобки.

Читайте также: