Как сделать смешанное произведение векторов

Добавил пользователь Евгений Кузнецов
Обновлено: 28.08.2024

Данный онлайн калькулятор вычисляет смешанное произведение векторов. Дается подробное решение. Для вычисления смешанного произведения векторов выберите способ представления векторов (по координатам или по двум точкам) введите данные в ячейки и нажимайте на кнопку "Вычислить."

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Смешанное произведение векторов (теория)

Смешанное произведение трех векторов это число, которое получается при скалярном произведении результата векторного произведения первых двух векторов на третьий вектор. Другими словами, если заданы три вектора a, b и c, то для получения смешанного произведения этих векторов, сначала векторно умножаются первые два вектора и полученный вектор [ab] скалярно умножается на вектор c.

Смешанное произведение трех векторов a, b и c обозначается так: abc или так (a,b,c). Тогда можно записать:

Прежде чем сформулировать теорему, представляющую геометрический смысл смешанного произведения, ознакомьтесь с понятиями правая тройка, левая тройка, правая система координат, левая система координат (определения 2, 2' и 3 на странице векторное произведение векторов онлайн).

Для определенности, в дальнейшем мы будем рассматривать только правые системы координат.

Теорема 1. Смешанное произведение векторов ([ab],c) равно объему параллелипеда, построенного на приведенных к общему началу векторах a, b, c, взятому со знаком плюс, если тройка a, b, c правая, и со знаком минус, если тройка a, b, c левая. Если векторы a, b, c компланарны, то ([ab],c) равно нулю.

Следствие 1. Имеет место следующее равенство:

Для доказательства следствия заметим, что из переместительного свойства скалярного произведения имеем:

Следовательно нам достаточно доказать, что

Из выражения (3) видно, что левая и правая часть равны объему параллелипеда. Но и знаки правой и левой частей совпадают, так как тройки векторов abc и bca имеют одинаковую ориентацию.

Доказанное равенство (1) позволяет записать смешанное произведение трех векторов a, b, c просто в виде abc, не указывая, какие именно два вектора перемножаются векторно первые два или последние два.

Следствие 2. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.

Доказательство вытекает из теоремы 1. Действительно, если векторы компланарны, то смешанное произведение этих векторов равно нулю. Обратное, если смешанное произведение равно нулю, то из теоремы 1 вытекает компланарность этих векторов (так как объем параллелипеда, построенного на приведенных к общему началу векторах равно нулю).

Следствие 3. Смешанное произведение трех векторов, два из которых совпадают, равно нулю.

Действительно. Если два вектора из трех совпадают, то они компланарны. Следовательно, смешанное произведение этих векторов равно нулю.

Смешанное произведение векторов в декартовых координатах

Теорема 2. Пусть три вектора a, b и c определены своими декартовыми прямоугольными координатами

a=x₁, y₁, z₁>, b=x₂, y₂, z₂>, c=x₃, y₃, z₃>.

Тогда смешанное произведение abc равняется определителю, строки которого соответственно равны координатам перемножаемых векторов:

Доказательство. Смешанное произведение abc равно скалярному произведению векторов [ab] и c. Векторное произведение векторов [ab] в декартовых координатах вычисляется формулой (подробнее смотрите на странице векторное произведение векторов онлайн):

[ab]=y₁z₂-y₂z₁, z₁x₂-z₂x₁, x₁y₂-x₂y₁>.

Тогда скалярное произведение векторов [ab] и c можно записать так:

abc=([ab],c)=x₃(y₁z₂-y₂z₁)+ y₃(z₁x₂-z₂x₁)+ z₃(x₁y₂-x₂y₁).

(5)

Последнее выражение можно записать, используя определители второго порядка:

(6)

Формулы (6) и (4) эквивалентны, так как (6) является разложением определителя (4) по третьей строке.

Следствие 3. Для компланарности трех векторов

a=x₁, y₁, z₁>, b=x₂, y₂, z₂>, c=x₃, y₃, z₃>.

необходимо и достаточно равенство нулю определителя, строки которой заполнены координатами этих векторов, т.е:

Для доказательства следствия достаточно рассмотреть формулу (4) и следствие 2.

Смешанное произведение векторов на примерах

Пример 1. Найти смешанное произведение векторов abс, где

Для вычисления смешанного произведения векторов a, b, c составим матрицу, строки которой образуются векторами a, b, c:

Смешанное произведение векторов a, b, c равен определителю матрицы L. Вычислим определитель матрицы L, разложив определитель по строке 1:

Смешанное произведение векторов a, b, c равен :

Пример 2. Найти смешанное произведение векторов abс, где

Начальная точка вектора a:

Конечная точка вектора a:

Начальная точка вектора c:

Конечная точка вектора c:

Переместим вектор a на начало координат. Для этого вычтем из соответствующих координат конечной точки B координаты начальной точки A:

Переместим вектор c на начало координат. Для этого вычтем из соответствующих координат конечной точки F координаты начальной точки E:

Для того чтобы мы могли ввести понятие смешанного произведения векторов, нужно сначала вспомнить понятия скалярного и векторного произведений этих векторов.

Скалярным произведением двух векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.

Математически это может выглядеть следующим образом:

Также, помимо того, как из самого определения 1, для нахождения скалярного произведения можно пользоваться следующей теоремой.

Скалярное произведение двух данных векторов $\overline$ и $\overline$ равняется сумме произведений их соответствующих координат.

Математически выглядит следующим образом

$\overline\overline=a_1 a_2+v_1 v_2$

Обозначение: $\overline\cdot \overline$.

Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.

Математически это выглядит следующим образом:

$|\overlineх\overline|=|\overline||\overline|sin?(\overline,\overline)$
$\overlineх\overline?\overline$, $\overlineх\overline?\overline$
$(\overlineх\overline,\overline,\overline)$ и $(\overline,\overline,\overline)$ одинаково ориентированы (рис. 1)

Готовые работы на аналогичную тему

Понятие смешанного произведения векторов

Смешанным произведением векторов $\overline$, $\overline$ и $\overline$ будем называть такой скаляр (или число), которое будет равняться скалярному произведению первого вектора $\overline$ на вектор векторного произведения $\overlineх\overline$ двух других векторов.

Математически это выглядит следующим образом:

Очевидно, что смешанное произведение будет равняться нулю в двух случаях:

Если длина одного или нескольких векторов равняется нулю.
Если эти векторы будут являться компланарными.

Найти значение смешанного произведения векторов $\overline$, $\overline$ и $\overline$, которые имеют координаты $(0,0,5)$, $(0,4,0)$ и $(3,0,0)$, соответственно.

Из определений 1, и 3 будем получать

Изобразим эти векторы в декартовом координатном пространстве (рис. 2):

Найдем вначале длину вектора векторного произведения векторов $\overline$ и $\overline$

Видим, что эти векторы лежат на осях $Ox$ и $Oy$, соответственно. Следовательно, угол между ними будет равняться $90^0$. Найдем длины этих векторов:

Тогда, по определению 2, получим

$|\overlineх\overline|=|\overline||\overline|sin90^\circ=4\cdot 3\cdot 1=12$

Из 3 части определения 2 очевидно, что вектор $\overlineх\overline$ принадлежит оси $Oz$ и направлен в туже сторону, что и сама ось, следовательно, угол между векторами $\overline$ и $\overlineх\overline$ равняется $0^\circ$.

Длина вектора $\overline$

Вычисление смешанного произведения по координатам векторов

Из определения 1 сразу же вытекает и способ нахождения смешанного произведения для трех данных векторов. Но существует еще способ нахождения с помощью координат данных нам векторов.

Пусть нам даны векторы $\overline$, $\overline$ и $\overline$, которые будут иметь координаты $(a_1,a_2,a_3)$, $(v_1,v_2,v_3)$ и $(g_1,g_2,g_3)$, соответственно. Тогда значение смешанного произведения можно найти по следующей формуле:

$\overlineх\overline=a_1 v_2 g_3+a_3 v_1 g_2+a_2 v_3 g_1-a_3 v_2 g_1-a_2 v_1 g_3-a_1 v_3 g_2$

Найти значение смешанного произведения векторов $\overline$, $\overline$ и $\overline$ с координатами $(1,1,0)$, $(0,3,3)$ и $(-1,2,6)$.

Воспользуемся формулой, приведенной выше. Получим

Свойства смешанного произведения векторов

Для произвольных четырех векторов $\overline, $\overline$, $\overline$ и $\overline$, а также $r?R$ справедливы следующие свойства: справедливы следующие свойства:

1) При перестановке местами знаков произведений в смешанном произведении можно менять между собой

$(\overline,\overline,\overline)=\overline\cdot (\overlineх\overline)=(\overlineх\overline)\cdot \overline$

Смешанным произведением векторов называется число , равное скалярному произведению вектора .

Геометрические свойства смешанного произведения

1. Модуль смешанного произведения некомпланарных векторов равен объему параллелепипеда, построенного на этих векторах. Произведение положительно, если тройка векторов — правая, и отрицательно, если тройка — левая, и наоборот.

2. Смешанное произведение равно нулю тогда и только тогда, когда векторы компланарны:

Докажем первое свойство. Найдем по определению смешанное произведение: , где — угол между векторами . Модуль векторного произведения (по геометрическому свойству 1) равен площади параллелограмма, построенного на векторах . Поэтому . Алгебраическое значение длины проекции вектора , равно по модулю высоте параллелепипеда, построенного на векторах (рис. 1.47). Поэтому модуль смешанного произведения равен объему этого параллелепипеда:

Знак смешанного произведения определяется знаком косинуса угла . Если тройка правая, то и смешанное произведение положительно. Если же тройка левая, то и смешанное произведение отрицательно.

Докажем второе свойство. Равенство возможно в трех случаях: или (т.е. ),или (т.е. вектор компланарны (см. разд. 1.1).

Алгебраические свойства смешанного произведения

1. При перестановке двух множителей смешанное произведение изменяет знак на противоположный:

При циклической (круговой) перестановке множителей смешанное произведение не изменяется:

2. Смешанное произведение линейно по любому множителю.

Первое свойство следует из геометрического свойства 1 и свойств ориентации троек векторов (см. разд. 1.9), поскольку от перестановки двух множителей модуль смешанного произведения не изменяется, а меняется только ориентация тройки. При циклической перестановке векторов ориентация тройки не изменяется.

Второе свойство следует из линейности скалярного произведения и свойства 1.

Пример 1.21. Объем параллелепипеда, построенного на векторах , равен

Решение. Используя алгебраические и геометрические свойства, найдем смешанное произведение

а затем его модуль . По первому геометрическому свойству смешанного произведения искомый объем равен .

Формула вычисления смешанного произведения

Теорема 1.9 (формула вычисления смешанного произведения). Если векторы в правом ортонормированном базисе имеют координаты ; ; соответственно, то смешанное произведение этих векторов находится по формуле

В самом деле, учитывая (1.10) и (1.15), по определению находим:

что и требовалось доказать.

1. Используя свойства смешанного произведения, можно доказать линейность векторного произведения по первому множителю (см. п.1 замечаний 1.12 в разд.1.15):

Для этого найдем скалярное произведение вектора в левой части равенства и единичного вектора стандартного базиса. Учитывая линейность смешанного произведения по второму множителю, получаем

т.е. абсцисса вектора, стоящего в левой части доказываемого равенства равна абсциссе вектора в правой его части (см. пункт З замечаний 1.10). Аналогично доказываем, что ординаты, а также и аппликаты, векторов в обеих частях равенства соответственно равны. Следовательно, это равные векторы, так как их координаты относительно стандартного базиса совпадают.

2. Из первого алгебраического свойства смешанного произведения и коммутативности скалярного произведения следует, что

т.е. . Последнее равенство можно взять в качестве эквивалентного определения смешанного произведения.

3. Если тройка векторов является базисом пространства, то тройка векторов

образует взаимный базис.

В самом деле, указанный вектор по определению векторного произведения ортогонален векторам и ,т.е. и , а скалярное произведение равно единице, так как . Поэтому вектор содержится во взаимном базисе. Аналогичные рассуждения проводятся относительно векторов и . Поэтому базисы и взаимные.

4. Если — координатные столбцы векторов в стандартном базисе, то их смешанное произведение находится по формуле

Пример 1.22. Параллелепипед построен на векторах (рис.1.48). Требуется найти:

а) смешанное произведение , а также ориентацию тройки ;

б) объем треугольной пирамиды ;

в) высоту параллелепипеда (расстояние между плоскостями оснований ).

Решение. а) Смешанное произведение находим по формуле (1.17):

Поскольку произведение отрицательно, то тройка векторов — левая (см. первое геометрическое свойство смешанного произведения).

Для нахождения смешанного произведения можно использовать матричную запись формулы (1.17) (см. пункт 4 замечаний 1.13). Векторам ,

По формуле пункт 4 замечаний 1.13 получаем

б) Объем составляет шестую часть объема параллелепипеда. Действительно, их высоты совпадают, а площадь основания пирамиды составляет половину площади параллелограмма . Поскольку , то

в) Высоту параллелепипеда найдем по формуле , где — площадь параллелограмма и (см. пример 1.20), то .

Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах $\overline$, $\overline$ и $\overline$ равен модулю смешанного произведения этих векторов:

Объем пирамиды, построенной на этой тройке векторов равен

Свойства смешанного произведения:

Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

В качестве обозначения действия используют следующее выражение:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Можно отметить сходство скалярного и векторного произведений векторов, так как действия совершаются в том и другом случае с двумя векторами. Однако в результате скалярного умножения получается числовая величина, а векторного — вектор.

В качестве доказательства результат векторного произведения можно записать, таким образом:

Смешанным произведением векторов называют умножение трех векторов.

Обозначить действие можно следующим образом:

Геометрический смысл смешанного произведения векторов заключается в том, что объем параллелепипеда, который построен с помощью трех векторов $\mathbf, \mathbf, \mathbf$ представляет собой модуль смешанного произведения этих векторов:

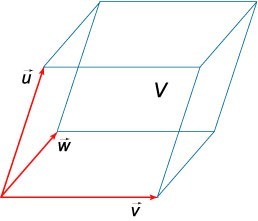
Пирамида, которая построена на трех векторах $\mathbf, \mathbf, \mathbf$ обладает объемом, равным:

$V = \large\frac\normalsize \left| <\left( <\mathbf,\mathbf,\mathbf> \right)> \right| = \large\frac\normalsize \left| <\mathbf\cdot \left( <\mathbf\times \mathbf> \right)> \right|$

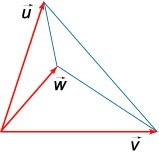
Формула вычисления смешанного произведения трех векторов

В качестве формулы для нахождения смешанного произведения трех векторов $\mathbf, \mathbf \ и \ \mathbf$ используют скалярное произведение вектора $\mathbf$ на векторное произведение векторов $\mathbf \ и \ \mathbf$

Выражение можно записать следующим образом:

$\left( <\mathbf,\mathbf,\mathbf> \right) = \mathbf \cdot \left( <\mathbf\times \mathbf> \right) = \mathbf \cdot \left( <\mathbf\times \mathbf> \right) = \mathbf \cdot \left( <\mathbf\times \mathbf> \right)$

Свойства, особенности умножения в системе координат

При выполнении действий со смешанным произведением векторов целесообразно использовать справедливые закономерности. Их применение упрощает решение задач. К таким свойствам относят:

$k\mathbf \cdot \left( <\mathbf\times \mathbf> \right) = k\left( <\mathbf,\mathbf,\mathbf> \right)$

При рассмотрении смешанного произведения в системе координат можно записать следующее выражение:

Векторы в пространстве \mathbf, \mathbf и \mathbf называют линейно зависимыми или компланарными в том случае, когда их смешанное произведение соответствует нулевому значению.

В таком случае, один из указанных векторов можно определить с помощью двух других векторов:

$\mathbf = \lambda \mathbf + \mu \mathbf$

В данной форме выражении \lambda, \mu являются некоторыми действительными числами.

Линейно независимые векторы $\mathbf, \mathbf \ и \ \mathbf$ представляют собой такие векторы, следствием смешанного произведения которых является значение, отличное от нуля.

Двойное векторное произведение трех векторов $ \mathbf, \mathbf \ и \ \mathbf$ представляет собой векторное произведение в виде формулы:

$\mathbf \times \left( <\mathbf\times \mathbf> \right) = \left( <\mathbf\cdot \mathbf> \right)\mathbf - \left( <\mathbf\cdot \mathbf> \right)\mathbf = \left| > \mathbf & \mathbf\\ <\left( <\mathbf\cdot \mathbf> \right)> & <\left( <\mathbf\cdot \mathbf> \right)> \end> \right| $

Разбор типовых задач, примеры решения

Требуется определить: значение смешанного произведения векторов, объемы параллелепипеда и тетраэдра, которые построены на основе заданных векторов.

Необходимо воспользоваться формулой смешанного произведения

В данном случае определитель раскрывают, ориентируясь на первую колонку.

Объем параллелепипеда, который построен на рассматриваемых в условии задачи векторах, можно найти с помощью модулю смешанного произведения этих векторов:

В случае определения объема тетраэдра следует использовать выражение:

Требуется определить объем треугольной пирамиды. Ее вершины заданы, таким образом:

Читайте также: