Как сделать сечение четырехугольной призмы
Задача: Точки А, В, С - точки на разных ребрах четырехугольной призмы. Найдем сечение призмы плоскостью ABC.
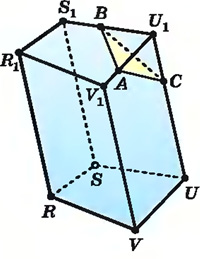
Построение искомого сечения зависит от того, на каких ребрах призмы лежат точки А, В, С. Наиболее просто строить сечение в том случае, когда точки А, В, С лежат на ребрах, выходящих из одной вершины. Искомое сечение в этом случае — треугольник: АВС.
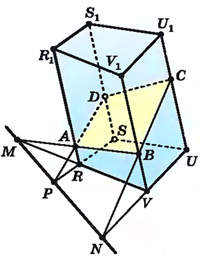
Если точки А, В, С расположены так, как изображено на рисунке, то строить сечение сложнее. Здесь сначала построим след секущей плоскости АВС на плоскости нижнего основания. Для этого найдем точки М и N пересечения прямых АВ и ВС, которые лежат в секущей плоскости, с плоскостью RSUV: М — точка пересечения прямых АВ и RV, N — точка пересечения прямых ВС и UV. Прямая MN — общая прямая секущей плоскости и плоскости нижнего основания.
Точка Р пересечения прямой RS со следом MN принадлежит и секущей плоскости, и плоскости грани RR1S1S. Учитывая, что этим двум плоскостям принадлежит и точка А, получаем, что прямая РА — след секущей плоскости на плоскости RR1S1S. Значит, плоскость АBС пересекает грань RR1S1S по отрезку AD, а грань UU1S1S — по отрезку CD. Искомым сечением является четырехугольник ABCD.
Видим, что новым элементом в этом решении по сравнению с задачей построить сечение треугольной пирамиды является построение следа секущей плоскости на плоскости основания.
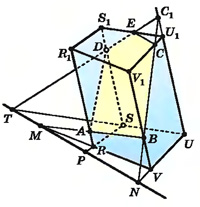
На рисунке показан случай, когда искомым сечением является пятиугольник. Здесь использована точка Сх пересечения ребра UU1с секущей плоскостью. Следы секущей плоскости на боковых гранях пирамиды строятся таре же, как и в предыдущем случае.
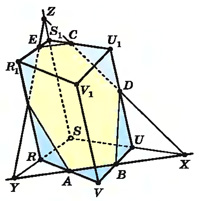
Рисунок показывает, что искомым сечением четырехугольной призмы может быть и шестиугольник. След АВ секущей плоскости на плоскости основания позволяет последовательно найти точки X и Y его пересечения с гранями SUU1S1 и RSS1R1, след ХС секущей плоскости на плоскости SUU1S1, точку Z пересечения ребра SS1 с секущей плоскостью и след ZY секущей плоскости на грани RSS1R1.
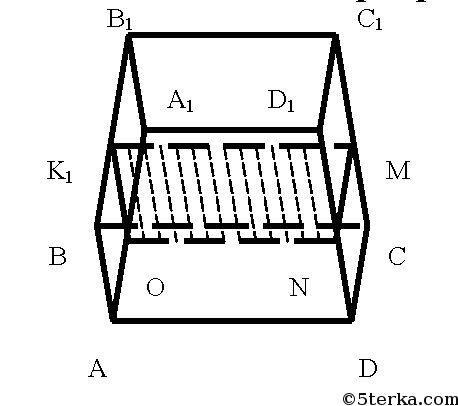
1) Точки K, M, N расположены так, что MN || DC и KM || MN. Тогда плоскость, проходящая через точки K, M и N параллельна плоскости грани ABCD, т.к. две пересекающие прямые KM и MN параллельны грани ABCD. Проведем прямую ON || AD. Тогда она будет принадлежать плоскости сечения. Так как иначе она пересекала бы и грань ABCD, то есть и AD, что неверно.
Тогда четырехугольник KMNO искомое сечение.
2) Точки K, M, N располагаются так, что КМ || ВС, но MN не параллельно DC. Тогда через точки M и N проведем прямую а, которая пересекает прямую DC в некоторой точке S.

Тогда S принадлежит сечению. Через точку S проведем прямую b || KM. Тогда b принадлежит сечению и b || BC, т.к. b || KM и КМ || ВС. Тогда АВ пересекает прямую b в некоторой точке X. Тогда Х принадлежит сечению.
А также можно соединить точи К и Х отрезком, который пересечет А1А в некоторой точке О. Тогда точка О тоже принадлежит сечению. А значит, четырехугольник OKMN это искомое сечение.

3) Когда точки К, M, N располагаются так, что MN не параллельно DC и KМ не параллельно MN. Тогда прямая MN пересечет прямую DC в некоторой точке F, прямая МК пересечет прямую ВС в некоторой точке X. Точки X и F принадлежат плоскости ABCD, а также искомому сечению, значит, плоскость ABCD и сечение пересекаются по прямой XF. Тогда прямая АВ, или прямая AD, или обе эти прямых пересекают прямую XF. Допустим АВ пересекает XF в точке S. Тогда точка S принадлежит и плоскости АА1В1В, а также сечению. Проведем прямую SK. Она пересечет ребро АА1 в точке О. Так что MNOK искомое сечение.
26 декабря, 2013 Анна Веселова


Здравствуйте! Сегодня мы коснемся такой темы, как сечение призмы плоскостью и построим развертку усеченной призмы в Компасе.
За основу возьмем 3 d модель призмы из урока 2 по 3d моделированию.
Последовательность построения чертежа усеченной призмы
1. Создаем чертеж, меняем формат на А3.
4. Проводим осевые линии.
5. От центра симметрии призмы откладываем расстояние до следа секущей плоскости. В нашем примере это 37 мм. Из полученной точки проводим след секущей плоскости Pv под углом 45?

6. Обозначаем точки пересечения секущей плоскости с ребрами призмы на фронтальной проекции призмы и по линиям связи находим эти точки на оставшихся проекциях. Таким образом, получаем искаженные фигуры сечения призмы плоскостью в проекциях.

7. Но нам необходимо знать, как выглядит натуральный вид сечения призмы или действительная величина контура сечения. Строим его.
Построение натурального вида сечения призмы
8. Для построения из каждой точки фронтальной проекции поднимаем перпендикуляры.
9. Переносим соответствующие размеры с горизонтальной проекции призмы на новую горизонтальную проекцию (т. к. натуральный вид сечения мы строим способом перемены плоскостей проекций).

Развертка усеченной призмы
10. Развертку усеченной призмы будем строить на одной линии координатными осями проекций призмы. Так будет меньше вспомогательных построений.

11. Сначала строим отрезок длиной, равной длине всех 6 ребер призмы, получается 120 мм.
12. Делим этот отрезок на 6 частей, нумеруем.
13. При помощи вспомогательных линий переносим высоты ребер усеченной призмы, соединяем вершины отрезков.
14. Действительную фигуру сечения переносим на развертку путем копирования (ctrl+выделяем левой кнопкой мыши), достраиваем нижнее основание призмы. Линии сгиба обозначаем специальной линией, она в Компасе называется – пунктир 2.
Строим изометрию усеченной призмы
15. Изометрию будем строить вручную, т. е. все операции построения в точности повторяют черчение аксонометрии на бумаге.
16. Проводим две вспомогательные линии под углами 30 и 150 градусов, строим изометрию нижнего основания – шестиугольник, нумеруем их.
17. Затем из каждой вершины шестиугольника поднимаем отрезки, высотой, равной высоте соответствующих отрезков на фронтальной проекции призмы. Соединяем точки. Изометрия готова.
18. Теперь остается только оформить чертеж в соответствии с требованиями и заполнить основную надпись.

Весь процесс создания чертежа усеченной призмы подробно рассмотрен в небольшом видеоуроке.

Теперь вы без труда построите сечение призмы плоскостью и развертку усеченной призмы.
а у параллелепипеда, в основании которого находится параллелограмм, диагонали только попарно равны: DF ? EC , т. к. DB ? CA .
Диагональное сечение призмы — это сечение плоскостью, проходящей через два боковых ребра, не принадлежащие одной грани.
как найти диагонали правильного шестиугольника, если известна длина его стороны?\(CE\) — одна из коротких диагоналей шестиугольника, \(BE\) — одна из длинных диагоналей.
Учитывая то, что углы правильного шестиугольника равны \(120\) градусов, легко найти прямоугольный треугольник, в котором есть угол \(30\) градусов, и использовать соотношения в этом треугольнике.
Двугранный угол представляет собой фигуру, образованную двумя полуплоскостями и общей ограничивающей их прямой. Полуплоскости называются гранями двугранного угла, а прямая, ограничивающая их, - ребром (Рис.1).
Если провести плоскость, перпендикулярную ребру двугранного угла, то она пересечет его грани по двум полупрямым. Угол, образованный между двумя этими полупрямыми, называется линейным углом двугранного угла.
Градусная мера двугранного угла равна градусной мере линейного угла. Величина двугранного угла не зависит от выбора линейного угла, т.е. плоскости, перпендикулярной ребру двугранного угла.

Рис. 1 Двугранный угол.
Трехгранный углы
Пусть заданы три луча a, b, c не лежащие в одной плоскости и исходящие из одной общей точки О. (Рис.1.1). Тогда трехгранным углом называется фигура, которая состоит из трех плоских углов. Точка О, из которой исходят лучи, называется вершиной трехгранного угла. Сами углы называются гранями, а стороны - ребрами.
Понятие многогранного угла можно определить аналогичным образом.

Рис. 1.1 Трехгранный угол.
2.Призма и построение ее сечений
Прямая призма
Призмой называется многогранник, у которого две стороны являются плоскими многоугольниками, лежащими в параллельных плоскостях и совмещаемых параллельным переносом, а боковые грани состоят из всех отрезков, соединяющих соответствующие точки этих многоугольников (Рис.2). Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие точки оснований, ее ребрами.
Высотой призмы называется расстояние между ее основаниями.
Если боковые ребра призмы перпендикулярны основанию, то такая призма называется прямой. В противном случае призма называется наклонной. Боковые ребра у призмы параллельны и равны.
Боковые грани прямой призмы являются прямоугольниками. Если в основании призмы лежит правильный многоугольник, то такая призма называется правильной.
Теорема: площадь боковой поверхности прямой призмы равна произведению периметра основания призмы на ее высоту.
В основании призмы лежит правильный многоугольник. Боковые ребра призмы находятся под прямым углом к основанию и являются высотами. Боковые грани представляют собой прямоугольники. Отсюда следует, что площадь боковой поверхности призмы равна:
где
a1, a2, a3, . an - длины сторон основания
l - высота призмы
p - периметр основания
Полная площадь призмы равна сумме площадей двух оснований и боковой поверхности.

Рис.2 Прямая призма
Наклонная призма
Если боковые ребра призмы находятся под некоторым углом к основанию, то призма является наклонной (Рис.2.1).
Используя правила параллельного проектирования, изображение призмы можно построить следующим образом. Сначала строится одно из оснований, т.е. многоугольник, а затем проводят боковые ребра из каждой вершины основания, которые параллельны и равны между собой. Затем концы этих отрезков соединяются и строится другое основание призмы.
Для того, чтобы построить сечение призмы плоскостью, сначала задают прямую g в плоскости одного из оснований, которая называется следом. Затем проводят через заданную точку В прямую, которая находится в плоскости грани, и соединяют ее с заданным следом в точке Е. Отрезок АС на рассматриваемой грани есть пересечение этой грани с секущей плоскостью.
Если грань, которая содержит точку В, параллельна следу, то секущая плоскость пересекает эту грань по отрезку, параллельному заданному следу и проходящему через точку В.
Таким образом, можно провести отрезки на всех гранях призмы и получить сечение плоскостью с заданным следом.

Рис.2.1 Наклонная призма
3. Параллелепипед
Призма, у которой основание есть параллелограмм, называется параллелепипедом.
Параллелепипед, у которого грани расположены под некоторым углом ? 90° к основанию, называется наклонным. В противном случае - прямым, т.е. угол между боковыми гранями и основанием = 90°.
Теорема. Противолежащие грани параллелепипеда параллельны и равны.
Доказательство. Пусть дан параллелепипед ABCDA'B'C'D' (Рис.3). Рассмотрим грани параллелепипеда AA'D'D и BB'C'C. Так как основания параллелепипеда параллелограммы, то сторона AD параллельна и равна стороне ВС, а сторона A'D' параллельна и равна стороне B'C'. Сторона AB параллельна и равна стороне DС, а сторона A'B' параллельна и равна стороне D'C'. Отсюда можно сделать вывод, что грани AA'D'D и BB'C'C лежат в параллельных плоскостях. Таким образом, грань AA'D'D совмещается параллельным переносом с гранью BB'C'C. Следовательно эти грани равны.
Аналогично можно доказать параллельность и равенство граней DD'C'C и AA'B'B.
Центральная симметрия параллелепипеда
Теорема. Диагонали параллелепипеда пересекаются в одной точке, которая делит их пополам.
Рассмотрим две грани параллелепипеда ABCD и BB'C'C. Сторона BC у них общая. Следовательно стороны AD и B'C' равны, лежат на параллельных прямых и в одной плоскости. Так как грани параллелепипеда AA'B'B и DD'C'C лежат в параллельных плоскостях и совмещаются параллельным переносом, то диагонали AB' и DC' параллельны и лежат в плоскости сторон AD и B'C'. Отсюда можно сделать вывод, что AB'C'D - параллелограмм. Диагонали этого параллелограмма пересекаются в точке, которая делит их пополам.
Отсюда следует, что точка пересечения диагоналей параллелепипеда является его центром симметрии.

Рис. 3 Наклонный параллелепипед.
4.Прямоугольный параллелепипед
Прямой параллелепипед, у которого основание является прямоугольником, называется прямоугольным.
Длины не параллельных ребер параллелепипеда называются его линейными размерами.
Теорема. В прямоугольном параллелепипеде квадрат диагонали равен сумме квадратов трех его измерений.
Доказательство. Пусть дан параллелепипед ABCDA'B'C'D' (Рис.4). Рассмотрим прямоугольный треугольник ACC'. Cторонами данного треугольника являются диагональ параллелепипеда AC', диагональ основания AC и ребро боковой грани CC'. Тогда по теореме Пифагора находим:

Рис. 4 Прямоугольный параллелепипед.
AC' 2 = AC 2 + CC' 2
AC 2 = AD 2 + DC 2 Следовательно:
AC' 2 = AD 2 + DC 2 + CC' 2
Стороны AD, DC, CC' являются линейными размерами параллелепипеда.
Симметрия прямоугольного параллелепипеда
Прямоугольный параллелепипед имеет центр симметрии. Если все три измерения параллелепипеда разные, то он имеет три плоскости симметрии, которые проходят через центры граний (Рис.4.1)
Если параллелепипед имеет два равных измерения, то у него есть еще две плоскости симметрии, которые проходят через диагональные сечения.
Если у параллелепипеда все три линейные размера равны, то он является кубом. И у него девять плоскостей симметрии.

Рис. 4.1 Симметрия прямоугольного параллелепипеда.
5. Пирамида
Пирамидой называется многогранник, который состоит из многоугольника в основании, точки, не лежащей в плоскости основания, и всех отрезков, соединяющих вершины многоугольника и данную точку (Рис.5).
Точка, не лежащая в плоскости основания, называется вершиной пирамиды.
Отрезки, соединяющие вершины основания с вершиной пирамиды, называются боковыми ребрами.
Перпендикуляр, опущенный из вершины пирамиды на плоскость основания, называется высотой пирамиды.
На рисунке 5 изображена пирамида, в основании которой лежит правильный шестиугольник. A1A2A3A4A5A6
Построение пирамиды и ее плоских сечений
Для того чтобы построить пирамиду, необходимо сначала построить основание - плоский многоугольник. Затем взять точку, не лежащую в плоскости основания, и соединить ее боковыми ребрами с вершинами основания.
Сечения пирамиды, проходящие через ее вершину, представляют собой треугольники. Например, треугольниками являются диагональные сечения, т.е. сечения, проходящие через два несоседних боковых ребра .
Сечение пирамиды с боковым следом строится аналогично, как и сечение призмы (Рис.5). Т.е. сначала задается прямая в плоскости основания - след g. Затем берется какая-нибудь точка В, принадлежащая сечению, и строится пересечение следа g секущей плоскости c плоскостью этой грани - точка D. Полученный таким образом отрезок АС, представляет собой линию пересечения плоскости грани и плоскости сечения пирамиды.
Если точка В лежит на грани, параллельной следу g (Рис.5.1), то секущая плоскость пересекает эту грань по отрезку BC, параллельному следу g. Концы отрезка также соединяют со следом по прямой ED в плоскости a другой грани и получают прямую пересечения этой грани с плоскостью сечения и т.д. Таким образом можно построить линии пересечения плоскости сечения со всеми гранями пирамиды.


Рис. 5.1 Построение пирамиды и ее плоских сечений.
6. Усеченная пирамида
Теорема. Плоскость, пересекающая пирамиду и параллельная ее основанию, отсекает подобную пирамиду.
Пусть дана пирамида ABCDES. ABCDE - основание пирамиды, пятиугольник. S - вершина пирамиды. a - секущая плоскость. Подвергнем пирамиду преобразованию подобия (гомотетии) с коэффициентом подобия k относительно вершины S.

Так как при преобразовании подобия расстояние от вершины до точек фигуры изменяется в одно и тоже k число раз, то пятиугольник в основании переходит в плоскость a, параллельную основанию, т.е. секущую плоскость. Точки A'B'C'D'E' - точки пересечения боковых ребер пирамиды с плоскостью a. И пирамида, которая образуется путем отсечения данной пирамиды плоскостью a, является подобной данной.
Правильная пирамида
Если основание пирамиды есть правильный многоугольник, а основание высоты совпадает с центром этого многоугольника, то такая пирамида называется правильной.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Теорема. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.

Рис. 6 Усеченная пирамида.
7. Правильные многогранники
Если выпуклый многогранник имеет все грани правильные многоугольники с равным числом сторон и в каждой вершине многоугольника сходится одно и то же число ребер, то такой многогранник называется правильным.
Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
Тетраэдр это многогранник, у которого грани правильные треугольники.
Куб это многогранник, у которого все грани - квадраты.
Октаэдр - многогранник, который представляет собой две пирамиды с общим основанием. Основание этих пирамид - квадрат.
Додекаэдр это многогранник, у которого грани правильные пятиугольники. В каждой вершине сходится по три ребра.
Икосаэдр это многогранник, у которого грани правильные треугольники. В каждой вершине сходится по пять ребер.
Рис. 6 Правильные многогранники.
Репетитор: Васильев Алексей Александрович

2000 руб / 120 мин - подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин - индивидуально (базовый уровень). 2000 руб / 120 мин - студенты.
Предметы: математика, физика, информатика, экономика, программирование.
8. Пример 1
Докажите, что сечение призмы, параллельное основаниям, равно основаниям.
Доказательство:
Пусть дана призма АВСA'B'C' (Рис.7). Основания призмы равны и являются треугольниками. Они лежат в параллельных плоскостях и совмещаются параллельным переносом. Отсюда следует, что боковые ребра параллельны и равны.
Если провести плоскость a, параллельную основаниям, то в сечении получится такое же основание. Так как сторона A''C'' параллельна АС, A''B'' - AB, B''C'' - BC. А так как боковые ребра AA', BB', CC' параллельны, то АА"C''C, AA''B''B, BB''C''C прямоугольники (параллелограммы, если АВСA'B'C' наклонная призма).
Отсюда следует, что A''C'' = AC, A''B'' = AB, B''C'' = BC. Таким образом, треугольник A''B''C'' равен треугольнику АВС и A'B'C' соответственно. Отсюда можно сделать и общий вывод: если в основании призмы будет лежать како-либо многоугольник, то в сечении, параллельном основаниям, получится такой же многоугольник.

Рис.7 Задача. Докажите, что сечение призмы.
Пример 2
Боковое ребро наклонной призмы равно 16 м. Оно наклонено к плоскости основания под углом 30°. Найдите высоту призмы.
Решение:
Пусть дана наклонная призма АВСA'B'C' (Рис. 8). Рассмотрим нижнее основание - треугольник АВС. Проведем прямую а через точку А в плоскости основания, перпендикулярную A'A. Проведем также прямую АР, перпендикулярную прямой а. Таким образом, прямая АР является проекцией наклонной A'A на плоскость основания. А плоскость, в которой лежит треугольник AA'P, перпендикулярна плоскости основания.
Рассмотрим треугольник AA'P. Угол A'AP равен 30° по условию задачи. Опустим высоту A'O. В прямоугольном треугольнике AA'O найдем A'O.
sin 30° = A'O / AA' . Отсюда:
A'O = AA' sin 30° = 16 / 2 = 8 м.

Рис.8 Задача. Боковое ребро наклонной призмы равно 15 м.
Пример 3
В правильной четырехугольной призме через середины двух смежных сторон основания проведена плоскость, пересекающая три боковые ребра и наклоненная к плоскости основания под углом 60°. Сторона основания равна 8 м. Найдите площадь полученного сечения.
Решение:
Пусть дана правильна четырехугольная призма АВСDA'B'C'D' (Рис. 9). Заметим, что многоугольник PBCDF является проекцией многоугольника PKHSF на плоскость основания, площадь которого необходимо найти. Следовательно, найдем площадь многоугольника PBCDF.
SPBCDF = 8 2 - (8/2) 2 /2 = 56 м 2
Теперь найдем площадь многоугольника PKHSF из формулы:
SPKHSF = SPBCDF / cos 60° = 56 / 1 / 2 = 112 м 2

Рис.9 Задача. В правильной четырехугольной призме.
Пример 4
Боковая поверхность правильной четырехугольной призмы 12 м 2 . А полная поверхность 20 м 2 . Найдите высоту призмы.
Решение:
Пусть дана правильная четырехугольная призма АВСDA'B'C'D' (Рис. 10). Так как призма имеет четыре боковые грани, то площадь одной боковой грани составляет 1/4 часть боковой поверхности.
SAA'D'D = Sбок / 4 = 12 / 4 = 3 м 2
Площадь основания призмы равна половине разности площадей между полной поверхностью призмы и ее боковой поверхностью.
2 SABCD = Sпол - Sбок = 20 - 12 = 8 м 2
Так как площадь боковой грани составляет 3 м 2 , то высоту призмы, т.е. AA', можно найти из формулы:
Следовательно, высота призмы составляет 3 / 2 м.

Рис.10 Задача. Боковая поверхность правильной четырехугольной призмы.
Пример 5
Основание пирамиды - ромб с диагоналями 6 м и 8 м. Высота пирамиды проходит через точку пересечения диагоналей ромба и равна 7 м. Найдите боковую поверхность пирамиды.
Решение:
Пусть дана пирамида АВСDS (Рис. 11). Основание пирамиды - ромб ABCD с диагоналями АС = 8 м, BD = 6 м. Высота SO = 7 м.
По теореме Пифагора найдем боковые ребра SA и SD:
SA 2 = AO 2 + SO 2 = 4 2 + 7 2 = 65
SD 2 = OD 2 + SO 2 = 3 2 + 7 2 = 58
SA = , SD =
Теперь найдем сторону ромба AD:
AD 2 = AO 2 + OD 2 = 3 2 + 4 2 = 25 , AD = 5 м
Теперь по теореме косинусов найдем косинус угла a между боковыми ребрами:

AD 2 = SA 2 + SD 2 - 2 SA SD cos a = 65 + 58 - 2 cos a = 25

Читайте также:
