Как сделать пересечение плоскостей
В обоих случаях задача заключается в нахождении точек, общих для двух плоскостей.
Плоскости в пространстве могут занимать различное положение. рассмотрим три случая построения линии их пересечения.
- Линия пересечения двух проецирующих плоскостей
Если плоскости занимают частное положение, например, как на рис. 8, являются горизон- тально-проецирующими, то проекцией линии пересечения на плоскость проекций, которой данные плоскости перпендикулярны (в данном случае горизонтальной), будет точка. Фронтальная проекция линии пересечения перпендикулярна оси проекций.
В этом случае одна проекция линии пересечения совпадает с проекцией проецирующей плоскости на той плоскости проекций, которой она перпендикулярна.
На рис. 9 показано построение проекций линии пересечения горизонтально-проецирующей плоскости, заданной следами, c плоскостью общего положения (треугольник ABC).
На горизонтальной проекции (рис. 9) в пересечении следа плоскости PН и сторон АС и ВС треугольника АВС находим горизонтальные проекции n и m линии пересечения. По линиям связи находим фронтальные проекции точек M и N линии пересечения.
При взгляде по стрелке на плоскость V по горизонтальной проекции видно, что часть треугольника правее линии пересечения МN (mn) находится перед плоскостью Р, то есть будет видимой на фронтальной плоскости проекций. Остальная часть — за плоскостью Р, то есть невидима.
Линия пересечения двух плоскостей общего положения
Построение линии пересечения двух плоскостей общего положения осуществляется с помощью дополнительных плоскостей- посредников.
Общий прием построения линии пересечения таких плоскостей заключается в следующем. Вводим вспомогательную плоскость (посредник) и строим линии пересечения вспомогательной плоскости с двумя заданными. В пересечении построенных линий находим общую точку двух плоскостей. Чтобы найти вторую общую точку, повторяем построение с помощью еще одной вспомогательной плоскости.

Соединяем полученные точки М и N и определяем взаимную видимость фигур.
Задача. Построить линию пересечения двух плоских фигур, заданных треугольниками с координатами вершин:
На рис. 11 дано построение линии пересечения двух треугольников. Решение выполняем в следующей последовательности. Проводим две вспомогательные горизонтально-проецирующие плоскости — плоскость P через сторону ED и плоскость Q через сторону DF треугольника DEF. Плоскость P пересекает треугольник ABC по прямой 1-2.
В пересечении фронтальных проекций 1?-2? и d’e‘ находим фронтальную проекцию точки M(m’) линии пересечения. Плоскость Q пересекает треугольник ABC по прямой 3-4. В пересечении фронтальных проекций 3?-4? и b‘c‘ находим фронтальную проекцию точки N(п’) линии пересечения. Горизонтальные проекции этих точек, а следовательно, и линии пересечения, находим, проводя линии связи.
Соединяем точки M и N. Взаимную видимость треугольников на плоскостях проекций определяем с помощью конкурирующих точек.
С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку "Решить". Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Линия пересечения плоскостей - теория, примеры и решения
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости a1 и a2:
| a1: A1x+B1y+C1z+D1=0, | (1) |
| a2: A2x+B2y+C2z+D2=0, | (2) |
Найдем уравнение линии пересеченя плоскостей a1 и a2. Для этого рассмотрим следующие случаи:
1. Нормальные векторы n1 и n2 плоскостей a1 и a2 коллинеарны (Рис.1).
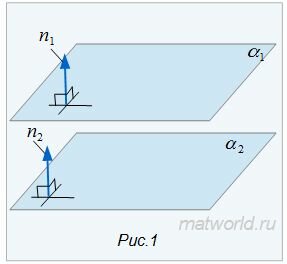 |
Поскольку векторы n1 и n2 коллинеарны, то существует такое число l?0, что выполнено равенство n1=ln2, т.е. A1=lA2, B1=lB2, C1=lC2.
Умножив уравнение (2) на l, получим:
| a2: A1x+B1y+C1z+lD2=0, | (3) |
Если выполненио равенство D1=lD2, то плоскости a1 и a2 совпадают, если же D1?lD2то плоскости a1 и a2 параллельны, то есть не пересекаются.
2. Нормальные векторы n1 и n2 плоскостей a1 и a2 не коллинеарны (Рис.2).
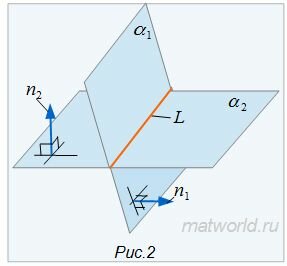 |
Если векторы n1 и n2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
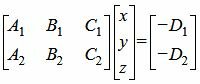 | (4) |
Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.
Так как в системе линейных уравнений (4) векторы n1=A1, B1, C1> и n2=A2, B2, C2> не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:
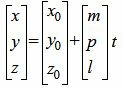 , | (5) |
где x0, y0, z0, m, p, l действительные числа, а t - переменная.
Равенство (5) можно записать в следующем виде:
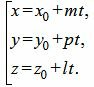 . | (6) |
Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей a1 и a2. Полученное уравнение прямой можно записать в каноническом виде:
Пример 1. Найти линию пересечения плоскостей a1 и a2:
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость a1 имеет нормальный вектор n1=A1, B1, C1>=. Плоскость a2 имеет нормальный вектор n2=A2, B2, C2>=.
Поскольку направляющие векторы n1 и n2 неколлинеарны, то плолскости a1 и a2 пересекаются.
Для нахождения линии пересечения влоскостей a1 и a2 нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:
 . | (9) |
Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 . | (10) |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 2 со строкой 1, умноженной на -2:
Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на -2/5:
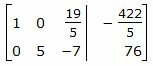 . |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 . |
 . | (11) |
где t- произвольное действительное число.
Запишем (11) в следующем виде:
 . | (12) |
Получили уравнение линии пересечения плоскостей a1 и a2 в параметрическом виде. Запишем ее в каноническом виде.
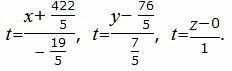 | (13) |
Из равентсв выше получим каноническое уравнение прямой:
 |
Ответ. Уравнение линии пересечения плоскостей a1 и a2имеет вид:
 |
Пример 2. Найти линию пересечения плоскостей a1 и a2:
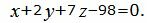 | (14) |
 | (15) |
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость a1 имеет нормальный вектор n1=A1, B1, C1>=. Плоскость a2 имеет нормальный вектор n2=A2, B2, C2>=.
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/2), то плоскости a1 и a2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости a2 умножив на число 1/2:
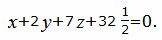 | (16) |
Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости a1 и a2 не совпадают. Следовательно они параллельны, т.е. не пересекаются.
Пример 3. Найти линию пересечения плоскостей a1 и a2:
 | (17) |
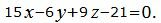 | (18) |
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость a1 имеет нормальный вектор n1=A1, B1, C1>=. Плоскость a2 имеет нормальный вектор n2=A2, B2, C2>=.
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/3), то плоскости a1 и a2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости a2 умножив на число 1/3:
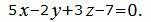 | (19) |
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости a1 и a2 совпадают.
Линия пересечения двух плоскостей представляет собой множество точек, которые общие для данных плоскостей. Из этих точек выделяют опорные, с которых и начинается построение линии. К ним относят верхнюю и нижнюю точки относительно той либо иной плоскости, точки, находящиеся в зоне видимости, и другие важные для построения этой линии точки.

- Как построить линию пересечения двух плоскостей
- Как определить видимость на чертеже
- Как построить сечение цилиндра
- - простой карандаш;
- - тетрадь;
- - ручка.
Внимательно изучите условия задания: от того, насколько правильно вы его поймете, во многом зависит окончательный результат.
Для построения линии пересечения двух плоскостей найдите две общие точки данных плоскостей, через которые в дальнейшем будете проводить прямую линию. Обратите внимание на то, что заданная треугольником ABC плоскость может быть представлена прямыми линиями (АВ), (АС), (ВС). Точку, с которой прямая (АВ) пересекается с плоскостью a', обозначьте D, а с прямой (AС) назовите точкой F. Таким образом, отрезок (DF) определит линию пересечения этих двух плоскостей. Ввиду того, что a является горизонтально проецирующей плоскостью, проекция отрезка D1F1 будет совпадать со следом от плоскости aП1. Отсюда выходит, что вам осталось лишь построить недостающие проекции отрезка (DF) на плоскостях П2, а также П3.
В том случае если даны плоскости общего положения, назовем их a(m,v) и b (ABC), построение линии между двумя плоскостями осуществите путем ввода двух вспомогательных секущих плоскостей (y и в). После этого найдите линии пересечения данных плоскостей с теми плоскостями, которые заданы по условию задания. Пусть плоскость y будет пересекаться с плоскостью a по прямой (12), а с плоскостью b - по прямой (34). Прямые (12) и (34) имеют общую точку пересечения Р, которая одновременно принадлежит трем плоскостям a, b и y. Предположите, что плоскость в пересекается с плоскостью a по прямой (56), а с плоскостью b - по прямой (78). Точка пересечения прямых (56) и (78) – К (она принадлежит трем плоскостям a, b и y, а также линиям пересечения плоскостей a и b). Ввиду этого, РК и будет линией пересечения плоскостей a и b.
В этом уроке рассмотрим одну из самых распространенных задач начертательной геометрии – построение пересечения поверхностей методом секущих плоскостей и способ ее решения средствами AutoСАD.

Метод секущих плоскостей, немного теории
Вкратце суть метода секущих плоскостей состоит в том, что для построения линии пересечения двух поверхностей строятся вспомогательные плоскости (обычно – параллельные одной из плоскостей проекций), которые пересекают заданные поверхности, образуя при этом простые геометрические фигуры.
Точки взаимного пересечения заданных поверхностей будут общими точками двух кривых, образованных пересечением секущей плоскости с каждой из поверхностей.
Условия задачи
Зададим условия: пусть необходимо построить пересечение полусферы и конуса, расположенных таким образом:

Размеры показаны для наглядности, проставлять их на чертеже не нужно.
Решение
Строим секущие плоскости, вид с боку
Очевидно, что для тел вращения удобно использовать плоскости, перпендикулярные осям этих тел. В нашем случае вспомогательные плоскости будут параллельными горизонтальной плоскости. Изобразим их на фронтальном виде (в нашем случае верхняя из плоскостей проходит через явно видимую верхнюю точку пересечения конуса и полусферы, в других случаях для нахождения этой точки потребуются дополнительные построения):

Секущие плоскости, вид сверху
Теперь перенесем линии пересечения секущих плоскостей с каждой из поверхностей на вид сверху. Очевидно, что горизонтальные плоскости пересекают каждое из тел по окружностям, центры которых находятся на одной вертикали с центрами тел. Радиусы этих окружностей легко переносятся на вид сверху с образующих каждой поверхности. Вот эти окружности для полусферы:


Точки пересечения секущих плоскостей
Отметим для наглядности общие точки для каждой из пар окружностей, образованных одной плоскостью:


Вот еще две точки, заданные этой плоскостью:

Линия пересечения
Соединив на виде сверху полученные точки сплайном (команда Сплайн), мы получим приближенную линию пересечения двух поверхностей:

Остается перенести линию на фронтальный вид. Сделать это совсем несложно: нужно перенести каждую из точек с вида сверху на соответствующую секущую плоскость на фронтальном виде. Линии построения выделены желтым цветом:


Проверка вида линии пересечения
Полезно проверить правильность наших построений средствами 3D-моделирования. Построим соответствующие фигуры, перейдя предварительно к интерфейсу 3D- моделирование , и сравним полученную модель с построением (для этого удобнее объединить объекты командой Объединить).


Резюме

Читайте также:
