Как сделать карты карно

Добавил пользователь Алексей Ф.
Обновлено: 30.08.2024

Пример карты Карно. Это изображение фактически показывает две карты Карно: для функции ? , используя минтермов (цветные прямоугольники) и для его дополнения, используя maxterms (серые прямоугольники). На изображении E () обозначает сумму minterms, обозначенную в статье как . ? м я >

Карта Карно снижает потребность в обширных вычислениях за счет использования возможностей распознавания образов людьми. [1] Это также позволяет быстро идентифицировать и устранять потенциальные условия гонки .

Требуемые булевы результаты передаются из таблицы истинности на двумерной сетке , где в карты Карно, клетки упорядочены в коде Грея , [6] [4] , и каждая позиция ячейка представляет одну комбинацию входных условий. Ячейки также известны как minterms, в то время как каждое значение ячейки представляет соответствующее выходное значение логической функции. Идентифицируются оптимальные группы единиц или нулей, которые представляют термины канонической формы логики в исходной таблице истинности. [7] Эти термины можно использовать для написания минимального логического выражения, представляющего требуемую логику.

Карты Карно используются для упрощения требований реальной логики, чтобы их можно было реализовать с использованием минимального количества логических вентилей. Выражение сумм из побочных продуктов (СОП) всегда может быть реализован с использованием логических элементов И запитывания в ИЛИ ворота и экспрессии продукта из-сумм (POS) приводит к ИЛИ ворота , питающие И вентиль. Выражение POS дает дополнение к функции (если F - функция, то ее дополнением будет F '). [8] Карты Карно также могут использоваться для упрощения логических выражений при разработке программного обеспечения. Логические условия, используемые, например, в условных операторах, может быть очень сложным, что затрудняет чтение и сопровождение кода. После минимизации канонические выражения суммы произведений и произведений сумм могут быть реализованы напрямую с помощью логических операторов И и ИЛИ. [9]

Диаграммные и механические методы минимизации простых логических выражений существуют по крайней мере со средневековых времен. Более систематические методы минимизации сложных выражений начали разрабатываться в начале 1950-х, но до середины-конца 1980-х карта Карно была наиболее часто используемым подходом. [10]

СОДЕРЖАНИЕ

• 1.1 Карта Карно
• 1.2 Решение
• 1.3 Обратный
• 1.4 Не волнует
• 2.1 Устранение
• 2.2 Примеры карт с двумя переменными

Карты Карно используются для упрощения функций булевой алгебры . Например, рассмотрим логическую функцию, описанную следующей таблицей истинности .

Таблица истинности функции

А	B	C	D	f ( A , B , C , D )
0	0	0	0	0	0
1	0	0	0	1	0
2	0	0	1	0	0
3	0	0	1	1	0
4	0	1	0	0	0
5	0	1	0	1	0
6	0	1	1	0	1
7	0	1	1	1	0
8	1	0	0	0	1
9	1	0	0	1	1
10	1	0	1	0	1
11	1	0	1	1	1
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	1
15	1	1	1	1	0

Ниже приведены два разных обозначения, описывающих одну и ту же функцию в неупрощенной булевой алгебре с использованием булевых переменных A , B , C , D и их обратных значений.

Созданную логическую схему можно сохранить в форматах docx и png (меню Действия ). По логической схеме можно построить СКНФ, СДНФ, полином Жегалкина, карты Вейча-Карно, а также минимизировать булеву функцию.

Инструкция к сервису

Для добавления логического элемента необходимо выделить его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле.
Чтобы соединить элементы, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить . Для соединения с переменной x_i нажмите на соответствующее ей название.

Булевы функции

С помощью этого калькулятора по булевой функции строится таблица истинности, определяются свойства функции и другие параметры (см. вкладку Параметры решения ). ? При этом вводится только само логическое выражение без префикса. Например, при f(x,y,z) = x -> y!z , ввести необходимо только x -> y!z .
Введеное выражение также можно упростить, используя законы логики высказываний (на следующем шаге выбрать параметр Упростить выражение ).

(. ) - ввод скобок, x -отрицание ( NOT , ! , ¬), & - логическое И, AND, ?, *, v - логическое ИЛИ, OR, ?, = - эквивалентность, ~, ?, <->, ? - сумма по модулю 2, | - штрих Шеффера, И-НЕ, AND-NOT, ? - стрелка Пирса, ИЛИ-НЕ, OR-NOT, <- - обратная импликация.

Для вложенного отрицания необходимо использовать знак ! . Например, x v y = !(x v y ) или x v y = x v !y
Далее Построить схему

По найденной таблице истинности можно определить логические значения высказываний, например, при x=0 , y=0 , z=1
Чтобы проверить высказывание на истинность или ложность, функцию необходимо вводить без знака равно ( = ). Например, A+B -> A&B =1 , необходимо ввести A+B -> A&B . Если в результате преобразований получится, что f=1 , то высказывание истинно, если f=0 - ложно.

Логические (функциональные) элементы являются наиболее распространенными: в силу полноты системы любую булеву функцию (БФ) можно представить в виде суперпозиции дизъюнкции, конъюнкции и отрицания. В качестве функциональных элементов (ФЭ) можно рассматривать любые булевы функции, при этом их можно соединять друг с другом, подавая выходы одних элементов на входы других (суперпозиция БФ).

Отрицание, ¬

Конъюнкция, &

Дизъюнкция, v

Сумма по модулю 2, x?y

Стрелка Пирса, x?y

Эквивалентность, x<->y

Импликация, x->y

Штрих Шеффера, x|y

Основные равносильности логики высказываний

Название	Формула
Закон исключенного третьего	X v !X ? И
Закон противоречия	X & !X ? Л
Закон коммутативности	X & Y ? Y & X X v Y ? Y v X
Закон ассоциативности	(X & Y)&Z ? X&(Y&Z) (X v Y) v Z ? X v (Y v Z)
Закон дистрибутивности	X&(Y v Z) ? X&Y v X&Z X v Y&Z ? (X v Y)&(X v Z)
Закон двойного отрицания	!!X ? X
Закон идемпотентности	X&X ? X, X v X ? X
Законы де Моргана	!(X v Y) ? !X & !Y !(X & Y) ? !X v !Y
Закон поглощения	X v X&Y ? X X&(X v Y) ? X
Законы склеивания	(X & Y)v(X & !Y) ? X (X v Y)&(X v !Y) ? X
Замена импликации	X -> Y ? !X v Y
Замена эквиваленции	X = Y ? X&Y v !X&!Y

Пример . Упростите выражение: (x?y?z)->(x?y)*(x?z)
Упростим функцию, используя основные законы логики высказываний.
Замена импликации: A -> B = !A v B
Для нашей функции:
(x v y v z)->((x v y) (x v z)) = x v y v z v (x v y) (x v z)
Упростим функцию, используя законы де Моргана: !(A v B) = !A & !B
Для нашей функции:
x v y v z = x y z
По закону дистрибутивности:
(x v y) (x v z) = x v x z v y x v y z
получаем:
f = x y z v x v x z v y x v y z
После элементарных преобразований получаем:
f = x y z v x v x z v y x v y z = x y z v x v y z
f = y z v y z v x

Минимизация булевых функций

В данном сервисе для минимизации булевых функций используются метод Квайна и карт Карно-Вейча. После получения минимальной формы имеется возможность заново построить логическую схему. Если исходная схема понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить ).

1. Kx v K ? K - тождество поглощения;
2. Kx v K x ? K - тождество склеивания;
3. Kx v Ky ? K(xvy) - дистрибутивный закон,

Метод карт Карно

После минимизации можно получить логическую схему функции и построить таблицу истинности (кнопка Далее )
Далее

Минимизая функции через равносильные преобразования

Алгоритм минимизии логической функции

1. Замена импликации и эквиваленции.
2. Упрощение функции через законы де Моргана.
3. Раскрытие скобок, используя законы поглощения, исключенного третьего, противоречия.
4. Минимизация через закон дистрибутивности.

Алгоритм Куайна построения сокращенной ДНФ

1. Получить СДНФ функции.
2. Провести все операции неполного склеивания.
3. Провести все операции поглощения.

Построение логической схемы по таблице истинности

По заданной СДНФ (по таблице истинности) создается новая логическая схема (если не выбран пункт Строить новую схему при минимизации булевой функции). Если вычисления происходят по исходной схеме и она понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить ).

Пример . Найдите СДНФ(А) и СКНФ(А) с помощью равносильных преобразований и таблицы истинности, если A = x v y v(x->y)&x

Карта Карно является специальной формой таблицы истинности, позво­ляющей не только задать логическую функцию, ко и выполнить и её минимизацию.

Рассмотрим логическую функцию, зависящую от 3-х логических переменных, заданную следующей таблицей истинности (таблица 1).




Карта Карно содержит 2 п клеток , расположенных в виде строки (п = 1, 2), либо в виде двумерной матрицы (п > 2). Каждая клетка, как и строка в таблице истинности, соответствует одному набору логических переменных. Для того, чтобы можно было производить минимизацию логической функции, необходимо в смежных в геометрическом смысле клетках карты расположить соседние наборы.

Это можно обеспечить, если наборы переменных, оп­ределяющих "координаты" клетки карты Карно, расположить в циклическом коде Грея, у которого каждое следующее значение отличается от предыдущего только в одном разряде.




На рис. 1 представлена так называемая эталонная карта Карнодля п = 3. Эталонная карта Карно служит для указания расположения переменных, как координат клеток, так и наборов этих переменных. Координатой клеток в горизонтальном направлении служат наборы переменных а координатой клеток в вертикальном направлении служит одна переменная х₂.




Рис. 1. Эталонная карта Карно для п = 3.

Каждая из п переменных встречается в половине наборов без ин­версии, а в другой половине с инверсией. Три толстые линии, расположенные с внешней стороны карты Карно, указывают, что в соответствующих им половинах клеток указанная рядом с этой линией переменная встречается в наборе без инверсии и, соответственно, в другой половине с инверсией. Правильность оформления эталонной карты Карно можно проверить следую­щим образом. Если толстую линию, соответствующую переменной х₂ протянуть вправо по горизонтали над клетками карты Карно, то она пройдет над клетками, в которых минимальный номер набора должен совпадать с весом переменной , рав­ным 2 2 = 4. Аналогично толстая линия, соответствующая переменной , при пере­мещении вниз по вертикали пройдет над клетками, в которых минимальный номер набора должен совпадать с весом переменной , равным 2 1 = 2. Это должно вы­полняться для всех переменных.

Несмотря на то, что карты Карно изображаются на плоскости, с точки зрения обеспечения соседства их клеток, карты нужно считать трехмерными объектами, так как клетки, расположенные на концах одних и тех же строк и столбцов, также явля­ются соседними. Так карту для трех переменных следует рассматривать как цилиндр со склеенными правым и левым краями. Карту Карно для четырех переменных нужно считать склеенной не только по правому и левому краям, но и по верхнему и нижнему. Таким образом, карта Карно для четырех переменных должна рассматриваться как поверхность тора.

Рабочая карта Карно, соответствующая табл.1, будет иметь вид, представлен­ный на рис. 2.







Рис. 2. Рабочая карта Карно для логической функции, заданной таблицей 1.

Буква урядом с косой линией, расположенной в левом верхнем углу карты Кар­но, обозначает реализуемую логическую функцию, а цифры 0 и 1 в клетках карты указывают значения этой функции на соответствующих наборах. Полученную рабочую карту Карно можно интерпретировать как компактное представление логической функции в СДНФ , либо в СКНФ. Дальнейшее изложение будем вести в предположении, что минимизация ведется в дизъюнктивных формах.

Процесс минимизации с помощью карт Карно базируется на использовании операции склеивания и основан на следующих положениях:

1.На картах Карно необходимо выделить монолитные области единичных клеток, образующих строку, столбец, прямоугольник или квадрат и содержащие одну, две, четыре, восемь и т. д. клеток. Эти выделенные области (или контуры покрытия) будут соответствовать импликантам. Очевидно, что одна изолированная клет­ка будет соответствовать конституенте единицы. Две смежные клетки будут соот­ветствовать импликанте, ранг которой r= п -1, четыре смежные клетки будут со­ответствовать импликанте, ранг которой г = п -2и т.д.

2.Переменные, от которых импликанта не зависит, входят в соответствующий выде­ленный контур как в виде , так и в виде , а остальные переменные только либо в виде , либо в виде

3.На основании закона тавтологии любая единичная клетка может быть включена в любое число различных контуров.

4.Для получения минимальных ДНФ в карте Карно не должно быть лишних по­крытий, то есть каждую единичную клетку достаточно использовать хотя бы один раз.

5. Существуют эквивалентные покрытия для получения различных минимальных ДНФ.

6.Существуют функции, для которых СДНФ совпадает с минимальной ДНФ. В этом случае на карте Карно все единичные клетки изолированные.

7.Если в карте Карно нет ни одной 1, то логическая функция эквивалентна константе 0. Если нет ни одного 0, то логическая функция эквивалентна константе 1. Если единицы занимают половину клеток карты Карно и представляют из себя монолитный массив в виде строки, столбца, прямоугольника или квадрата, то соответствующая импликанта состоит из одной переменной со знаком или без знака инверсии.

С учетом сказанного на картах Карно рис. 3 можно выделить три контура, со­держащих по две единицы.




Рис. 3. Рабочие карты Карно с двумя эквивалентными покрытиями

Два варианта покрытия обусловлены тем, что 1 в клетке с. набором 5 может образовать контур из двух клеток либо с набором 4 (рис. 3а), либо с набором 1 (рис. 3б).

Поясним получение импликанты для контура, образованного двумя клетками в нижней строке карты. Переменная входит в этот контур только с инверсией, переменная входит в этот контур и с инверсией и без инверсии, поэтому по ней осуществляется склеивание, и она исчезает, переменная входит в этот контур только без инверсии, поэтому импликанта имеет вид . Для выявленных двух покрытий можно запи­сать:




Простота получения этих уравнений показывает существенное преимуще­ство табличного метода карт Карно перед расчетным методом.

На рисунке 4 показаны эталонные карты Карно для п = 4, п =5 и п =6, причем карты Карно для п =5 и п =6 можно рассматривать как соответственно две и четыре карты Карно для п= 4, имеющие общие границы (они выделены толстыми центральными линия­ми). Карты Карно для п = 4, являющиеся составной частью карт Карно для п= 5 и п =6 и имеющие общие границы, называются соседними. Правило соседства, для какой либо клетки в этих случаях, будет выглядеть так: для любой выделенной клетки соседними являются четыре соседние клетки в карте Карно для п =4 и клетки, расположенные в соседних картах Карно для п =4 симметрично выделенной клетке относительно гра­ниц соседних карт Карно.

Пример. Для клетки с набором 25 на рис. 4,б соседними являются клетки с но­мерами наборов 9, 27, 17, 24 и 29. Для клетки с набором 2 на рис. 4,б соседними яв­ляются клетки 3, 10, 0, 18 и 6. Для клетки с набором 43 на рис. 4,в соседними являют­ся клетки с наборами 59, 42, 35, 41 и 47, 11. Для клетки с набором 22 на рис. 4,в со­седними являются клетки с наборами 23, 30, 20, 6 и 54, 18.







Рис. 4. Эталонные карты Карно для п =4, п =5 и п =6.




Рассмотрим еще несколько примеров для функций, зависящих от 4-х, 5-ти и 6-ти переменных. На рис. 5,а четыре 1-е клетки образуют квадрат, которому соответст­вует импликанта . На рис. 5,б контур, выделенный штриховой линией, ока­зывается лишним, так как все его клетки являются составными частями четырех кон­туров из двух клеток.

Из карты Карно (рис. 5,б) получаем:




.

Для карты Карно (рис. 5,в) покажем еще один способ определения импликант, соот­ветствующих выделенным контурам, состоящих в данном случае из двух столбцов. Для левого контура запишем минимальный и максимальный наборы . Таковыми являются наборы 2 и 14. Запишем их двоичные представления 0010 и 1110 одно на другом 1110. Переменные, соответствующие позициям с наложенными 0 и 1, склеиваются, а совпадающие позиции соответствуют искомой импликанте .Аналогичная процедура для правого контура дает импликанту . В итоге полу­чаем:










Рис.5. Рабочие карты Карно произвольных логических функций,зависящих от четырёх переменных




Если теперь на той же карте Карно выделить контуры, соответствующие импликантам (см. рис. 5,г), то окажется, что общая часть этих контуров бу­дет содержать нулевые клетки.




Преобразуем это выражение:

Для логической функции, представленной на рис. 5,д, можно записать:







Если на той же карте Карно выделить контуры, соответствующие импликантам (см. рис. 5,е), то окажется, что общая часть этих контуров содержит

нуль. Теперь можно сделать следующий вывод: если в карте Карно можно выделить два пересекающихся контура с общей нулевой частью, то импликанты, соответст­вующие этим контурам, объединяются знаком операции "сумма по mod2".

Картам Карно, показанным на рис. 6,а-г, соответствуют следующие выражения:

де-Мор-гана, то получим следующее выражение:







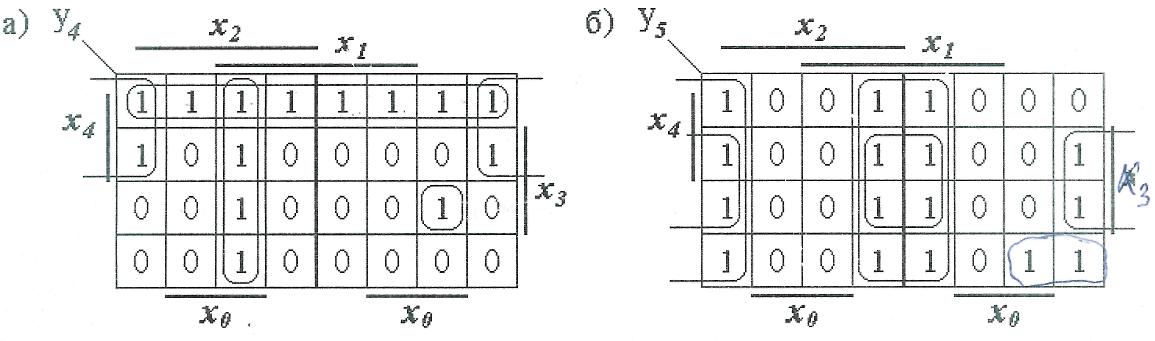
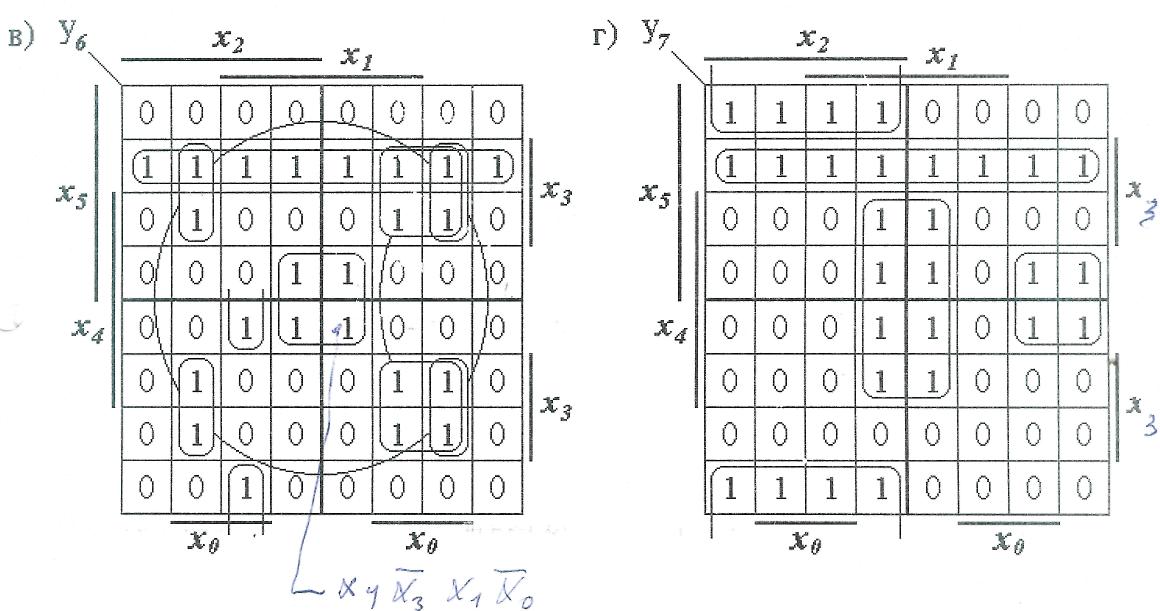
Рис 6. Рабочие карты Карно произвольных логических функций, зависящих от пяти и шести переменных













Карты Карно удобно использовать и для минимизации не полностью определен­ных функций. Безразличные значения логической функции на

картах Карно обозначаются каким-либо символом: крестиком, чертой, буквой и т. п. Карта Карно для этого случая приведена на рис. 7.




Рис.7. Рабочая карата Карно для не полностью определенной логической функции.

Доопределив безразличные значения у₈ на наборах 14 и 15 единицами, получим сле­дующее минимальное выражение:




После реализации этой функции она становится полностью определенной, то есть на безразличных наборах, включенных в контур, будут реализовываться значе­ния 1, а на не включенных в контур - значение 0.

Сформулируем в заключение достоинства и недостатки метода минимизации логических функций с помощью карт Карно.

Достоинства:

1.Основным достоинством применения карт Карно является компактность, простота и наглядность представления полностью и не полностью определенных логических функций.

2.Их применение оправдано для п = 2, п = 4, п = 5 и п =6, а при определенных навыках даже для п =7 и п =8, что соответствует большинству реально встречающихся задач.

3.Карты Карно можно использовать для минимизации ФАЛ, заданных как в СДНФ, так и в СКНФ.

4.Удобно минимизировать системы булевых функций, так как на картах Карно легко выделять общие части реализуемой системы логических функций.

5.Легко находятся минимальные комбинации контуров по их виду на карте Карно.

6.Карты Карно сразу позволяют реализовать первые два этапа минимизации (склеивание и выявление лишних импликант).

1.Затруднительно использовать карты Карно при п > 6.

2.Метод не является алгоритмическим, многое зависит от на­выков разработчика. Удобство обращения и экономия времени во многом зависит от его способности распознавать оптимальные конфигурации покрытия карт Карно.




Карта Карно? — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.

В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.

Содержание

Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:




Аналогично для КНФ:




Возможность поглощения следует из очевидных равенств




Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.

Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2 N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.

На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:

В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.

Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:

_1\overline _2\overline _3 \vee X_1\overline _2\overline _3 \vee \overline _1\overline _2X_3 \vee X_1\overline _2X_3 =" />
_2 (\overline _1\overline_3 \vee \overline _1X_3 \vee X_1\overline _3 \vee X_1X_3) = \overline _2 (\overline _1 \vee X_1)(\overline _3 \vee X_3) = \overline _2 " />


В общем случае можно сказать, что 2 K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.


Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.

Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 приведены на рисунке. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки. Для таблиц 5 и более переменных нужно учитывать также, что квадраты 4х4 виртуально находятся друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 являются сосоедними, и соответствующие им термы можно склеивать.

Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.

Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):




1. объединяем смежные клетки содержащие единицы в область, так чтобы одна область содержала 2 n ( n целое число = 0…) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;
2. область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);
3. не смежные области расположенные симметрично оси(ей) могут объединяться в одну;
4. область должна быть как можно больше, а кол-во областей как можно меньше;
5. области могут пересекаться;
6. возможно несколько вариантов накрытия.

Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например(для Карт на 2-ве переменные):

Для КНФ всё то же самое, только рассматриваем клетки с нулями, не меняющиеся переменные в пределах одной области объединяем в дизъюнкции (инверсии проставляем над единичными переменными), а дизъюнкции областей объединяем в конъюнкцию. На этом минимизация считается законченной. Так для Карты Карно на рис.1 выражение в формате ДНФ будет иметь вид: \ \overline\vee X1X2X4\vee \overline\ \overline" />

В формате КНФ:
)(X2\vee \overline)(\overline\vee \overline \vee X4)" />

Так же из ДНФ в КНФ и обратно можно перейти использовав Законы де Моргана.

У мальчика Коли есть мама, папа, дедушка и бабушка. Коля пойдёт гулять на улицу, если ему разрешат хотя бы двое родственников.
Для краткости обозначим родственников Коли через буквы:
мама — х1
папа — х2
дедушка — х3
бабушка — х4
Условимся обозначать согласие родственников единицей, не согласие нулём. Возможность пойти погулять обозначим буквой f, Коля идёт гулять — f = 1, Коля гулять не идёт — f = 0.
Составим таблицу истинности:





Перерисуем таблицу истинности в 2-х мерный вид:



Переставим в ней строки и столбцы в соответствии с кодом Грея. Получили Карту Карно:








Заполним её значениями из таблицы истинности:



Минимизируем в соответствии с правилами:





1. 1. Все области содержат 2^n клеток;
2. 2. Так как Карта Карно на четыре переменные оси располагаются на границах Карты и их не видно (подробнее смотри пример Карты на 5 переменных);
3. 3. Так как Карта Карно на четыре переменные все области симметрично осей — смежные между собой (подробнее смотри пример Карты на 5 переменных);
4. 4. Области S3, S4, S5, S6 максимально большие;
5. 5. Все области пересекаются (не обязательное условие);
6. 6. В данном случае рациональный вариант только один.


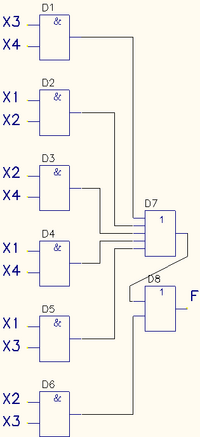
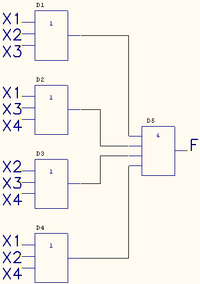
Теперь по полученной минимальной ДНФ можно построить логическую схему:





Из за отсутствия в наличии шести-входового элемента ИЛИ, реализующего функцию дизъюнкции, пришлось каскадировать пяти- и двух-входовые элементы(D7, D8).

Составим мин. КНФ:












Имеем такую таблицу истинности:





Карта Карно будет выглядеть следующим образом (для лучшего визуального восприятия в Карту нули не записываем):





Неправильно (на примере ДНФ):



• — Область S1 — накрыта правильно;
• — Область S2 — нарушает п.1;
• — Область S3 — нарушает п.2;
• -Области S4 и S6 — не выполняют п.3, это не является ошибкой — выражение получится больше чем если бы S4 и S6 представляли собой одну область;
• — Область S5 — нарушает п.1 по кол-ву клеток и по недопустимости нахождения нулей в области.




Правильно, но не оптимально:

Эта карта Карно минимизирована неоптимально, так как можно объединить единицы, входящие в члены S3 и S5.

Минимизировав эту Карту получаем следующую ДНФ:

\ \overlineX3X5\ \vee\ X1\overline\ \overline\ \overline\ \vee\ \overline\ \overlineX4\overline\ \vee\ \overline\ \overlineX4\overline\ \vee\ \overline\ \overline\ \overline\ \overline\ \vee\ X1X4X5" />










Составим минимальную КНФ:

\vee\overline\vee X5)(X3\vee X4\vee\overline)(\overline\vee\overline\vee X4)" />
\vee X4\vee\overline)(X1\vee X3\vee\overline\vee\overline)(X1\vee\overline\vee\overline) (X1\vee\overline\vee X4\vee X5)" />


Другой вариант той же самой Карты Карно:





Ничего не меняется только в строках записано три переменных, а в столбцах две.





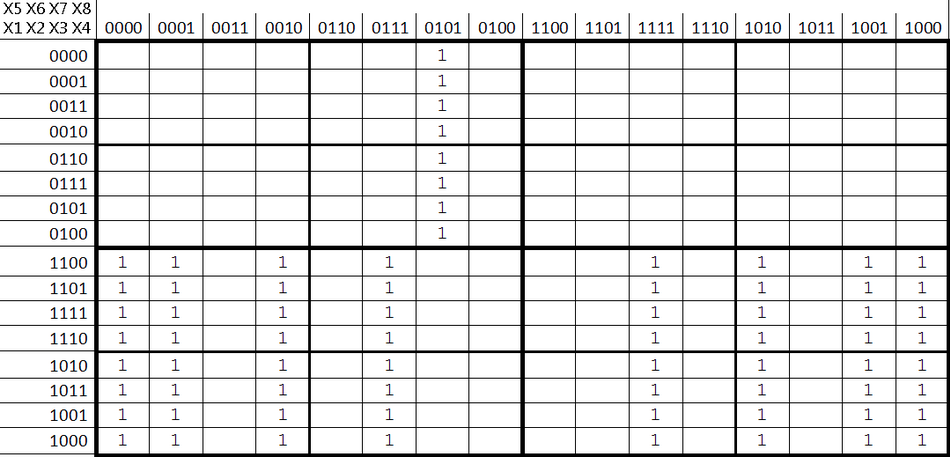
Предположим, по имеющейся таблице истинности составлена такая Карта Карно:

Найдём минимальную ДНФ: \ \overline\ \vee\ X1\overlineX7\overline\ \vee\ X1X6X7X8\ \vee\ \overline\ \overlineX6\overlineX8" />


Минимальная КНФ:
\vee\overline\vee X7) (X6\vee\overline\vee\overline)(\overline\vee X8)(X1\vee X6)(X1\vee \overline\vee\overline)(X1\vee \overline)" />


Карта Карно (минимизирующая карта) — это развертка некоторой объемной фигуры на плоскости. Карта Карно состоит из клеток, число которых равно числу наборов переменных функции. Каждая клетка соответствует строго определенному набору.

Например, карта Карно одной переменной (рис. 1.14): п = 1, число наборов N = 2" = 2.




Рис. 1.14. Карта Карно одной переменной

Карта Карно двух переменных (рис. 1.15): п = 2, число наборов N=2 2 - 4.




Рис. 1.1 5. Карта Карно двух переменных

Крайние клетки, соответствующие комбинациям 00 и 10, являются соседними и отличаются одной переменной а.

Переменные в карте могут располагаться произвольно, но любые соседние по вертикали ши по горизонтали клетки могут отличаться не более чем одной переменной.

Карта Карно трех переменных (рис. 1.16): п = 3, число наборов Л г = 2 3 = 8.




Рис. 1.16. Карта Карно трех переменных

Если имеется функция трех переменных, заданная таблицей истинности, представленной ниже, то соответствующая ей карта Карно выглядит так, как показано на рис. 1.17.




Рис. 1.17. Карта Карно функции

Обычно нули в карту не пишут, а заносят только единицы. Карта Карно четырех переменных (рис. 1.18): я = 4, JV = 16.




Рис. 1.18. Карта Карно функции четырех переменных

В этих картах переменные расположены но-разному, но они обе правильны, так как любые соседние клетки по горизонтали или вертикали отличаются только одной из переменных. Клетки верхнего ряда — соседние с клетками нижнего ряда, а клетки крайнего правого столбца — соседние с клетками крайнего левого столбца.

Карта Карно пяти переменных (рис. 1.19): п = 5, N=32. Это две 16-клеточные карты, отличающиеся только одной (пятой) переменной.




Рис. 1.19. Карта Карно функции пяти переменных

Карта Карно шести переменных (рис. 1.20): п = 6, N = 64. Это четыре 16-клеточные карты.




Рис. 1.20. Карта Карно функции шести переменных

Здесь любые клетки соседние, если они отличаются только одной переменной.

После заполнения карты единицами из таблицы истинности приступают к минимизации. Суть минимизации: охватить все единицы карты Карно наименьшим числом кубов наиболее высокого ранга. Из каждого куба выписывают минтерм общих переменных. Минтермы объединяют дизъюнктивно.

Куб — это прямоугольный или квадратный контур, содержащий клетки только с единицами:

Куб не может содержать другое число единиц и клетки с нулями. Одна и та же единица одновременно может принадлежать нескольким кубам, чтобы ранг куба был наибольшим. Тогда форма будет именно минимальной.

Требуется найти МДНФ такой функции: F (a, b, с) = v(l, 3, 6, 7). Составим ее таблицу истинности:



Читайте также:

  
• Как сделать так чтобы парень дал второй шанс
  
• Как сделать солнышко из смайликов
  
• Как сделать портретную матрешку
  
• Как сделать массажное масло в домашних условиях для возбуждения мужчин
  
• Как сделать собаку в paint net