Как выглядит шифр в реальной жизни
Основы криптографии включают шифры, специальную терминологию и отдельные компоненты криптосистемы. Сегодня эта наука тесно связана с информационной безопасностью.
Примечание Вы читаете улучшенную версию некогда выпущенной нами статьи.
Задачи, которые решает криптография:
Квантовая криптография
Это уже не совсем основы криптографии, а более продвинутый уровень.
На приведённой диаграмме квантовое распределение ключей (протокол BB84), являющееся безопасным способом связи, который реализует криптографический протокол с участием компонентов квантовой механики. Он позволяет двум сторонам создавать общий закрытый ключ, известный только им.
Стоит поиграть: обзор головоломки Keep Talking and Nobody ExplodesХинт для программистов: если зарегистрируетесь на соревнования Huawei Cup, то бесплатно получите доступ к онлайн-школе для участников. Можно прокачаться по разным навыкам и выиграть призы в самом соревновании.
Перейти к регистрации
Полиморфизм
Основы шифрования и криптографии включают в себя полиморфизм. Это более продвинутая практика в криптографии и часто используется в техниках компьютерного шифрования. Такая техника, которая самостоятельно модифицирует криптоалгоритм после каждого выполнения, и на каждой итерации получаются разные результаты. Если понадобится зашифровать одну и ту же информацию два раза, то алгоритм выдаст разные шифротексты.
Криптография и защищённая связь: история первых шифров
Криптография и шифрование тысячи лет используются людьми для защиты своих секретов. С некоторой долей условности эту историю можно начать с Древнего Египта.
Древний Египет
Самый древний текст с элементами криптографии найден в гробнице древнеегипетского вельможи Хнумхотепа II, наследного князя и номарха города Менат-Хуфу, жившего почти 4000 лет назад. Где-то около 1900 г до н.э. писарь Хнумхотепа описывал жизнь своего господина в его гробнице. Среди иероглифов он использовал несколько необычных символов, которые скрывают прямое значение текста. Такой метод шифрования фактически представляет собой шифр подстановки, когда элементы исходного текста заменяются другими элементами по определённым правилам.

Символы из гробницы Хнумхотепа II и их расшифровка
По мере развития египетской культуры замены иероглифов встречались всё чаще. Есть разные версии, почему египтяне использовали такую систему шифрования. По одной версии, они хотели охранить свои религиозные ритуалы от обычных людей. По другой версии, таким образом писцы придавали тексту некий формальный вид, как в наше время юристы используют специфические выражения для замены обычных слов. Как и сейчас, египетская криптография тоже могла быть способом писца впечатлить других людей — показать, что он может изъясняться на более высоком уровне, чем они.
Древняя Греция

Пример скиталы
Скитала является примером перестановочного шифра, в котором элементы исходного текста меняют местами, а не заменяют другими символами. По современным стандартам скиталу было бы очень просто взломать, но 2500 лет назад очень мало людей умели читать и писать. Скитала обеспечила спартанцам защищённую связь.
Древний Рим

Пример шифра подстановки
В отличие от примера на этой иллюстрации, Цезарь обычно просто сдвигал буквы на некое определённое число. Это число было шифровальным ключом для его алгоритма. Случайный порядок замены символов обеспечивает гораздо лучшую безопасность благодаря большему количеству возможных таблиц замены.
Шифр Альберти-Виженера
В середине 15 века итальянский учёный, архитектор, скульптор, художник и математик Леон Батиста Альберти изобрёл систему шифрования на основе шифровального диска. Это было механическое устройство со скользящими дисками, которые допускали много разных методов подстановки символов. Это базовая концепция многоалфавитного шифра, в котором метод шифрования меняется непосредственно в процессе шифрования. В своей книге «Взломщики кодов» Дэвид Кан называет Альберти «отцом западной криптографии». Альберти никогда не реализовал свою концепцию шифровального диска, она осталась только на бумаге.

Шифровальный диск
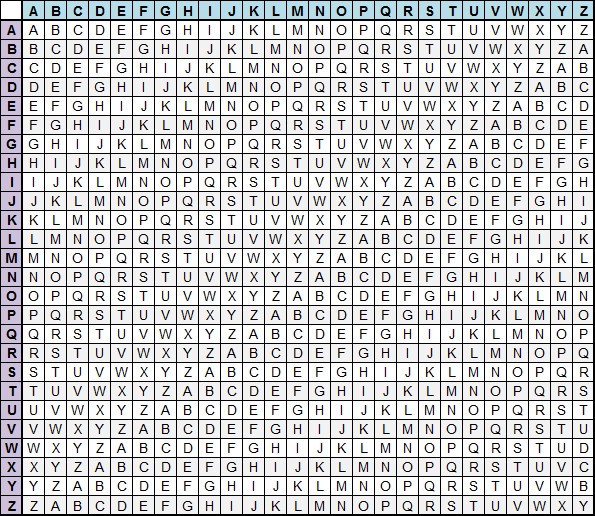
В 16 веке французский дипломат Блез Виженер на основе концепции многоалфавитного шифра Альберти создал шифр, который получил название шифра Виженера. Он работает точно как система Цезаря за исключением того, что ключ меняется в процессе шифрования. В шифре Виженера применяется решётка из букв, которая задаёт метод подстановки. Её называют квадратом Виженера или таблицей Виженера. Решётка состоит из 26 строк алфавита со смещением на один символ друг относительно друга.

Метод смены одного ключа на другой следует простому шаблону. В качестве ключа шифрования выбирается специальное секретное слово. Каждый символ в исходном тексте заменяется с использованием таблицы. Чтобы определить, на какую букву нужно заменить первый символ, мы совмещаем первый символ исходного текста (по одной оси) с первым символом секретного слова (по другой оси). Метод повторяется для второй и каждой последующей букв, секретное слово используется многократно, пока не закончатся символы в исходном тексте.
Предположим, что нужно зашифровать такую фразу:
Отправитель послания выбирает секретное слово и повторяет его до окончания исходного текста. Например, LEMON.
Для зашифровки первого символа нужно совместить строку A со столбцом L (в результате получается L), для шифрования второго символа — строку T со столбцом E (в результате получается X) и так далее. Вот как выглядит результат:
Расшифровка выполняется таким же способом: буква в тексте послания (диагональные строки таблицы) совмещается с буквой секретного слова в столбцах или строках таблицы.
Дисковый шифр Джефферсона
В конце 18 века Томас Джефферсон придумал шифровальную систему, очень похожую на шифр Виженера, но с лучшей защитой. Его шифратор состоял из 26 дисков с буквами алфавита, случайно размещёнными на каждом. Диски были пронумерованы и установлены на цилиндр в определённом порядке. Ключом является порядок дисков на оси.

Дисковый шифр Джефферсона
Как и Альберти, Джефферсон никогда не использовал свою систему шифрования. В начале 20 века шифровальщики американской армии придумали заново цилиндр Джефферсона, ничего не зная об этом изобретении. Джефферсон опередил своё время более чем на сто лет. Армия США использовала такую систему шифрования с 1923 по 1942 годы.
Распространённые алгоритмы
Сегодня шифры используют алгоритмы либо с секретным, либо с публичным ключом. В шифрах с закрытым ключом используется единственный ключ, которым обмениваются стороны. Такой ключ или шифр также называют симметричным.

В 1949 году Клод Шеннон из Bell Laboratories опубликовал фундаментальную теорию, положившую начало симметричному шифрованию, а десятилетия эволюции принесли примеры высокого качества. Однако только в 1975 году мощный алгоритм с закрытым ключом DES стал доступен для общего пользования.
Шифрование с помощью открытого ключа или асимметричное шифрование также возникло в середине 1970-х. Асимметричные шифры используют пару ключей — открытый, им делятся с другими людьми, и соответствующий ему закрытый, пользователь должен хранить его в секрете от других.
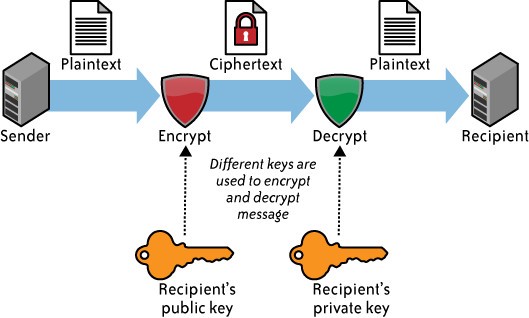
Стойкость шифровального алгоритма зависит от трёх важных факторов:
- Инфраструктура — если криптография встроена в ПО, то самым слабым звеном будет среда выполнения этого ПО.
- Длина ключа — практичный шифр должен использовать такую длину ключа, при которой полный перебор будет нецелесообразным.
- Качество алгоритма — ошибки шифрования могут ускорить процесс взлома для злоумышленников.
Элементарные шифры на понятном языке
Все мы довольно часто слышим такие слова и словосочетания, как «шифрование данных», «секретные шифры», «криптозащита», «шифрование», но далеко не все понимают, о чем конкретно идет речь. В этом посте разберемся, что из себя представляет шифрование и рассмотрим элементарные шифры с тем расчетом, чтобы даже далекие от IT люди поняли суть этого явления.
Прежде всего, разберемся в терминологии.
Ключ — это компонент, на основе которого можно произвести шифрование или дешифрование.
Шифр Атбаша
Например, есть у нас алфавит, который полностью соответствует обычной латинице.
Для реализации шифра Атбаша просто инвертируем его. «А» станет «Z», «B» превратится в «Y» и наоборот. На выходе получим такую картину:

И теперь пишем нужное сообшение на исходном алфавите и алфавите шифра
Шифр Цезаря
Опять же, для наглядности, возьмем латиницу
И теперь сместим вправо или влево каждую букву на ключевое число значений.
Например, ключ у нас будет 4 и смещение вправо.
Исходный алфавит: a b c d e f g h i j k l m n o p q r s t u v w x y z
Зашифрованный: w x y z a b c d e f g h i j k l m n o p q r s t u v
Шифруем его и получаем следующий несвязный текст:
Шифр Вернама (XOR-шифр)
Исходный алфавит — все та же латиница.

Теперь вспомним курс электроники и элемент «Исключающее ИЛИ», также известный как XOR.
XOR принимает сигналы (0 или 1 каждый), проводит над ними логическую операцию и выдает один сигнал, исходя из входных значений.
Если все сигналы равны между собой (0-0 или 1-1 или 0-0-0 и т.д.), то на выходе получаем 0.
Если сигналы не равны (0-1 или 1-0 или 1-0-0 и т.д.), то на выходе получаем 1.
Переведем их в бинарный код и выполним XOR:
В данном конкретном примере на месте результирующих символов мы увидим только пустое место, ведь все символы попали в первые 32 служебных символа. Однако, если перевести полученный результат в числа, то получим следующую картину:
С виду — совершенно несвязный набор чисел, но мы-то знаем.
Шифр кодового слова
Например, возьмем для разнообразия, кириллический алфавит.
Придумаем кодовое слово. Например, «Лукоморье». Выдернем из него все повторяющиеся символы. На выходе получаем слово «Лукомрье».
Теперь вписываем данное слово в начале алфавита, а остальные символы оставляем без изменений.
Получим в итоге следующий нечитаемый бред:
Шифр Плейфера
Пусть кодовое слово у нас будет «HELLO».
Сначала поступаем как с предыдущим шифром, т.е. уберем повторы и запишем слово в начале алфавита.
Разобьем его на биграммы, т.е. на пары символов, не учитывая пробелы.
Шифрование выполняется по нескольким несложным правилам:
1) Если символы биграммы находятся в матрице на одной строке — смещаем их вправо на одну позицию. Если символ был крайним в ряду — он становится первым.
Например, EH становится LE.

2) Если символы биграммы находятся в одном столбце, то они смещаются на одну позицию вниз. Если символ находился в самом низу столбца, то он принимает значение самого верхнего.
Например, если бы у нас была биграмма LX, то она стала бы DL.
3) Если символы не находятся ни на одной строке, ни на одном столбце, то строим прямоугольник, где наши символы — края диагонали. И меняем углы местами.
Например, биграмма RA.


Поздравляю. После прочтения этой статьи вы хотя бы примерно понимаете, что такое шифрование и знаете как использовать некоторые примитивные шифры и можете приступать к изучению несколько более сложных образцов шифров, о которых мы поговорим позднее.
Популярные шифры
Чтобы понять основы шифрования, необходимо обратиться к популярным примерам.
Квадрат Полибия
Квадрат Полибия — шифр простой замены. В данном примере будет использоваться двумерная матрица 6х6, содержащая заглавные буквы алфавита и цифры от 0 до 9:
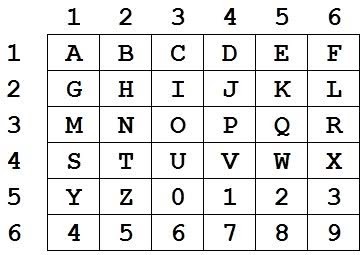
С матрицей 6х6 (36 буквенно-цифровых знаков) мы можем начать замену. Например, буква «А» имеет адрес 1х1 или x=1, y=1. Эту запись можно упростить до 11. Другой пример: адрес буквы «N» будет 2х3 или x=2, y=3 или 23.
Шифр может сделать достаточно длинным и сложным, используя прописные буквы и специальные символы. Также повторение символов и написание алфавита вразброс может дать непредсказуемый результат, устойчивый для метода полного перебора.
Шифр Цезаря

Пример использования шифра со сдвигом влево на 3:
Прим. пер. Существует более простой способ взлома шифра Цезаря — частотный анализ. Он заключается в подсчёте частоты встреч каждого символа в любом обычном тексте и в шифротексте. Потом символы с похожими частотами заменяются. Например, если в шифротексте чаще всего встречается буква «T», то она заменяется на букву «Е» для английского алфавита. Этот способ действует только для текстов свыше 300 символов.
Квадрат Виженера
Также у нас есть статья, из которой вы узнаете о самых популярных кодах и шифрах.
Математический гений в криптографии: от сцитала до RSA

Под катом несколько исторических примеров систем шифрования, а также математические принципы, заложенные в современных алгоритмах с открытым и закрытым ключом. А поскольку все гениальное просто, в статье не будет сложных формул и чрезмерного занудства.
Этот пост — адаптация лекции Евгения Бережного, доктора физико-математических наук и профессора математического факультета ярославского Демидовского университета, которая прошла в Точке кипения ЯрГУ.
Давайте на примерах рассмотрим общие принципы криптографии, существовавшие до эпохи вычислительных машин.
Шифрование в древности: несколько примеров
Натан Ротшильд когда-то сказал легендарную фразу, что тот, кто владеет информацией — владеет миром.
И хотя с тех пор никто нам внятно так и не объяснил, зачем нужно этим миром владеть, информация в цене только растет.
Первые попытки закрыть информацию были, по теперешним меркам, наивно-примитивны: часть информации просто писали на другом языке.
Например, вместо греческого языка текст писали на латинском. Это делали для той части греков, которые не знали латынь.
Пример текста диалога Платона и Евтифрона на греческом и латинском языках под редакцией Роберта Этьена (репринт 1578 года)
Современная криптография работает по похожему принципу — изобретается некий «язык», который недоступен основной массе.
Сцитала — первый механический шифр
Одна из первых криптографических систем и первых попыток изобрести свой секретный язык — шифросистема сцитала (другое название — скитала).
Главная деталь такой системы — стержень или конус определенного диаметра. На него наматывали длинную полоску бумаги, на витках которой записывали текст. Затем бумагу снимали и отправляли, скажем, в другой город, где получатель имел цилиндр или конус аналогичной формы. Намотав такую бумагу на такой стержень, человек мог прочитать послание.
Чтобы такая система работала, необходимо, чтобы и на передаче, и на приёме для восстановления информации использовали один и тот же цилиндр. Это был один из самых первых известных нам механических шифров. И, если говорить современным языком, он был не очень криптостойким.
Шифр Цезаря
Подмену символов делали разными способами. Например, одному символу могли соответствовать сразу несколько символов алфавита. Для упрощения дешифровки использовали сдвиг алфавита на заданное число символов. Все эти типы шифров — вариации шифра Цезаря. В каждом таком случае для шифрования информации на передаче и дешифровки на приеме использовали один и тот же ключ — табличку с сопоставленными исходными и подменяемыми символами.
Поворотная решетка: надежный механический шифр
В результате написанный текст образовывал некий массив бессвязных символов. Для восстановления информации, то есть на приеме, использовали аналогичную поворотную решетку с тем же набором отверстий. Криптостойкость такой системы зависила от числа ячеек в решетке. Чем больше окошечек, тем выше стойкость шифрования поворотной решеткой.
Обычно под криптостойкостью понимают количество идентичных шифров, похожих на данный. Если вернуться к шифру Цезаря и нашему примеру с цифрами от единицы до пяти, то всего количество перестановок будет 5!. Поэтому криптостойкость нашего примера шифрования будет 1/5!. Это, конечно, не очень большое число, но если у нас 32 элемента в алфавите, то вероятность того, что мы угадаем шифр, уже будет 1/32!.
Если число элементов поворотной решетки вдоль одной стороны будет 4n, то криптостойкость метода составит 4 2n .
По мере развития криптографии появлялось все больше и больше «секретов», в то время как главный принцип — замещения — оставался неизменным.
Криптографические приемы нашли место во многих литературных произведениях, особенно в детективах. В рассказе «Пляшущие человечки» Конан Дойл описал шифр, где использовали принцип замещения — каждой букве присваивали свой рисунок человечка. Шерлок Холмс блестяще справился с разгадкой этого шифра, используя простую логику и принципы построения фраз.
Оригинальный шифр из книги Артура Конан Дойла. Человечки с флагами работают пробелами
Переход в эпоху вычислительной техники и создание несимметричного шифра
Промышленные криптосистемы появились позже, когда возникла необходимость скрывать большие объемы данных и ограничивать доступ к информации государственной важности. Во вторую мировую войну наибольшую известность обрела немецкая шифровальная машина «Энигма», историю которой все знают по фильмам «U-571», «Игра в имитацию» и других. В легендарной немецкой шифровальной машине тоже использовали шифр, основанный на шифре Цезаря, многократно усложненный.
Подробнее об алгоритме работе «Энигмы» можно узнать из этого ролика (eng.)
К середине восьмидесятых годов прошлого века никаких новых методов закрытия информации не появилось, и многие сочли криптографию устаревшей наукой.
Даже в опубликованной в 1988 году советской брошюре по криптографии было написано, что эта тема себя исчерпала и не может содержать ничего нового.
Автор брошюры ошибался. В это же время в Массачусетском технологическом институте трое сотрудников — Рональд Ривест, Ади Шамир и Леонард Адлеман — придумали новую шифросистему с высокой криптостойкостью, которая базировалась на принципах, отличных от тех, что использовались ранее.
Ади Шамир, Рональд Ривест и Леонард Адлеман — создатели алгоритма несимметричного шифрования
Для взлома этой системы на то время понадобилось бы примерно 10 тысяч лет.
До ее изобретения все шифровальные методы основывались на целочисленной арифметике и использовали все множество целых чисел. Уникальность нового метода в том, что он использовал также и арифметику остатков.
Предположим, у нас есть произвольное целое число n. И давайте возьмем m=5. Произвольное число n можно поделить на пять, в результате чего получится частное плюс остаток. Остаток может принимать значение 0, 1, 2, 3, 4. Оказывается, эти остатки могут вести себя как обычные числа. Запишем две таблицы — таблицу сложения для остатков и таблицу умножения для остатков.
Таблицы остатков от сложения и деления (плюс в карму тому, кто первый найдет у лектора ошибку, сделанную по невнимательности)
Имея на руках такие таблицы, можно опять получить новую арифметику. Объекты с такой новой арифметикой обозначаются как Z(m). Остаток от деления числа a на m записывается следующим образом: a mod m = b. Мы записали таблицы для числа пять — Z(5). Аналогичным образом можно записать такие таблицы для любого натурального числа Z(m).
Пример
Изобретатели нового шифра зашифровали фразу, где в качестве a было взято число 1007, m0 и m1 содержали примерно по 65 знаков в десятичной системе. Математики озвучили публичные а, зашифрованную фразу и m, предлагая всем желающим расшифровать секретную фразу. Также был опубликован алгоритм, как взломать эту систему. Вся криптостойкость определялась разложением m = m0 x m1.
История длилась 17 лет, пока с появлением интернета у пользователей не появилась возможность задействовать сеть компьютеров с распределенными вычислениями. За 220 дней около 1600 компьютеров смогли восстановить исходную информацию, разложив m на два простых числа. Это событие показало, что криптография как наука жива.
Также это доказало непостижимую эффективность математики при решении реальных задач. Сама же система получила название RSA — по именам своих создателей.
Практическое применение криптографии
С появлением интернета возник целый класс задач, для решения которых снова и снова приходится прибегать к математике. В частности, речь идет об удаленных и защищенных действиях. Используя интернет и инструменты для закрытия информации можно, скажем, открыть счет в банке, провести платеж без личного присутствия человека. Требования к таким криптосистемам отличаются от классических, присутствовавших в жизни человека раньше.
Если при зарождении криптографии на передаче и на приеме была одна и та же шифросистема — поворотная решетка, сцитала и т. д., — то теперь ситуация кардинально иная. На передаче и приеме в новых криптосистемах применяют совершенно разные методы обработки информации.
На передаче используют простые алгоритмы, чтобы закрыть информацию (в нашем случае — возвести x в степень a), а на приеме происходит быстрое восстановление (если вам заранее известно разложение m на m0 и m1). Получается несимметричная система шифрования, которая удобна и надежна.
По сравнению с симметричными системами шифрования, предложенный вариант не годится для передачи данных сверхбольшого объема ввиду ресурсоемкости операций. Зато в случае несимметричного шифра отпадает необходимость в передаче секретного ключа, что весьма удобно, если необходимо использовать сеансовый пароль.
Новые принципы криптографии привели к созданию цифровой подписи — механизму, который подтверждает аутентификацию пользователя.
Им можно подписывать документы и заверять свою личность — например, в финансовых документах.
Наш ГОСТ и американский стандарт цифровой подписи основаны на эллиптических кривых и решении логарифмических уравнений. Математика, которую там используют, очень сложна, и сегодня мы опустим эти математические выкладки.
Иногда криптографию применяют в неожиданных сферах, где требуется подтверждение достоверности информации. Например, если вы, расслабившись в конце рабочего дня, сядете играть в карты, то вы можете быть уверены в честной игре, даже не имея на руках реальных карт. Скрытую информацию с помощью описанных алгоритмов всегда можно восстановить и проверить. Тем же способом же можно организовывать честное голосование без необходимости физического присутствия человека на избирательном участке.
Математика позволяет решать самые разные и сложные задачи обеспечения информационной безопасности. И по мере развития вычислительных систем алгоритмы будут только усложняться.
Виды алгоритмов
DES выдержал испытание временем и вошёл в основы криптографии. После четверти века исследований учёным удалось найти несколько спекулятивных атак, которые в конечном итоге не были столь эффективными, как метод полного перебора. Единственная реальная слабость DES-шифра — маленькая длина ключа в 56 бит.
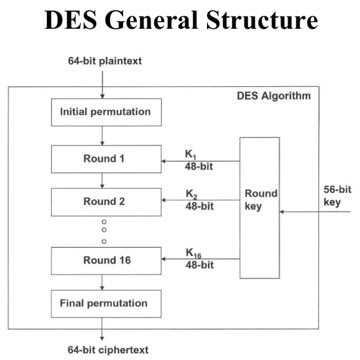
Triple DES (3DES) — модификация DES, позволяющая увеличить длину ключа до 112 или 168 бит.
Алгоритм шифрования Rijndael (AES)
Так как DES был специально разработан для аппаратного обеспечения, то не было предусмотрено, чтобы он эффективно работал в ПО. NIST протестировал работу алгоритма AES в программной среде и разработал требования к хранению криптоматериала, чтобы гарантировать, что AES будет эффективно работать на C и Java, которые используются на рабочих станциях, а также в более ограниченных средах встроенных процессоров ARM и смарт-карт.
Архитектура AES основана на принципе, известном как замена и перестановка, и быстро работает как в программном, так и на аппаратном уровнях. В отличие от своего предшественника — DES, AES не использует сеть Фейстеля.
Длина ключа, используемого для шифрования AES, указывает на количество повторений раундов преобразования, которые преобразуют входной сигнал, называемый исходным текстом, а конечный вывод — шифротекстом. Число циклов повторения выглядит следующим образом:
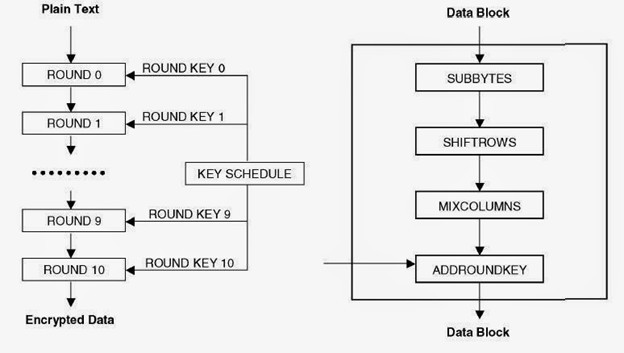
Каждый раунд состоит из нескольких этапов обработки. Набор обратных повторений применяется для преобразования шифротекста в исходный текст с использованием того же самого ключа шифрования.

Читайте также:
