Как сделать трисектор

Добавил пользователь Владимир З.
Обновлено: 10.09.2024

Презентация на тему: " Т РИСЕКТРИСА УГЛА. В 7 классе мы научились делить угол по полам, проводя биссектрису угла. Мы строили её с помощью линейки и циркуля. Построив угол, мы." — Транскрипт:

1 Т РИСЕКТРИСА УГЛА

2 В 7 классе мы научились делить угол по полам, проводя биссектрису угла. Мы строили её с помощью линейки и циркуля. Построив угол, мы проводили 2 полуокружности и соединяли отрезком угол и точку пересечения этих полуокружностей

3 Вскоре мы будем проходить трисектрису углов. Она делит угол уже не на 2 равные части, а на 3. Трисектрису нельзя построить только с помощью циркуля и линейки. Это было доказано Р. Декартом. Строгое доказательство о трисектрисе угла впервые было дано в 1837 году П. Ванцелем.

4 Для построения трисекции угла нам понадобятся: циркуль, линейка, не имеющая делений, небольшой полукруг и 2 полоски разной длины. Одна из них должна быть равна радиусу полукруга, другая произвольная. Построим простейший трисектор, как изображен на рисунке. Край произвольной полоски составляет прямой угол c углом окружности.

5 Разделим на 3 части угол KSM. Трисектор помещают так, чтобы вершина угла S находилась на линии BD,одна сторона угла прошла через точку A,а другая сторона коснулась полукруга. Затем проводят прямые SB и OS. Они и разделяют угол на 3 равные части. D S N A M K С

6 Доказательство: Соединим центр полукруга О с точкой касания N, ASB= BSO= OSN, отсюда следует и равенство углов: ASB= BSO= OSN

7 Открытия в геометрии треугольника есть и в 20 веке. Одно из интереснейших открытий было то, что если в треугольнике из всех углов провести трисектрисы, то при их пересечении получится равносторонний треугольник.

8 З АКЛЮЧЕНИЕ Трисектрису углов мы будем проходить в 9 классе, но у нас уже есть представление о том, что это такое и как их построить.

Давний автор журнала академик Николай Антонович Доллежаль - крупный специалист в области энергетики. В свободное время Николай Антонович занимается исследованием знаменитых задач древности, известных как трисекция угла, удвоение куба и квадратура круга (см. "Наука и жизнь" № 7, 1993 г.; №№ 3, 8, 1994 г.; № 9, 1995 г.). Сложность всех этих задач состоит в том, что решаться они должны без вычислений и расчетов, чисто геометрически, только с помощью циркуля и линейки без делений. Используя именно этот классический метод, Н. А. Доллежаль сумел найти очень изящное решение задачи о делении на три равные части произвольного угла.

Суть этой геометрической задачи заключается в отыскании графического метода деления произвольного угла на три равные части с помощью циркуля и обыкновенной линейки. Ниже приводим описание метода, решающего эту задачу независимо от размера и типа (острый, тупой) угла, предлагаемого для разделения. Ограничений на формы геометрических фигур нет, численных измерений или вычислений не делается. Для примера взят случайный угол.

Геометрические элементы комбинируются геометрической фигурой, состоящей из равнобедренного треугольника АВС с нижним углом В, подлежащим разделению на три равных угла, и равносторонней трапеции АDFC, все четыре угла которой находятся на равном расстоянии от вершины угла В. Треугольник и трапеция сомкнуты своими основаниями АС. Предлагаемый метод решения задачи состоит в следующем:

1) Основанием для построения упомянутой геометрической фигуры служат уравнения, связывающие основные ее элементы:

где S - основание треугольника и трапеции; а - сторона трапеции; t - высота треугольника; h - высота трапеции.

Главные элементы фигуры находятся во взаимной зависимости: отношения основания к стороне трапеции и высот трапеции треугольника связаны уравнением (2).

У отношений S/а и h/t есть пределы применимости: отношение основания трапеции к ее стороне находится в пределах 2 . 3, а отношения высот трапеции и треугольника изменяются при этом от бесконечности до 0. За пределами этих ограничений построение фигуры треугольник плюс трапеция невозможно.

В таблице для примера и выбора основных показателей для построения треугольника и трапеции приведены некоторые численные значения переменных, входящих в уравнения. С ее помощью можно задать отношение S/а и получить отношение h/t.

На рис. 1 представлено решение задачи предлагаемым методом. В качестве примера, не имеющего принципиального значения, взято равенство высот треугольника и трапеции. Для большей наглядности на рисунке приведены дополнительные геометрические построения: деление угла надвое, проведение параллельных линий и нанесение равномерных делений.

Решение задачи начинается с деления заданного угла АВС пополам линией ВЕ и проведения под прямым углом к ней через точку В горизонтальной линии XY. На линии ХY в обе стороны от точки В наносятся деления, отвечающие отношению основания трапеции к ее стороне, в данном случае 5 и 2. Это соотношение получено из уравнения (2) при условии равенства высот - см. таблицу.

Из точек, отвечающих делению 5, проводятся параллели биссектрисе ВЕ до пересечения со сторонами угла в точках А и С. Линия АС служит общим основанием треугольника и трапеции, отрезки АВ и ВС равны. Из точек, отвечающих отметке 2 на отрезке XY, проводятся линии, также параллельные биссектрисе угла АВС, и на них отрезками BD и BF, равными сторонам треугольника ВА = ВС, отмечаются точки D и F - вершины углов трапеции АDFC. Точки D и F определяют высоту ВЕ, равную сумме высот треугольника и трапеции.

Для проверки и доказательства проводятся диагонали AF и DC трапеции АDFC, пересекающиеся в точке Z на средней линии треугольника АВС. Образовавшиеся два треугольника АDF и DFC равнобедренные, поскольку их основания, т. е. диагонали трапеции, разделены в точках Т надвое, пересекаясь в них с радиусами ВD и ВF и средней линией РР трапеции. Сторона DF принадлежит обоим треугольникам, поэтому треугольники АВD, DВF и FВС равны. Все три их угла с вершинами в точке В равны между собой и в сумме составляют заданный угол АВС.

Отрезки прямых DM и FN образуют стороны ромбов ADFN и DFCM, своими геометрическими свойствами подтверждающих правильность построения.

На рис. 2 показано соотношение образовавшихся углов. Характерно, что нижние углы трапеции DАС = FСА равны одной трети разделяемого угла АВС.

При построении геометрической фигуры на рис. 1 было принято отношение величины основания трапеции к ее стороне 5:2 для простоты построений: этому соотношению отвечает равенство высот трапеции и треугольника.

На рис. 3 построена фигура "треугольник - трапеция" для сравнительно острого угла АВС. Исходным принимается отношение высоты треугольника к сумме высот треугольника и трапеции, равное 5:6, которому, согласно уравнению (1), отвечает значение S/а = 17/6. Как и в первом случае, это значение поровну, т. е. 8 1/2 к 3, откладывается на линии XY в обе стороны от точки В, и производятся аналогичные построения.

Вообще, нет необходимости предварительно принимать численные значения S/а. Достаточно на линиях ВХ и ВY из точки В отложить по три равных отрезка, отметив их концы, и из любой точки между второй и третьей отметками построить перпендикуляры до пересечения со сторонами угла В в точках А и С. Затем из первой отметки также восстановить перпендикуляры и на них отложить точки D и F на расстоянии от точки В, равном стороне треугольника АВС.

Если из точек А и С на линиях ВD и ВF отложить по две равноотстоящие точки N и М, получим отрезок NM, равный S-2а. Отношение этой длины к а определяет отношение высот трапеции и треугольника согласно формуле (2).

В остальном поступают, как и в первом случае. Правильность построения можно проверить по формуле

следующей из (2). Сумма t+h никогда не превышает сторону ВА(ВD) треугольника.

Графически равенство (4) проверяется так (рис. 4). Берется произвольный угол PQN, разделенный биссектрисой QQ?. На левой стороне угла от точки Q циркулем откладываются отрезки S-а и а, образующие точки Р и L. Далее точка Р соединяется с точкой Q? и из точки L проводится параллельная РQ? линия LQ. Это означает, что на биссектрисе угла возникла отметка Q, причем а/(S-а)= = QQ??/QQ?. На правой стороне угла откладываем циркулем отрезки 2t+h и t+h из построенного чертежа. Конец отрезка 2t+h - точку N - также соединяем с точкой Q?, а из точки М - конца отрезка t+h - проводим линию, параллельную NQ?. На средней линии угла отмечается отношение (t+h)/(2t+h)=QQ. /QQ?. Если линии LQ?? и МQ. пересекаются на средней линии угла, это означает, что левая и правая части в формуле равны. Что и требуется.

Можно ли путем измерения соответствующих отрезков, в частности оснований треугольников, определить их длину? Нельзя, так как каждый служит хордой соответствующей воображаемой дуги окружности, содержащей долю, не поддающуюся измерению. Для определения точности решения задачи может быть использован только графический метод.

Таким образом, нами предложено доказательство возможности графического деления угла на три с помощью циркуля и линейки. Остается графически не выясненной связь элементов трапеции и треугольников, иными словами, зависимость между стороной трапеции а и высотой треугольника t. Эта задача может иметь самостоятельный характер для принципа построения трапеции.

Приношу благодарность профессору МГТУ В. И. Солонину за благожелательную критику.

№ слайда 1

Математика и проектирование Проект по теме: “Трисекция угла” Выполнила: ученица 8 класса В МОУ СОШ № 13 г.Тамбова Бакушкина Маргарита Александровна Учитель: Кирина Елена Викторовна Адрес: 392032 г.Тамбов Б.-Энтузиастов, 30 В кв. 24 Д.т. (4752) 45 54 94 e-mail: [email protected]

№ слайда 2

Цели: познакомиться с историей развития решения задачи деления угла на три равные части; поиск решения задачи наиболее удобным способом; сконструировать циркуль – трисектор.

№ слайда 3

Краткое содержание: Вступление; Постановка проблемы; Исторические сведения; Методы доказательства; Решение задачи о трисекции угла циркулем и линейкой; Простейший трисектор; Циркуль- трисектор; Практическое применение циркуля – трисектора; Вывод; Литература.

№ слайда 4

Вступление. Задачи на геометрические построения – одни из самых популярных в школьной математике. История геометрических построений насчитывает несколько тысяч лет, и уже древние достигли здесь большого искусства. Нам известны 3 знаменитые задачи древности: о квадратуре круга, трисекции угла и удвоении куба. Лишь в конце прошлого века была доказана их неразрешимость. В своей работе я рассмотрела задачу о трисекции угла. Она возникла из потребностей архитектуры и строительной техники. При составлении рабочих чертежей, разного рода украшений, многогранных колоннад, при строительстве, внутренней и внешней отделки храмов, надгробных памятников древние инженеры, художники встретились с необходимостью уметь делить окружность на три равные части, а это часто вызывало затруднения.

№ слайда 5

Постановка проблемы.С глубокой древности известна одна из знаменитых задач древности – задача о трисекции угла. Она сыграла важную роль в истории математики. В конце концов было доказано, что эту задачу невозможно решить, пользуясь только циркулем и линейкой. Но уже сама постановка задачи - “доказать неразрешимость” – была смелым шагом вперёд. Вместе с тем предлагалось множество решений при помощи нетрадиционных инструментов. Всё это привело к возникновению и развитию совершенно новых идей в геометрии и алгебре. Немало преуспели в нестандартных и различных приближённых решениях любители математики. Задача кажется доступной любому: вводит в заблуждение простая формулировка.

№ слайда 6

Исторические сведения.Платон. Платон, живший в 428 – 328 годах до нашей эры, считается одним из величайших философов Греции. Геометрия ко времени Платона уже была очень развита. Было решено много весьма и весьма сложных задач, доказаны сложнейшие теоремы. В конце прошлого века было доказано, что в такой постановке данная задача не может быть решена, хотя, если использовать другие геометрические инструменты или использовать при построении геометрические места точек, отличные от прямой, либо дуги окружности. То эта задача легко решается. Однако принятые у греков правила игры не позволяли пользоваться при решении задачи ничем, кроме циркуля и линейки. Платон даже обосновал это ссылкой на авторитет богов. Так что проблема решена не была, но по ходу дела геометрия была основательно разработана.

№ слайда 7

Архимед. Архимед (?287-212 гг. до нашей эры) родился в городе Сиракузы на острове Сицилия. Он автор многочисленных открытий, гениальный изобретатель, известный во всем греческом мире благодаря конструкции многих механизмов: машины для орошения полей, водоподъемного механизма, системы рычагов, блоков для поднятия больших тяжестей (кранов), военных метательных аппаратов. Он соорудил систему блоков, с помощью которой один человек смог спустить на воду огромный корабль "Сиракосия". Крылатыми стали произнесенные тогда слова Архимеда: "Дайте мне точку опоры, и я поверну Землю". Архимед погиб от меча римского легионера. На своей могильной плите Архимед завещал выгравировать шар и цилиндр - символы его геометрических открытий.

№ слайда 8

Методы доказательства.Существуют различные способы построения трисектрисы угла: При помощи циркуля и линейки без засечек (трисекция угла в 900, 450, 22,50. p /2n, где nI N (все эти углы образуют бесконечно малую геометрическую прогрессию со знаменателем q =1/2),трисекция угла в 1800,3600). Квадратрисса Гиппея; Конхоида Никомеда; Спираль Архимеда; С помощью простейшего трисектора; При помощи циркуля-трисектора.

№ слайда 9

Решение задачи о трисекции угла циркулем и линейкой. Пусть на чертеже отрезок AB равен радиусу окружности: AB =OB=OC=OD. Тогда (угол CBO – внешний угол треугольника ABO), (как внешний угол треугольника ACO). Отсюда вытекает следующий способ деления произвольного угла на три равные части. Сделаем на линейке две отметки A и B. Радиусом AB опишем окружность с центром в вершине O данного угла (который нужно разделить на три части). Точки пересечения её со сторонами угла обозначим C и D. Будем двигать линейку так, чтобы её край всё время проходил через точку C, а точка A скользила по прямой OD, пока точка B не попадёт на окружность. Когда это произойдёт, мы получим расположение, изображённое на чертеже, так что угол BAO окажется равным 1/3 угла COD. Прямая OM параллельна AC, , а угол COM разделим с помощью циркуля пополам.

№ слайда 10

Простейший трисектор. На сегодняшний день придумано много механических способов для построения трисектрисы угла. Такие приборы называются трисекторами. Простейший трисектор можно легко изготовить из плотной бумаги, картона или тонкой жести. Он будет служить подсобным чертежным инструментом. На чертеже трисектор изображен в натуральную величину (заштрихованная фигура). Примыкающая к полукругу полоска AB равна длине радиуса полукруга. Край полоски BD составляет прямой угол с AC; он касается полукруга в точке B; длина полоски BD произвольная. На этом же рисунке показано применение трисектора. Например, требуется разделить угол KSM. Поместим трисектор так, чтобы вершина угла S находилась на линии BD, одна сторона угла прошла через точку A, а другая сторона коснулась полукруга. Возможность такого вложения нашего трисектора в данный угол является следствием одного простого свойства точек лучей, делящих данный угол на 3 равные части: если из любой точки O луча SO провести отрезки , то будем иметь: AB=OB=ON. Затем проведём прямые SB и SO, и деление данного угла на 3 равные части закончено.

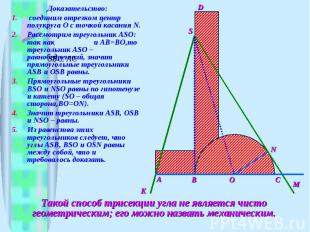
№ слайда 11

Доказательство: соединим отрезком центр полукруга O с точкой касания N. Рассмотрим треугольник ASO: так как и AB=BO,то треугольник ASO – равнобедренный, значит прямоугольные треугольники ASB и OSB равны. Прямоугольные треугольники BSO и NSO равны по гипотенузе и катету (SO – общая сторона,BO=ON). Значит треугольники ASB, OSB и NSO – равны. Из равенства этих треугольников следует, что углы ASB, BSO и OSN равны между собой, что и требовалось доказать. Такой способ трисекции угла не является чисто геометрическим; его можно назвать механическим.

№ слайда 12

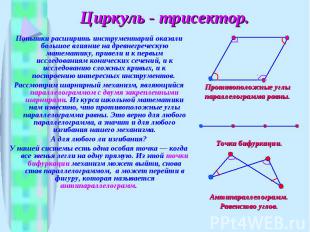
Циркуль - трисектор. Попытки расширить инструментарий оказали большое влияние на древнегреческую математику, привели и к первым исследованиям конических сечений, и к исследованию сложных кривых, и к построению интересных инструментов. Рассмотрим шарнирный механизм, являющийся параллелограммом с двумя закрепленными шарнирами. Из курса школьной математики нам известно, что противоположные углы параллелограмма равны. Это верно для любого параллелограмма, а значит и для любого изгибания нашего механизма. А для любого ли изгибания? У нашей системы есть одна особая точка — когда все звенья легли на одну прямую. Из этой точки бифуркации механизм может выйти, снова став параллелограммом, а может перейти в фигуру, которая называется антипараллелограмм.

№ слайда 13

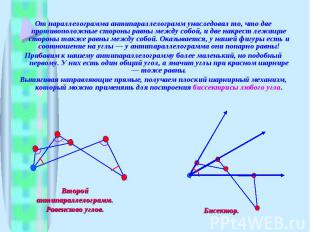
От параллелограмма антипараллелограмм унаследовал то, что две противоположные стороны равны между собой, и две накрест лежащие стороны также равны между собой. Оказывается, у нашей фигуры есть и соотношение на углы — у антипараллелограмма они попарно равны! Прибавим к нашему антипараллелограмму более маленький, но подобный первому. У них есть один общий угол, а значит углы при красном шарнире — тоже равны. Вытягивая направляющие прямые, получаем плоский шарнирный механизм, который можно применять для построения биссектрисы любого угла.

№ слайда 14

Можно прибавить еще один подобный антипараллелограмм. По тем же соображениям его угол при красном шарнире будет равен уже двум имеющимся. Получившийся плоский шарнирный механизм является трисектором углов — решает задачу о делении произвольного угла на три равные части! Однако, очевидно, использованный алгоритм построения можно продолжать и дальше, получая шарнирные механизмы, точно делящие произвольный угол на любое наперед заданное число частей.

№ слайда 15

Практическое применение циркуля- трисектора.

№ слайда 16

Вывод При выяснении возможности планиметрической задачи на построение пользуются следующим критерием: построение отрезка циркулем и линейкой возможно тогда и только тогда, когда его длина выражается через длины данных отрезков в виде конечной комбинации четырёх арифметических действий и извлечения арифметического квадратного корня. С помощью этого критерия доказано, что знаменитая задача древности – трисекция угла- неразрешима с помощью циркуля и линейки. Работая над проектом я исследовала способы построения трисектрисы угла и сконструировала простейший трисектор.

Трисекция угла

Работу выполнили: Шаронова Оксана ученица 10Б класса, Банчукова Ольга ученица 10 Б класса

Цель работы:

Выяснить, как можно разделить угол на три равные части, обходясь при этом без циркуля и линейки.

История вопроса:

Задачу трисекции угла пытались решить ещё в V в. до н.э. в Греции. Никомед из Александрии (II в.до н.э.) использовал для решения этой задачи особую кривую—конхоиду. Свои методы и способы решения этой задачи предлагали Виет, Архимед, Гиппий Элитский (его квадратиса). Французский математик П.Ванцель в 1837 г. первым строго доказал, что невозможно осуществить трисекцию циркулем и линейкой. Но математика вовсе не отвергает возможность выполнить это деление при помощи каких-либо иных приборов. Придумано много механических приборов для достижения указанной цели. Такие приборы называются трисекторами.

Простейший трисектор

Трисектор устроен следующим способом: примыкающая к полукругу полоска АВ равна по длине радиусу полукруга. Край полоски ВD составляет прямой угол с прямой АС; он касается полукруга в точке В; длина этой полоски произвольна.

Применение трисектора

Трисектор поместим внутри угла КSМ так, чтобы вершина угла S находилась на линии ВD, одна сторона угла прошла через точку А, а другая сторона коснулась полукруга.

Доказательство:

Отрезки ON и OS перпендикулярны. ?ASB=?OSB, т. к. у них АВ=ОВ, SВ– общая сторона, углы АВS и OBS прямые. ?OSB=?OSN, т.к. у них ОВ=ОN, OS - общая сторона, углы SBO и SNO равны. Значит, ?ASB=?OSB=?OSN. Отсюда следует, что углы ASB, BSO и OSN равны. Что и требовалось доказать.

Часы-трисектор

Рассмотрим применение обыкновенных часов для деления угла на три равные части. Для этого надо перевести фигуру данного угла на прозрачную бумагу и в тот момент, когда обе стрелки часов совмещаются , наложить чертеж на циферблат так, чтобы вершина угла совпала с центром вращения стрелок и одна сторона угла пошла вдоль стрелок.

Часы-трисектор

В тот момент, когда минутная стрелка часов передвинется до совпадения с направлением второй стороны данного угла, провести из вершины угла луч по направлению часовой стрелки. Образуется угол, равный углу поворота часовой стрелки. Теперь при помощи циркуля и линейки надо удвоить этот угол , а удвоенный угол снова удвоить. Полученный таким образом угол и будет составлять 1/3 данного.

Вывод:

В ходе работы мы выяснили, что разделение угла на три равные части без циркуля и линейки возможно, но этот способ является небезупречно точным, а только механическим.

Список использованной литературы:

Перельман Я.И. Занимательная геометрия. – Д.: ВАП 1994г. Прохоров Ю.В. Большой Энциклопедический Словарь. – М.: Большая Российская энциклопедия. 1998г.

Читайте также: