Как сделать треугольник паскаля в excel
Добавил пользователь Алексей Ф. Обновлено: 07.10.2024
Треугольник Паскаля — элегантный математический треугольник, представляющий собой бесконечную таблицу биноминальных коэффициентов. Таблица иллюстрирует скрытые соотношения между числами, которые естественным образом возникают в теории чисел, комбинаторике, теории вероятностей и алгебре.
Суть треугольной последовательности
Число 1 — важное число, а 11? Любопытно, что 11 x 11 = 121, 11 x 11 x 11 = 1331, а 11 x 11 x 11 x 11 = 14641. Если выстроить эти числа сверху вниз и представить их в виде отдельных цифр, то получится интересная формация:
Эти цифры — первые строки знаменитого треугольника Паскаля. Далее таблица строится по следующему принципу: по краям записываются единицы, а внутри ряда числа формируются путем суммы цифр, расположенных рядом выше слева и справа от искомых. Данная таблица знаменита в математике своей элегантностью, симметрией и неожиданными связями между числами. Связи таблицы с другими математическими сферами превратили треугольник Паскаля в Священный Грааль математики.
История открытия
Удивительные свойства
Симметрия — очевидное свойство треугольника Паскаля. Если из верхней единицы провести вертикальную прямую, то числа справа и слева будут симметричны. Диагонали треугольника также симметричны. Диагонали вообще обладают рядом уникальных свойств. Если первая диагональ, как восточная, так и западная, представляет собой ряд сплошных единиц, то вторая — ряд натуральных чисел, третья — ряд треугольных чисел, а четвертая — тетраэдрических.
- Треугольные числа (1, 3, 6, 10…) — это числа, при помощи которых строятся плоские треугольники. Простыми словами, если в двухмерной игре вы захотите составить треугольник из круглых элементов, то вам понадобится выстроить элементы в количестве, советующему треугольным числам: сначала 6 кругов, потом 3, потом 1.
- Тетраэдрические числа (1, 4, 10, 20…) используются для построения объемных тетраэдров. Проще говоря, если вам понадобится сложить пушечные ядра аккуратной пирамидой, то в основании вам потребуется уложить 20 ядер, на них еще 10, сверху 4 и увенчать пирамиду одним верхним ядром.
Кроме того, если в треугольнике Паскаля четные числа заменить единицами, а нечетные — нулями, то получится треугольник Серпинского — известный фрактал, построенный польским математиком в начале 20 века.
Треугольник Паскаля также имеет удивительную связь с алгеброй. Если мы разложим бином Ньютона вида (1 + x) 2 , то получим 1 + 2x + x 2 . Если же это будет (1 + x) 3 , то в результате мы получим 1 + 3x + 3x 2 + x 3 . Если присмотреться, то биноминальные коэффициенты — это ни что иное как числа из соответствующего ряда треугольника Паскаля.
Построение треугольника Паскаля
Треугольник Паскаля — это бесконечная таблица элементов. При помощи нашего калькулятора вы можете построить таблицу любой размерности, однако не рекомендуется использовать слишком большие числа (n>100), так как столь огромные таблицы не имеют практического применения, а онлайн-калькулятор строит их слишком долго. Помимо элегантных свойств, используемых для решения биноминальных уравнений или построения тетраэдрических последовательностей, таблица Паскаля находит применение в комбинаторике.
Примеры из реальной жизни
Подсчет количества способов
Для ответа на вопрос нам достаточно построить треугольник с n = 10, найти седьмой ряд и третье число в нем. Таким образом, существует 35 способов объединить математиков для поездки на олимпиаду.
Определение вероятности
В корзине лежит 20 шаров, пронумерованных от 1 до 20. Наугад мы берем 3 шара. Какова вероятность, что мы вытащим шары с номерами 5, 12 и 13? Для решения этой задачи нам потребуется построить треугольник Паскаля с n = 20, после чего найти двадцатый ряд и третье число в нем. Вытащить три шара можно 1140 способами. Вероятность наступления нашего события составит 3 из 1140.
Заключение
Треугольник Паскаля — простая таблица, которая таит в себе огромное количество математических тайн. Члены рядов связаны с биноминальными коэффициентами, совершенными числами, числами Фибоначчи, тетраэдрическими и треугольными числами. Используйте наш калькулятор для построения сетки необходимой вам размерности для решения самых разных математических задач.
В дополнение к возможности поддержки вычислений в Excel также есть инструменты, которые упрощают пользователям использование инструментов рисования. В этой статье я расскажу вам, как рисовать равносторонние треугольники в Excel 2013.

Шаг 2: Нажмите и удерживайте клавишу Shift, перемещая мышь, чтобы настроить размер. Когда будет похоже, что вы хотите отпустить кнопку мыши.
С помощью простой операции вы начертите равносторонний треугольник.
Основные операции с треугольниками
1. Измените размер, направление вращения.
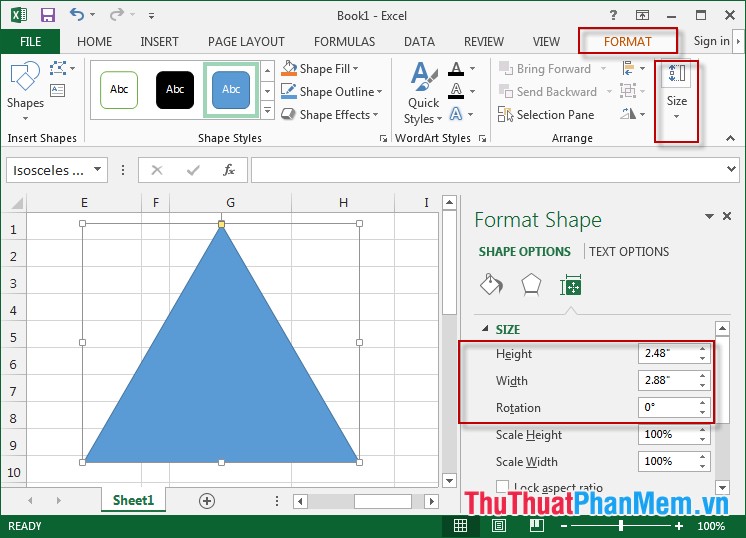
2. Залейте фон треугольником.
Перейдите на вкладку Формат -> Заливка фигуры -> выберите соответствующий цвет.

3. Выберите цвет обводки равносторонних треугольников.

4. Создавайте эффекты.
Треугольником Паскаля называется бесконечная треугольная таблица, в которой на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей строке.
| № | Треугольник Паскаля |
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| … | … |
Треугольник Паскаля можно получить из таблицы натуральных степеней бинома x + y
Натуральные степени бинома x + y
| № | Степень | Разложение в сумму одночленов |
| 0 | (x + y) 0 = | 1 |
| 1 | (x + y) 1 = | 1x + 1y |
| 2 | (x + y) 2 = | 1x 2 + 2xy + 1y 2 |
| 3 | (x + y) 3 = | 1x 3 + 3x 2 y + 3xy 2 + 1y 3 |
| 4 | (x + y) 4 = | 1x 4 + 4x 3 y + 6x 2 y 2 + 4xy 3 + 1y 4 |
| 5 | (x + y) 5 = | 1x 5 + 5x 4 y + 10x 3 y 2 + 10x 2 y 3 + 5xy 4 + 1y 5 |
| 6 | (x + y) 6 = | 1x 6 + 6x 5 y + 15x 4 y 2 + 20x 3 y 3 + 15x 2 y 4 + 6xy 5 + 1y 6 |
| … | … | … |
Свойства треугольника Паскаля
- Сумма чисел n-ной строки (отсчет ведется с нуля) треугольника Паскаля равна 2 n . Действительно, при переходе от каждой строки к следующей сумма членов удваивается, а для нулевой строки она равна 2 0 =1 .
- Все строки треугольника Паскаля симметричны. Потому что при переходе от каждой строки к следующей свойство симметричности сохраняется, а нулевая строка симметрична.
- Каждое число в треугольнике Паскаля равно Cn k , где n - номер строки, k - номер (отсчет ведется с нуля) элемента в строке.
- Каждое число треугольника Паскаля, уменьшенное на единицу, равно сумме всех чисел, заполняющих параллелограмм, ограниченный диагоналями, на пересечении которых находится этот элемент.
- Вдоль диагоналей, параллельных сторонам треугольника, выстроены треугольные числа, тетраэдрические числа и т.д.
- Если посчитать для каждой восходящей диагонали треугольника Паскаля сумму всех стоящих на этой диагонали чисел, то получится соответствующее число Фибоначчи.
Определения
Треугольными числами называется количество шаров, которые можно выложить в виде равностороннего треугольника.
Тетраэдрическими числами называется количество шаров, которые можно выложить в виде правильного тетраэдра.
Последовательность f1 = f2 = 1 , fn = fn-1 + fn-2 при n>2 называется последовательностью Фибоначчи, а ее члены — числами Фибоначчи.
Написать разложение вида: (x + y) 7
Воспользовавшись строкой треугольника Паскаля с номером 6 и применив основное свойство треугольника Паскаля, получим строку с номером 7:
Треугольник Паскаля назван в честь французского математика Блеза Паскаля . Это треугольный массив биномиальных коэффициентов.
Треугольник следует очень простому правилу.
Каждое число представляет собой сумму двух чисел, расположенных непосредственно над ним.
Вот gif, который иллюстрирует заполнение треугольника Паскаля.
Значение элемента (i,j) задается C(i,j)!/((i-j)!*j!) . Где i-номер строки, а j – позиция элемента в этой строке.
Java – код для треугольника Паскаля
Код Java для печати треугольника паскаля выглядит следующим образом.
Код вводит количество строк треугольника паскаля от пользователя.
Давайте пройдемся по коду и разберемся.
Разбивка Кода
Самый внешний для цикла отвечает за печать каждой строки. Он будет запускать “строку” несколько раз.
Следующий цикл для отвечает за печать пробелов в начале каждой строки.
Мы видим, что по мере увеличения текущего номера строки ( i ) количество запусков этого цикла будет уменьшаться.
Следующий цикл для отвечает за печать чисел в треугольнике.
Для первой строки и первого элемента каждой последующей строки в качестве выходных данных выводится 1.
Формула, которая вычисляет цифру для оставшихся позиций, выглядит так:
Где i-номер текущей строки, а j-позиция элемента в этой строке.
j инициализируется значением 0 для каждой строки.
Мы можем провести быструю сухую пробежку для строки № 3.
Ряд получается таким:
Вы также должны сделать это для строк 4 и 5, чтобы понять, как работает формула.
Чтобы правильно отформатировать вывод, мы используем printf.
Выход
Результат, полученный после выполнения кода, выглядит следующим образом:
Вывод
Этот учебник был посвящен треугольнику паскаля и тому, как написать код для его создания. Надеюсь, вы поняли концепцию и получили удовольствие, узнав о ней!

Читайте также:
 webdonsk.ru
webdonsk.ru