Как сделать транспонированную матрицу

Добавил пользователь Алексей Ф.
Обновлено: 02.09.2024

Пусть — произвольные матрицы, для которых определены операции умножения и сложения, записанные в левых частях следующих равенств. Тогда определены операции, указанные в правых частях, и справедливы равенства:

Пример 1.18. Найти транспонированные матрицы , если

Решение. Согласно определению, при транспонировании первая строка матрицы Аналогично находим

Так как — симметрическая.

Пример 1.19. Продемонстрировать справедливость свойств 1, 2, 3, 4, если

Решение. Продемонстрируем свойство 1: . Вычисляя левую и правую части, получаем равные матрицы

Продемонстрируем свойство 2: . Вычисляя левую и правую части, получаем равные матрицы

Продемонстрируем свойство 3: . Вычисляя левую и правую части, получаем равные матрицы:

Продемонстрируем свойство 4: . Вычисляя левую часть, получаем правую:

Пример 1.20. Пусть — симметрические, а матрица — кососимметрическая.

Решение. По свойствам 3,4 получаем:

Сопряжение матриц

Пусть ( комплексная матрица ). Сопряженной матрицей , получаемая из матрицы эрмитовой , если Пример 1.21. Даны матрицы и . Найти сопряженные матрицы .

Решение. Найдем транспонированные матрицы:

Заменим все элементы сопряженными:

Заметим, что матрица — эрмитова, так как .

Свойства операции сопряжения матриц

где — произвольные матрицы, для которых определены соответствующие операции, — любое комплексное число, — сопряженное к Пример 1.22. Продемонстрировать справедливость свойств 1, 2, 3, 4, если

Решение. 1. Вычисляем и сравниваем левую и правую части равенства 1:

2. Вычисляем и сравниваем левую и правую части равенства 2:

3. Вычисляем и сравниваем левую и правую части равенства

4. Вычисляем левую часть равенства 4 и сравниваем ее с правой частью:

1. Если все элементы матрицы действительная матрица ), то сопряженная матрица совпадает с транспонированной, т.е. .

2. Всякую комплексную матрицу (с элементами ) можно представить в виде , где действительная и мнимая части матрицы (с элементами и соответственно). При этом сопряженную матрицу можно представить в виде 3. Всякую эрмитову матрицу можно представить в виде , где , а . В самом деле, из равенства , учитывая пункт 2, следует, что . Равенство действительных частей дает

Пример 1.23. Пусть — эрмитовы m-го и n-го порядков соответственно.

Решение. Используя свойства 3, 4, получаем:

что и требовалось доказать.

1. Эрмитова матрица с действительными элементами является симметрической.

2. Элементы эрмитовой матрицы, стоящие на главной диагонали, действительны (например, матрица в примере 1.21).

След матрицы

Следом квадратной матрицы называется сумма ее элементов, стоящих на главной диагонали. След квадратной матрицы

Для любых квадратных матриц n-го порядка и столбцов размеров справедливы следующие свойства:

Замечание 1.6. След матрицы также обозначается .

Пример 1.24. Даны квадратные матрицы и столбцы . Продемонстрировать справедливость свойств 1, 2, 3, 4, 5, 7.

Кроме сложения, вычитания и умножения матриц существует еще операция над матрицами, которая называется транспонированием матрицы. Полученная в результате данной операции матрица называется транспонированной и обозначается $A^ $.

Транспонированная матрица -- это матрица, которая получается из исходной матрицы А путем перестановки строк и столбцов.

Исходя из определения можно записать следующее: пусть дана матрица $A=\left(a_ \right)_ $, тогда транспонированная матрица будет иметь вид $A^ =\left(a_ \right)_ $.

Другими словами, чтобы получить транспонированную матрицу, необходимо взять каждую строчку по очереди и переписать ее в виде столбца, не меняя порядка следования.

Определение. Пусть задана матрица $A.$ Тогда замена строк на столбцы, а столбцов — на строки называется транспонированием по отношению к $A.$ Так, если $$A = \begin
a_ & a_ & \cdots & a_\\
a_ & a_ & \cdots & a_\\
\cdots & \cdots & \cdots & \cdots\\
a_ & a_ & \cdots & a_
\end,$$ то транспонированная матрица будет выглядеть: $$A^ = \begin
a_ & a_ & \cdots & a_\\
a_ & a_ & \cdots & a_\\
\cdots & \cdots & \cdots & \cdots\\
a_ & a_ & \cdots & a_
\end.$$

Свойства транспонирования матриц

Пусть задана матрица $$A = \begin
a_ & a_ & \cdots & a_\\
a_ & a_ & \cdots & a_\\
\cdots & \cdots & \cdots & \cdots\\
a_ & a_ & \cdots & a_
\end.$$
Проведём транспонирование матрицы $A:$
$$A^ = \begin
a_ & a_ & \cdots & a_\\
a_ & a_ & \cdots & a_\\
\cdots & \cdots & \cdots & \cdots\\
a_ & a_ & \cdots & a_
\end.$$
Проведём повторное транспонирование матрицы $A^$ и получаем: $$\left ( A^ \right )^ = \begin
a_ & a_ & \cdots & a_\\
a_ & a_ & \cdots & a_\\
\cdots & \cdots & \cdots & \cdots\\
a_ & a_ & \cdots & a_
\end. $$
Следовательно, $ \left ( A^ \right )^ = A,$ что и требовалось доказать.

Пусть задана матрица $$A = \begin
a_ & a_ & \cdots & a_\\
a_ & a_ & \cdots & a_\\
\cdots & \cdots & \cdots & \cdots\\
a_ & a_ & \cdots & a_
\end.$$
Проведём транспонирование матрицы $A:$
$$A^ = \begin
a_ & a_ & \cdots & a_\\
a_ & a_ & \cdots & a_\\
\cdots & \cdots & \cdots & \cdots\\
a_ & a_ & \cdots & a_
\end.$$
Докажем, что $ \left ( \lambda \cdot A \right )^ = \lambda \cdot A^.$ Найдём $\left ( \lambda \cdot A \right )^$ $$ \lambda \cdot \begin
a_\cdot & a_ & \cdots & a_\\
a_ & a_ & \cdots & a_\\
\cdots & \cdots & \cdots & \cdots\\
a_ & a_ & \cdots & a_
\end = \begin
a_\cdot \lambda & a_\cdot \lambda & \cdots & a_\cdot \lambda\\
a_\cdot \lambda & a_\cdot \lambda & \cdots & a_\cdot \lambda\\
\cdots & \cdots & \cdots & \cdots\\
a_\cdot \lambda & a_\cdot \lambda & \cdots & a_\cdot \lambda
\end.$$
Проведём транспонирование и получаем: $$\left ( \lambda \cdot A \right )^ = \begin
a_\cdot \lambda & a_\cdot \lambda & \cdots & a_\cdot \lambda\\
a_\cdot \lambda & a_\cdot \lambda & \cdots & a_\cdot \lambda\\
\cdots & \cdots & \cdots & \cdots\\
a_\cdot \lambda & a_\cdot \lambda & \cdots & a_\cdot \lambda
\end. $$
Найдём $\lambda \cdot A^:$ $$ \lambda \cdot A^ = \begin
a_\cdot \lambda & a_\cdot \lambda & \cdots & a_\cdot \lambda\\
a_\cdot \lambda & a_\cdot \lambda & \cdots & a_\cdot \lambda\\
\ldots & \cdots & \cdots & \cdots\\
a_\cdot \lambda & a_\cdot \lambda & \cdots & a_\cdot \lambda
\end.$$
Следовательно, $\left ( \lambda \cdot A \right )^ = \lambda \cdot A^,$ что и требовалось доказать.

Примеры решения задач

Пример 1

Дана матрица $ A = \begin
5 & 2 & 6 \\
1 & 4 & 9 \\
8 & 3 & 10
\end.$ Составить матрицу $A^.$

В этой теме будут рассмотрены такие операции, как сложение и вычитание матриц, умножение матрицы на число, умножение матрицы на матрицу, транспонирование матрицы. Все обозначения, которые используются на данной странице, взяты из предыдущей темы "Матрицы. Виды матриц. Основные термины".

Сложение и вычитание матриц.

Аналогичное определение вводят и для разности матриц:

Запись "$i=\overline$" означает, что параметр $i$ изменяется от 1 до m. Например, запись $i=\overline$ говорит о том, что параметр $i$ принимает значения 1, 2, 3, 4, 5.

Стоит обратить внимание, что операции сложения и вычитания определены только для матриц одинакового размера. Вообще, сложение и вычитание матриц – операции, ясные интуитивно, ибо означают они, по сути, всего лишь суммирование или вычитание соответствующих элементов.

Заданы три матрицы:

Можно ли найти матрицу $A+F$? Найти матрицы $C$ и $D$, если $C=A+B$ и $D=A-B$.

Матрица $A$ содержит 2 строки и 3 столбца (иными словами – размер матрицы $A$ равен $2\times 3$), а матрица $F$ содержит 2 строки и 2 столбца. Размеры матрицы $A$ и $F$ не совпадают, поэтому сложить их мы не можем, т.е. операция $A+F$ для данных матриц не определена.

Размеры матриц $A$ и $B$ совпадают, т.е. данные матрицы содержат равное количество строк и столбцов, поэтому к ним применима операция сложения.

$$ C=A+B=\left(\begin -1 & -2 & 1 \\ 5 & 9 & -8 \end \right)+ \left(\begin 10 & -25 & 98 \\ 3 & 0 & -14 \end \right)=\\= \left(\begin -1+10 & -2+(-25) & 1+98 \\ 5+3 & 9+0 & -8+(-14) \end \right)= \left(\begin 9 & -27 & 99 \\ 8 & 9 & -22 \end \right) $$

Найдем матрицу $D=A-B$:

Ответ: $C=\left(\begin 9 & -27 & 99 \\ 8 & 9 & -22 \end \right)$, $D=\left(\begin -11 & 23 & -97 \\ 2 & 9 & 6 \end \right)$.

Умножение матрицы на число.

Произведением матрицы $A_=(a_)$ на число $\alpha$ называется матрица $B_=(b_)$, где $b_=\alpha\cdot a_$ для всех $i=\overline$ и $j=\overline$.

Попросту говоря, умножить матрицу на некое число – означает умножить каждый элемент заданной матрицы на это число.

Задана матрица: $ A=\left(\begin -1 & -2 & 7 \\ 4 & 9 & 0 \end \right)$. Найти матрицы $3\cdot A$, $-5\cdot A$ и $-A$.

$$ 3\cdot A=3\cdot \left(\begin -1 & -2 & 7 \\ 4 & 9 & 0 \end \right) =\left(\begin 3\cdot(-1) & 3\cdot(-2) & 3\cdot 7 \\ 3\cdot 4 & 3\cdot 9 & 3\cdot 0 \end \right)= \left(\begin -3 & -6 & 21 \\ 12& 27 & 0 \end \right).\\ -5\cdot A=-5\cdot \left(\begin -1 & -2 & 7 \\ 4 & 9 & 0 \end \right) =\left(\begin -5\cdot(-1) & -5\cdot(-2) & -5\cdot 7 \\ -5\cdot 4 & -5\cdot 9 & -5\cdot 0 \end \right)= \left(\begin 5 & 10 & -35 \\ -20 & -45 & 0 \end \right). $$

Запись $-A$ есть сокращенная запись для $-1\cdot A$. Т.е., чтобы найти $-A$ нужно все элементы матрицы $A$ умножить на (-1). По сути, это означает, что знак всех элементов матрицы $A$ изменится на противоположный:

$$ -A=-1\cdot A=-1\cdot \left(\begin -1 & -2 & 7 \\ 4 & 9 & 0 \end \right)= \left(\begin 1 & 2 & -7 \\ -4 & -9 & 0 \end \right) $$

Произведение двух матриц.

Определение этой операции громоздко и, на первый взгляд, непонятно. Поэтому сначала укажу общее определение, а потом подробно разберем, что оно означает и как с ним работать.

Произведением матрицы $A_=(a_)$ на матрицу $B_=(b_)$ называется матрица $C_=(c_)$, для которой каждый элемент $c_$ равен сумме произведений соответствующих элементов i-й строки матрицы $A$ на элементы j-го столбца матрицы $B$: $$c_=\sum\limits_^a_b_, \;\; i=\overline, j=\overline.$$

Пошагово умножение матриц разберем на примере. Однако сразу стоит обратить внимание, что перемножать можно не все матрицы. Если мы хотим умножить матрицу $A$ на матрицу $B$, то сперва нужно убедиться, что количество столбцов матрицы $A$ равно количеству строк матрицы $B$ (такие матрицы часто называют согласованными). Например, матрицу $A_$ (матрица содержит 5 строк и 4 столбца), нельзя умножать на матрицу $F_$ (9 строк и 8 столбцов), так как количество столбцов матрицы $A$ не равно количеству строк матрицы $F$, т.е. $4\neq 9$. А вот умножить матрицу $A_$ на матрицу $B_$ можно, так как количество столбцов матрицы $A$ равно количеству строк матрицы $B$. При этом результатом умножения матриц $A_$ и $B_$ будет матрица $C_$, содержащая 5 строк и 9 столбцов:

Заданы матрицы: $ A=\left(\begin -1 & 2 & -3 & 0 \\ 5 & 4 & -2 & 1 \\ -8 & 11 & -10 & -5 \end \right)$ и $ B=\left(\begin -9 & 3 \\ 6 & 20 \\ 7 & 0 \\ 12 & -4 \end \right)$. Найти матрицу $C=A\cdot B$.

Для начала сразу определим размер матрицы $C$. Так как матрица $A$ имеет размер $3\times 4$, а матрица $B$ имеет размер $4\times 2$, то размер матрицы $C$ таков: $3\times 2$:

Итак, в результате произведения матриц $A$ и $B$ мы должны получить матрицу $C$, состоящую из трёх строк и двух столбцов: $ C=\left(\begin c_ & c_ \\ c_ & c_ \\ c_ & c_ \end \right)$. Если обозначения элементов вызывают вопросы, то можно глянуть предыдущую тему: "Матрицы. Виды матриц. Основные термины", в начале которой поясняется обозначение элементов матрицы. Наша цель: найти значения всех элементов матрицы $C$.

Начнем с элемента $c_$. Чтобы получить элемент $c_$ нужно найти сумму произведений элементов первой строки матрицы $A$ и первого столбца матрицы $B$:

Чтобы найти сам элемент $c_$ нужно перемножить элементы первой строки матрицы $A$ на соответствующие элементы первого столбца матрицы $B$, т.е. первый элемент на первый, второй на второй, третий на третий, четвертый на четвертый. Полученные результаты суммируем:

$$ c_=-1\cdot (-9)+2\cdot 6+(-3)\cdot 7 + 0\cdot 12=0. $$

Продолжим решение и найдем $c_$. Для этого придётся перемножить элементы первой строки матрицы $A$ и второго столбца матрицы $B$:

Аналогично предыдущему, имеем:

$$ c_=-1\cdot 3+2\cdot 20+(-3)\cdot 0 + 0\cdot (-4)=37. $$

Все элементы первой строки матрицы $C$ найдены. Переходим ко второй строке, которую начинает элемент $c_$. Чтобы его найти придётся перемножить элементы второй строки матрицы $A$ и первого столбца матрицы $B$:

Следующий элемент $c_$ находим, перемножая элементы второй строки матрицы $A$ на соответствующие элементы второго столбца матрицы $B$:

$$ c_=5\cdot 3+4\cdot 20+(-2)\cdot 0 + 1\cdot (-4)=91. $$

Чтобы найти $c_$ перемножим элементы третьей строки матрицы $A$ на элементы первого столбца матрицы $B$:

$$ c_=-8\cdot (-9)+11\cdot 6+(-10)\cdot 7 + (-5)\cdot 12=8. $$

И, наконец, для нахождения элемента $c_$ придется перемножить элементы третьей строки матрицы $A$ на соответствующие элементы второго столбца матрицы $B$:

$$ c_=-8\cdot 3+11\cdot 20+(-10)\cdot 0 + (-5)\cdot (-4)=216. $$

Все элементы матрицы $C$ найдены, осталось лишь записать, что $C=\left(\begin 0 & 37 \\ -23 & 91 \\ 8 & 216 \end \right)$. Или, если уж писать полностью:

$$ C=A\cdot B =\left(\begin -1 & 2 & -3 & 0 \\ 5 & 4 & -2 & 1 \\ -8 & 11 & -10 & -5 \end \right)\cdot \left(\begin -9 & 3 \\ 6 & 20 \\ 7 & 0 \\ 12 & -4 \end \right)=\left(\begin 0 & 37 \\ -23 & 91 \\ 8 & 216 \end \right). $$

Ответ: $C=\left(\begin 0 & 37 \\ -23 & 91 \\ 8 & 216 \end \right)$.

Кстати сказать, зачастую нет резона расписывать подробно нахождение каждого элемента матрицы-результата. Для матриц, размер которых невелик, можно поступать и так:

$$ \left(\begin 6 & 3 \\ -17 & -2 \end\right)\cdot \left(\begin 4 & 9 \\ -6 & 90 \end \right) =\left(\begin 6\cdot+3\cdot(-6) & 6\cdot+3\cdot \\ -17\cdot+(-2)\cdot(-6) & -17\cdot+(-2)\cdot \end \right) =\left(\begin 6 & 324 \\ -56 & -333 \end \right) $$

Стоит также обратить внимание, что умножение матриц некоммутативно. Это означает, что в общем случае $A\cdot B\neq B\cdot A$. Лишь для некоторых типов матриц, которые именуют перестановочными (или коммутирующими), верно равенство $A\cdot B=B\cdot A$. Именно исходя из некоммутативности умножения, требуется указывать как именно мы домножаем выражение на ту или иную матрицу: справа или слева. Например, фраза "домножим обе части равенства $3E-F=Y$ на матрицу $A$ справа" означает, что требуется получить такое равенство: $(3E-F)\cdot A=Y\cdot A$.

Транспонированная матрица.

Транспонированной по отношению к матрице $A_=(a_)$ называется матрица $A_^=(a_^)$, для элементов которой $a_^=a_$.

Попросту говоря, для того, чтобы получить транспонированную матрицу $A^T$, нужно в исходной матрице $A$ заменить столбцы соответствующими строками по такому принципу: была первая строка – станет первый столбец; была вторая строка – станет второй столбец; была третья строка – станет третий столбец и так далее. Например, найдем транспонированную матрицу к матрице $A_$:

Соответственно, если исходная матрица имела размер $3\times 5$, то транспонированная матрица имеет размер $5\times 3$.

Некоторые свойства операций над матрицами.

Здесь предполагается, что $\alpha$, $\beta$ – некоторые числа, а $A$, $B$, $C$ – матрицы. Для первых четырех свойств я указал названия, остальные можно назвать по аналогии с первыми четырьмя.

1. $A+B=B+A$ (коммутативность сложения)
2. $A+(B+C)=(A+B)+C$ (ассоциативность сложения)
3. $(\alpha+\beta)\cdot A=\alpha A+\beta A$ (дистрибутивность умножения на матрицу относительно сложения чисел)
4. $\alpha\cdot(A+B)=\alpha A+\alpha B$ (дистрибутивность умножения на число относительно сложения матриц)
5. $A(BC)=(AB)C$
6. $(\alpha\beta)A=\alpha(\beta A)$
7. $A\cdot (B+C)=AB+AC$, $(B+C)\cdot A=BA+CA$.
8. $A\cdot E=A$, $E\cdot A=A$, где $E$ – единичная матрица соответствующего порядка.
9. $A\cdot O=O$, $O\cdot A=O$, где $O$ – нулевая матрица соответствующего размера.
10. $\left(A^T \right)^T=A$
11. $(A+B)^T=A^T+B^T$
12. $(AB)^T=B^T\cdot A^T$
13. $\left(\alpha A \right)^T=\alpha A^T$

В следующей части будет рассмотрена операция возведения матрицы в целую неотрицательную степень, а также решены примеры, в которых потребуется выполнение нескольких операций над матрицами.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Линейная алгебра

Определение равенства двух матриц

.

Таким образом, матрицы

равны, если =b_" width="69" height="15" />
, =b_" width="70" height="15" />
, =b_" width="70" height="15" />
, =b_" width="70" height="15" />
, =b_" width="69" height="15" />
, =b_" width="70" height="15" />
, =b_" width="70" height="15" />
, =b_" width="70" height="15" />
, =b_" width="69" height="15" />
, =b_" width="70" height="15" />
, =b_" width="70" height="15" />
, =b_" width="70" height="15" />
, =b_" width="69" height="15" />
, =b_" width="70" height="15" />
, =b_" width="70" height="15" />
, =b_" width="70" height="15" />
.

.

Транспонирование матриц

Если в матрице типа , имеющей вид

переставить строки со столбцами, получим матрицу, типа , которая является транспонированной матрицей:

Если матрица состоит из одной строки (матрица-строка), то при транспонировании такая матрица становится матрицей-столбцом.

Свойства транспонирования матриц

Перечислим свойства транспонирования матриц, немного забежим вперед:

1. Если матрицу транспонировать дважды, то получится исходная матрица.
2. Транспонирование суммы матриц равно сумме транспонированных матриц.
3. Можно умножить исходную матрицу на число или уже транспонированную матрицу умножить на число, порядок умножения не важен. Таким образом, транспонированное произведение матрицы и числа равно произведению этого же числа на транспонированную матрицу.
4. Транспонированное произведение матриц равно произведению транспонированных матриц в обратном порядке

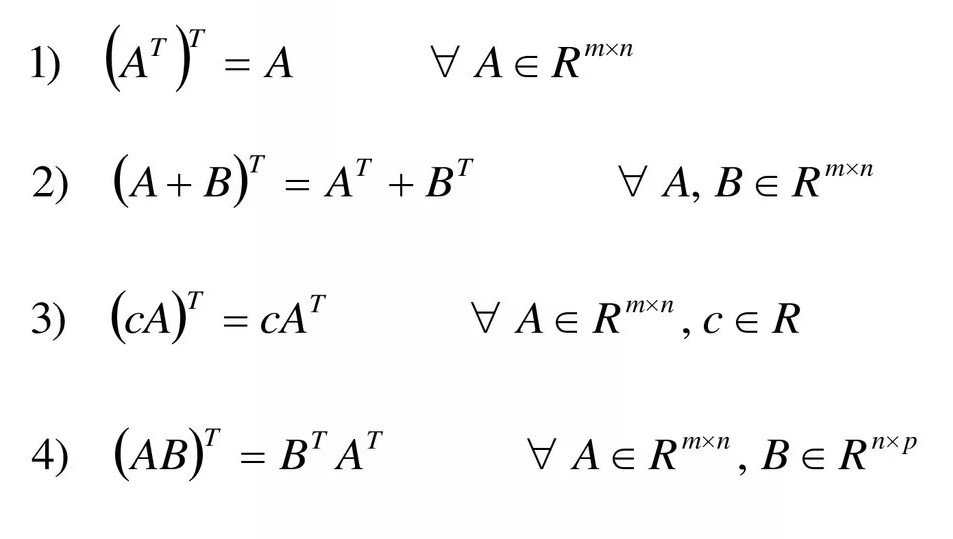
Свойства транспонирования матриц

Транспонирование векторов

При транспонировании векторов матрица-столбец становится матрицей-строкой, а матрица-строка становится матрицей-столбцом. Так, например, матрица-строка

Читайте также:

  
• Как сделать поиск по сайту wordpress
  
• Как сделать нижний регистр в python
  
• Как сделать клатч в дрифте
  
• Как сделать клизму крысе
  
• Как сделать стульчик на турнике