Как сделать сечение в треугольной призме

Добавил пользователь Валентин П.
Обновлено: 31.08.2024

\u0421\u043e\u0435\u0434\u0438\u043d\u0438\u00a0M\u00a0\u0438\u00a0N\u00a0\u0438 \u043f\u0440\u043e\u0434\u043b\u0438 MN \u0434\u043e \u043f\u0435\u0440\u0435\u0441\u0435\u0447\u0435\u043d\u0438\u044f \u0441 AB.\u00a0\u041f\u043e\u0443\u0447\u0438\u0448\u044c\u00a0\u0442\u043e\u0447\u043a\u0443 \u0420.

\u0422\u043e\u0447\u043a\u0443\u00a0\u0420\u00a0\u0441\u043e\u0435\u0434\u0438\u043d\u0438 \u0441 \u0442\u043e\u0447\u043a\u043e\u0439\u00a0\u041a\u00a0:\u00a0[tex]KP\\cap CB=L[\/tex] .
\u0442\u043e\u0447\u043a\u0443\u00a0L\u00a0\u0441\u043e\u0435\u0434\u0438\u043d\u0438 \u0441\u00a0\u0442\u043e\u0447\u043a\u043e\u0439\u00a0N.\u00a0
\u041f\u0440\u043e\u0434\u043b\u0438\u00a0MN\u00a0\u0434\u043e \u043f\u0435\u0440\u0435\u0441\u0435\u0447\u0435\u043d\u0438\u044f \u0441\u00a0[tex]AA1[\/tex] . \u041f\u043e\u043b\u0443\u0447\u0438\u0448\u044c \u0442\u043e\u0447\u043a\u0443 \u0415.

\u0422\u043e\u0447\u043a\u0443\u00a0\u0415\u00a0\u0441\u043e\u0435\u0434\u0438\u043d\u0438 \u0441 \u041a.\u00a0 \u041f\u0440\u044f\u043c\u0430\u044f \u041aE \u043f\u0435\u0440\u0435\u0441\u0435\u0447\u0451\u0442 \u04101\u0421\u00a0\u0432 \u0442\u043e\u0447\u043a\u0435 \u0422:

\u0421\u043e\u0435\u0434\u0438\u043d\u0438 \u0442\u043e\u0447\u043a\u0443 \u0422 \u0438 \u041c. \u041f\u043e\u043b\u0447\u0438\u043c \u0441\u0435\u0447\u0435\u043d\u0438\u0435\u00a0[tex]MNLKT[\/tex] .

в правильной треугольной призме ABCA1B1C1 найдите площадь сечения призмы плоскостью, проходящей через вершины A1 B1 и середину ребра BC
как будет выглядеть сечение ?

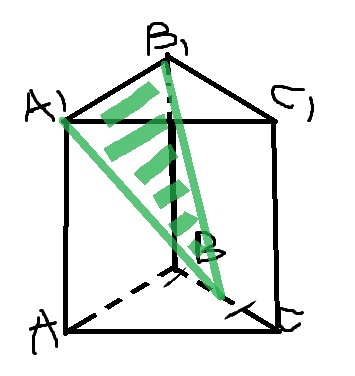
Вот так:

РРР-МЯУ Просветленный (21907) Вот как будет на самом деле.

Пусть середина ВС - точка К, т. е. ВК=КС. Плоскости оснований призмы параллельны друг другу. При пересечении их какой-либо третьей плоскостью, линии ее пересечения с плоскостями обоих оснований будут параллельны друг другу. Поскольку в верхнем основании это А1В1, то в нижнем основании будет линия КМ, параллельная А1В1. А так как АВ параллельна А1В1, то КМ - будет средней линией треугольника АВС. Сечение будет иметь вид равнобедренной трапеции В1КМА1, большее основание В1А1, меньшее основание - КМ, причем КМ=АВ/2=А1В1/2. Чтобы найти площадь сечения, нужно будет вычислять высоту трапеции, для этого недостаточно данных. Нужна либо высота призмы, либо какой -либо угол между элементами плоскости основания и секущей плоскости.
Для облегчения решения "поставьте" призму на еще одну такую же. Тогда трапеция "вырастет" до равнобедренного треугольника А1В1С2 (индексом 2 я обозначил вершины нижнего основания нижней призмы) , и тогда все легко решается.

Призмой зовётся объёмный многогранник, состоящий из двух одинаковых основ – многоугольников, расположенных в перпендикулярных плоскостях. Её боковые грани – прямоугольники или параллелограммы, имеют с ними общие грани. Наклонная призма – геометрическое тело с рёбрами, расположенными к основаниям под углом, отличным от прямого. Её верхняя и нижняя плоскости остаются параллельными.

Разновидности

В основании наклонной призмы может лежать многоугольник с любым количеством рёбер: треугольник, пятиугольник. В зависимости от основания, тело носит соответствующее название, например, квадратная наклонная призма: нижняя и верхняя поверхности – равные квадраты, боковые сформированы параллелепипедами, расположенными к основаниям под отличным от прямого углом.

Полная поверхность – сумма боковых поверхностей, нижней и верхней. Боковая – представлена параллелограммами. Расстояние между плоскостями оснований зовётся высотой геометрического тела.

Наклонная трехгранная или треугольная призма представлена пятигранником с равными основаниями в виде треугольников, которые смещены друг относительно друга. Боковые ребра наклонены к основанию.

Объём вычисляется по классической формуле:

Полная площадь: S = S_бок + 2S_осн или P_оснh + 2S_осн.

Сечения

Сечением тела называется фигура, представленная всеми его точками, расположенными на плоскости a. Перпендикулярное сечение наклонной призмы пересекает её боковые рёбра под углом 90°.

• Перпендикулярные сечения геометрического тела равны один другому.
  
• Сечение будет перпендикулярным боковым ребрам.

Если под углом 90° к боковым граням проходит плоскость сечения, геометрическая фигура называется усечённой. Периметр перпендикулярного сечения такой призмы равен:

• P – периметр фигуры сечения;
  
• l – боковое ребро, например, dD.

Задача

Перпендикулярным сечением наклонной четырехугольной призмы является ромб с диагоналями BD = 24 см, AC = 18 см. Боковая поверхность – 780 см2. Вычислить боковое ребро геометрической фигуры.

Начнём с рассмотрения перпендикулярного сечения. Стороной призмы является высота пересекающей плоскости. Сторона ромба вычисляется благодаря прямоугольному треугольнику AOB, где катеты равны половине диагонали (особенность рассматриваемого многоугольника).

Половины диагоналей OB и AO равны 9 и 12 см.

Воспользуемся теоремой Пифагора:

Дана наклонная призма, в основании которой лежит прямоугольный треугольник. Катеты равны 7 и 24 см. Вершина A₁ находится на одинаковом удалении от вершин треугольника. Вычислить высоту призмы, где ребро AA₁ находится под углом 45° к основанию.

Проекция точки A1 на сторону BC ?АВС представлена точкой O – это центр окружности, описанной вокруг нижнего основания ?АВС. Отсюда следует: O делит гипотенузу ВС на равные отрезки BO = OC. Причём BC ? А₁О – высота геометрического тела.

DА₁ОА является равнобедренным прямоугольным, а отрезки А₁О и АО равны.

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты . Возможно очное и дистанционное обучение по Skype: 1000 р./ак.ч.

6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды

Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.

Грани, пересекаясь, образуют ребра .
Ребра, пересекаясь, образуют вершины .
Рассмотрим два основных вида многогранников:

Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник.

Упражнение

Дана пирамида, основание которой параллельно p₁. Основание представляет собой некоторый треугольник.

S – вершина пирамиды (Рисунок 6.1).

Рисунок 6.1 – Пересечение поверхности пирамиды прямой

Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.

1. Вводим через прямую вспомогательную секущую плоскость s?m и s?p₂.
2. Строим сечение ? (123) поверхности пирамиды с плоскостью s.

Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость s).

Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции необходимо выполнять при помощи пропорционального деления отрезка.

1. В сечении находим точки M и N принадлежащие прямой m.
2. Определяем видимость прямой m.

Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.

Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.

Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.

Основание можно присоединить к любой грани, например, АС (Рисунок 6.2).

Рисунок 6.2 – Построение развёртки пирамиды

В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки \overline,\overline,\overline , проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.

6.2. Призма. Развертка призмы

Призма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях.

Упражнение

Дана призма, основания которой параллельны плоскости проекций p₁.

Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).

1. Вводим через прямую вспомогательную секущую плоскость s?m и s?p₂.
2. Строим сечение поверхности призмы с плоскостью s ->(?(123)).
3. В сечении находим точки K и L принадлежащие прямой m.
4. Определяем видимость прямой m. Если грань АВ на p₂ видна, то точка К на p₂ видима, грань ВС невидима, следовательно, точка Lневидима.

Рассмотрим наклонную призму. Пусть основание призмы параллельно p₁, а ребра параллельны p₂.

Построим нормальное сечение, то есть сечение плоскостью s, перпендикулярной ребрам призмы (Рисунок 6.4).

Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.

Рисунок 6.4 – Построение развёртки призмы
Порядок построения :

1. Найдем истинную величину сечения – (1₀2₀3₀), для чего повернём сечение (123) вокруг оси n?p₂, (можно ввести ДПП p₃//s).
2. Проведём горизонтальную линию на свободном месте листа. Отложим на ней отрезки:
   /1₀-2₀/; /2₀-3₀/; /3₀-1₀/.

1. Проведём направления рёбер перпендикулярно этой линии через точки: 1₀; 2₀; 3₀ и отмерим вверх и вниз расстояния от нормального сечения (на p₂) до верхнего и нижнего основания, откладывая их на линиях-ребрах.

6.3. Взаимное пересечение многогранников

В результате пересечения многогранников получим ломаную линию.

Возможны два случая пересечения многогранников (Рисунок 6.5):

Рисунок 6.5 – Варианты пересечения многогранников

Вершины ломаной – точки пересечения рёбер одного многогранника с гранями другого.

Звенья ломаной – линии пересечения граней.

Для решения задачи нужно найти вершины ломаной, то есть точки пересечения всех рёбер, участвующих в пересечении.

Построенные точки соединить.

Упражнение

Построить линии пересечения призмы с пирамидой (Рисунок 6.6).

Рисунок 6.6. Построение линии пересечения призмы с пирамидой
Решение

1. Находим на p₂ проекции точек пересечения ребра пирамиды с проецирующими гранями призмы (точки 1₂ и 2₂). Находим их горизонтальные проекции.
2. Строим точки пересечения ребра призмы с боковыми гранями пирамиды (точки 3₂ и 4₂), для чего используем вспомогательную плоскость t?p₂.
3. Полученные на p₁ точки 3, 2, 4, 1 соединяем отрезками прямых. Причем отрезки 1₁-3₁, 1₁-2₁, 1₁-4₁ невидимы. Получили замкнутую линию пересечения пирамиды с призмой.

Упражнение

остроить три проекции пирамиды с вырезом и развертку (Рисунок 6.7).

1. По двум проекциям построить третью;
2. На всех трех проекциях построить проекции линии пересечения призматического выреза с пирамидой;
3. Невидимые участки линии пересечения и участки рёбер многогранников показывать штриховой линией;
4. Построить развёртку пирамиды с нанесением линии пересечения.

Рисунок 6.7. Построение проекций пирамиды с вырезом и развертки
Решение :

1. Проводим линии рёбер призмы на всех проекциях.
2. Введём плоскость s?p₂, s//p₁:

• s//АВС – основанию пирамиды;
• s пересекает пирамиду ? сечение подобно DА₁В₁С₁.

Это сечение пересекается:

— с ребром D в двух точках 1 и 4;

— с ребром Е в двух точках 2 и 5.

Соединим найденные точки: 1-2-3-1; 4-6-5-7-4 и определим видимость.

Построение развертки рассмотрено ранее.

6.4. Задачи для самостоятельной работы

1-4. Построить линию пересечения гранных поверхностей. Показать видимость (Рисунки 6.8 – 6.11).

Рисунок 6.8

Рисунок 6.9

Рисунок 6.10

Рисунок 6.11

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты . Возможно очное и дистанционное обучение по Skype: 1000 р./ак.ч.

Читайте также:

  
• Как сделать поворот в трик студио
  
• Как сделать палку
  
• Как сделать панораму в dermandar
  
• Как сделать связку чеснока в sims 4
  
• Как сделать панораму dji mini 2