Как сделать распределение в экселе
В данной статье мы рассмотрим особенности алгоритма генератора случайных чисел в Excel, и на примерах рассмотрим, как использовать функции СЛЧИС и СЛУЧМЕЖДУ в Excel для генерации случайных чисел, случайных чисел с заданным количеством знаков после запятой, дат и времени.
Генератор случайных чисел с использованием функции СЛЧИС
Функция СЛЧИС является одной из двух функций, специально предназначенных для генерации случайных чисел в Excel. Данная функция возвращает случайное десятичное число (действительное число) между 0 и 1.
СЛЧИС() является энергозависимой функцией, что означает, что при каждом вычислении рабочего листа создается новое случайное число. И это происходит каждый раз, когда вы выполняете какое-либо действие на листе, например, обновляете формулу (не обязательно формулу СЛЧИС, любую другую формулу на листе), редактируете ячейку или вводите новые данные.
Функция СЛЧИС доступна во всех версиях: Excel 2016, Excel 2013, Excel 2010, Excel 2007, Excel 2003.
Поскольку функция Excel СЛЧИС не имеет аргументов, вы просто вводите =СЛЧИС() в ячейке и затем копируете формулу на столько ячеек, сколько хотите:

Генератор случайных чисел в Excel – Генерация случайных чисел
А теперь давайте сделаем еще один шаг и напишем несколько формул СЛЧИС для генерации случайных чисел в соответствии с определенными условиями.
Генератор случайных чисел от нуля до заданной верхней границы диапазона
Чтобы сделать генератор случайных чисел от нуля до любого значения N, вы несколько раз выполняете функцию СЛЧИС с помощью N:
Например, для создания последовательности случайных чисел, больших или равных 0, но менее 50, используйте следующую формулу:
Примечание . Значение верхней границы никогда не включается в возвращаемую случайную последовательность. Например, если вы хотите получить случайные числа от 0 до 10, включая 10, правильная формула =СЛЧИС()*11.
Генератор случайных чисел в диапазоне
Чтобы создать случайное число в диапазоне, т.е. случайное число между любыми двумя указанными вами числами, используйте следующую формулу СЛЧИС:
Где A – это нижнее значение границы (наименьшее число), а B – верхнее значение границы (наибольшее число).
Например, чтобы сделать генератор случайных чисел от 10 до 50, вы можете использовать следующую формулу:
Примечание . Эта формула генерации случайных чисел никогда не вернет число, равное наибольшему числу указанного диапазона (значение B).
Генератор случайных целых чисел в Excel
Чтобы функция Excel СЛЧИС создавала случайные целые числа, возьмите одну из вышеупомянутых формул и заверните ее в функцию ЦЕЛОЕ .
Чтобы сделать генератор случайных целых чисел от 0 до 50:
Чтобы генерировать случайные целые числа от 10 до 50:

Генератор случайных чисел в Excel – Генерация случайных целых чисел
Генератор случайных чисел в Excel в диапазоне с помощью функции СЛУЧМЕЖДУ
СЛУЧМЕЖДУ – это еще одна функция в Excel для создания генератора случайных чисел.. Она возвращает случайные целые числа в указанном диапазоне:
СЛУЧМЕЖДУ (нижняя граница; верхняя граница)
Очевидно, что нижняя граница – это наименьшее число, а верхняя граница – наибольшее число в диапазоне случайных чисел, которые вы хотите получить.
Подобно СЛЧИС, СЛУЧМЕЖДУ в Excel является изменчивой функцией, и она также возвращает новое случайное целое число каждый раз, когда ваша таблица пересчитывается или изменяется.
Например, того чтобы сделать генератор случайных целых чисел от 10 до 50 (включая 10 и 50) используйте следующую формулу СЛУЧМЕЖДУ:

Генератор случайных чисел в Excel – Генерация случайных чисел в заданном диапазоне
Функция СЛУЧМЕЖДУ в Excel может создавать как положительные, так и отрицательные числа случайные числа. Например, чтобы получить список случайных чисел от -10 до 10, введите следующую формулу на листе:
Функция СЛУЧМЕЖДУ доступна в следующих версиях: Excel 2016, Excel 2013, Excel 2010 и Excel 2007.
В более ранней версии Excel 2003, вы можете использовать формулу СЛЧИС , рассмотренную выше.
Далее в этой статье вы найдете еще несколько примеров формул, демонстрирующих, как использовать функцию СЛУЧМЕЖДУ для создания генератора случайных чисел, отличных от целых.
Создание случайных чисел с заданным количеством знаков после запятой
Хотя функция СЛУЧМЕЖДУ в Excel была предназначена для генерации случайных целых чисел, вы можете использовать ее для генерации случайных десятичных чисел с таким количеством десятичных знаков, сколько хотите.
Например, чтобы получить список чисел с одним десятичным знаком, вы умножаете нижнее и верхнее значения на 10, а затем делите возвращаемое значение на 10:
= СЛУЧМЕЖДУ(нижняя граница*10; верхняя граница*10)/10
Например, чтобы получить список чисел с одним десятичным знаком, вы умножаете нижнее и верхнее значения на 10, а затем делите возвращаемое значение на 10:
Следующая формула СЛУЧМЕЖДУ возвращает случайные десятичные числа от 1 до 50:

Генератор случайных чисел в Excel – Генерация случайных чисел с одним знаком после запятой
Аналогичным образом, чтобы сделать генератор случайных чисел от 1 до 50 с двумя знаками после запятой, вы умножаете аргументы функции СЛУЧМЕЖДУ на 100, а затем делите результат на 100:

Генератор случайных чисел в Excel – Генерация случайных чисел с двумя знаками после запятой
Генератор случайных дат в Excel
Чтобы вернуть список случайных дат между данными двумя датами, используйте функцию СЛУЧМЕЖДУ в сочетании с ДАТА:
=СЛУЧМЕЖДУ (ДАТА (дата начала); ДАТА (дата окончания))
Например, чтобы получить список дат между 1 сентября 2017 и 20 ноября 2017 включительно, введите следующую формулу на листе:
Не забудьте применить формат даты к ячейке (ячейкам), и вы получите список случайных дат, подобных этому:

Генератор случайных чисел в Excel – Генерация случайных дат
Генератор случайного времени в Excel
Во внутренней системе Excel времена хранятся как десятичные числа, и вы можете использовать стандартную функцию Excel СЛЧИС для вставки случайных действительных чисел, а затем просто применить формат времени к ячейкам:

Генератор случайных чисел в Excel – Генерация случайного времени функцией СЛЧИС и применение к ней формата Время
Чтобы сделать генератор случайного времени в указанном диапазоне, требуется более конкретная формула. Рассмотрим подробнее.
Генератор случайного времени в указанном диапазоне
Чтобы вставить произвольное время между любыми двумя указанными вами временными интервалами, используйте функцию ВРЕМЯ в сочетании с Excel СЛЧИС:
= ВРЕМЯ (время начала) + СЛЧИС () * (ВРЕМЯ (время начала) - ВРЕМЯ (время окончания))
Например, чтобы вставить случайное время между 5:30 и 18:00, вы можете использовать одну из следующих формул:
Генератор случайных чисел в Excel – Генерация случайного времени в заданном интервале
Генератор случайных букв в Excel
Чтобы вставить случайную букву, необходимо использовать комбинацию трех различных функций:
Где A - первый символ, а Z - последний символ в диапазоне букв, которые вы хотите включить (в алфавитном порядке).
Разберем функции, в приведенной выше формуле:
- КОДСИМВ возвращает числовые коды ANSI для указанных букв.
- СЛУЧМЕЖДУ принимает числа, возвращаемые функциями КОДСИМВ , как нижнее и верхнее значения диапазона.
- СИМВОЛ преобразует случайные коды ANSI, возвращаемые СЛУЧМЕЖДУ, в соответствующие буквы.

Генератор случайных чисел в Excel – Генерация случайных букв
Так как коды ANSI отличаются для прописных и строчных букв, эта формула учитывает регистр.
Если кто-то наизусть знает Коды символов ANSI, ничто не мешает вам передавать коды непосредственно в функцию СЛУЧМЕЖДУ.
Например, чтобы получить произвольные прописные буквы между A (код ANSI 65) и Z (код ANSI 90), вы пишете:
Чтобы генерировать строчные буквы между а (код ANSI 97) в z (код ANSI 122), вы используете следующую формулу:

Генератор случайных чисел в Excel – Генерация случайных символов
Как предотвратить повторное вычисление СЛЧИС и СЛУЧМЕЖДУ
Если вы хотите получить постоянный набор случайных чисел, дат или текстовых строк, которые не будут меняться каждый раз, то есть зафиксировать случайные числа, когда лист пересчитывается, используйте один из следующих способов:

Генератор случайных чисел в Excel – Вставка значений
Генератор случайных чисел с помощью Анализа данных
С помощью пакета анализа данных вы, например, можете сгенерировать случайные числа нормального распределения или другого распределения. По умолчанию данный пакет не подключен, поэтому необходимо его загрузить. Как это сделать, описано в этой статье.
Пример генерации случайных чисел нормального распределения

Генератор случайных чисел в Excel – Анализ данных

Генератор случайных чисел в Excel – Генерация случайных чисел

Генератор случайных чисел в Excel – Генерация случайных чисел нормального распределения
Ну вот на этом все. Теперь вы научились, как сделать генератор случайных чисел, чисел в диапазоне, чисел с заданным количеством знаков после запятой, случайных дат, случайного времени, а также случайных букв, а также, как сгенерировать случайные числа нормального распределения. Таким образом, владея данными знаниями, вы можете создать не только генератор случайных чисел в Excel, но и генератор паролей.
При изучении величины, принимающей случайные значения (результатов физических измерений в серии экспериментов, экономических показателей, параметров технологических процессов и т.п.), мы имеем дело с выборками. Выборочное наблюдение – это способ наблюдения, при котором обследуется не вся совокупность значений изучаемой величины, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.
При выборочном наблюдении обследованию подвергается определенная, заранее обусловленная часть совокупности, а результаты обследования распространяются на всю совокупность.
Ту часть единиц, которая отобрана для наблюдения, принято называть выборочной совокупностью или выборкой, а всю совокупность единиц, из которых производится отбор, – генеральной совокупностью.
Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности п.
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).
Элементами выборки (x1 х2, . хп) являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (а, b).
Вариационный ряд получается из выборки упорядочением по возрастанию (или убыванию) и подсчетом частоты каждого значения. Если вариационный ряд содержит значения признака и соответствующие ему частоты,то такой ряд носит название дискретный вариационный ряд. Если нам известно, что исследуемый показатель может принимать любые значения из некоторого интервала, то строим интервальный вариационный.
Удобнее всего ряды распределения анализировать с помощью их графического изображения, позволяющего судить о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.
Пример 2.1.
Известны следующие данные о результатах сдачи студентами экзамена (в баллах):
| 18 | 16 | 20 | 17 | 19 | 20 | 17 |
| 17 | 12 | 15 | 20 | 18 | 19 | 18 |
| 18 | 16 | 18 | 14 | 14 | 17 | 19 |
| 16 | 14 | 19 | 12 | 15 | 16 | 20 |
Необходимо построить ряд распределения числа студентов по баллу, представить графически результаты.
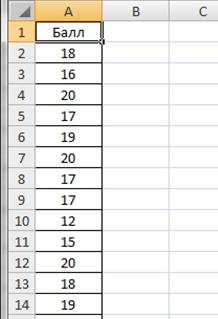
Рисунок 2.6. Баллы успеваемости студентов
Определим наименьший и наибольший балл по выборке. Для этого введем в ячейках С1 и С2 соответственно введем формулы =МИН(A2:A29) и =МАКС(A2:A29). Получим значения 12 и 20 соответственно (рис.2.7).
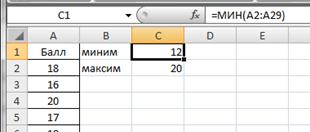
Рисунок 2.7. Минимальный и максимальный балл
Построим вариационный ряд. Для каждого значения необходимо подсчитать частоту. Так как значения признака (балл) отличаются на единицу, то можно воспользоваться следующим способом. В ячейку С4 введем формулу =С1, в С5 соответственно С4+1. Ячейку С5 протянем маркером заполнения (правый нижний угол ячейки) вниз до С12. Результаты представлены на рисунке 2.8.
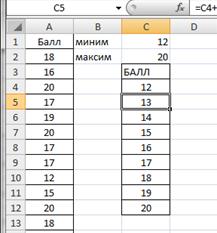
Рисунок 2.8. Значения признака
Вычислим частоту для каждого значения признака. В ячейку D4 введем формулу =СЧЕТЕСЛИ(A$2:A$29;C4) и протянем D4 маркером вниз до заполнения D12. В ячейке D13 просуммируем частоты с помощью формулы =СУММ(D4:D12).
Получим вариационный ряд (значения признака и соответствующие им частоты) на рисунке 2.9.
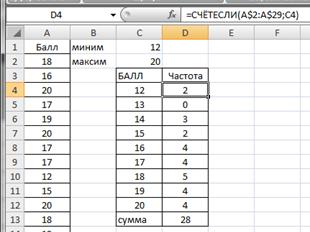
Рис.2.9. Частоты вариационного ряда
Вычислим частость (относительную частоту) для каждого значения признака. В ячейку Е4 введем формулу = D4/D$13. Протянем Е4 маркером заполнения вниз до Е12 (рис.2.10).
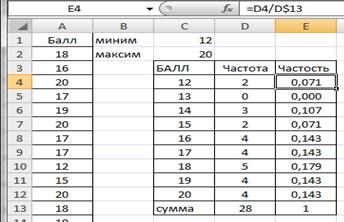
Рисунок 2.10. Частости ряда распределения
Вычислим накопленные частоты. В ячейку F4 введем формулу =D4, а в ячейку F5 – формулу = D5+F4. Протянем F5 маркером заполнения вниз до F12 (рис.2.11).
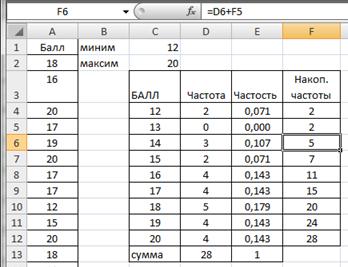
Рисунок 2.11. Накопленные частоты ряда
Построим эмпирическую функцию распределения, т.е. найдем наколенные частости. Выделим F4:F12 и маркером заполнения протянем вправо на соседний столбец (рис.2.12). В G4 получим формулу = Е4, в ячейке G5 формулу =Е5+ G4 и т.д.
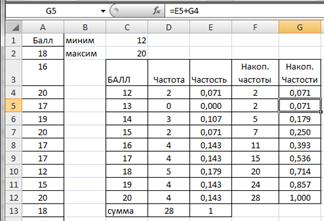
Рисунок 2.12. Накопленные частости ряда
Рисунок 2.13. Полигон распределения частот
Рисунок 2.14. Полигон распределения частостей
Рисунок 2.15. Гистограмма распределения частостей
Рисунок 2.16. Кумулята
Пример 2.2.
В таблице 2.7 представлены значения процентных ставок по кредитам по 30 коммерческим банкам.
Банковские процентные ставки
| № Банка | Процентная ставка, % |
| 1 | 20,3 |
| 2 | 17,1 |
| 3 | 14,2 |
| 4 | 11,0 |
| 5 | 17,3 |
| 6 | 19,6 |
| 7 | 20,5 |
| 8 | 23,6 |
| 9 | 14,6 |
| 10 | 17,5 |
| 11 | 20,8 |
| 12 | 13,6 |
| 13 | 24,0 |
| 14 | 17,5 |
| 15 | 15,0 |
| 16 | 21,1 |
| 17 | 17,6 |
| 18 | 15,8 |
| 19 | 18,8 |
| 20 | 22,4 |
| 21 | 16,1 |
| 22 | 17,9 |
| 23 | 21,7 |
| 24 | 18,0 |
| 25 | 16,4 |
| 26 | 26,0 |
| 27 | 18,4 |
| 28 | 16,7 |
| 29 | 12,2 |
| 30 | 13,9 |
Построим интервальный вариационный ряд. Для этого вычислим границы интервалов (карманов) с использованием формулы Стэрджесса.
Введем данные в диапазоне A1:A31 (рис.2.17). Определим максимальное и минимальное значения (ячейки С2 и С3 соответственно) так же как и в примере 2.1. Определим число интервалов по формуле Стэрджесса, для чего в ячейку С6 введем формулу =ЦЕЛОЕ(1+3,322*LOG10(30)) (рис.2.18).
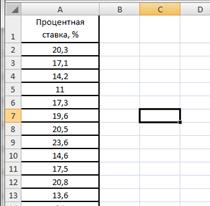
Рисунок 2.17. Процентные ставки банков

Рисунок 2.18. Число интервалов
Вычислим длину интервалов, для чего в ячейке С8 введем формулу =ОКРУГЛ((C3-C2)/C6;2) (рис.2.19).
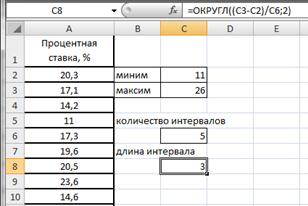
Рисунок 2.19. Длина интервала
Определим нижние и верхние границы интервалов (карманы), для чего в ячейке Е2 запишем формулу =С2, в ячейке Е3 запишем ==E2+$C$8. Протянем Е3 маркером заполнения вниз до Е7 (рис.2.20).
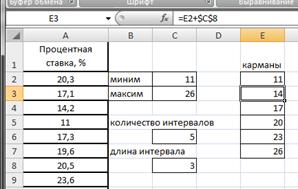
Рисунок 2.20. Границы интервалов
Подсчитаем частоты – в интервал считаем те значения, которые больше нижней границы интервала или равны ей и меньше верхней границы.
Воспользуемся функцией ЧАСТОТА. Для этого в ячейке F2 введем формулу =ЧАСТОТА(A2:A31;E2:E7). Протянем F2 маркером заполнения вниз до F8.
Формулу в этом примере необходимо ввести как формулу массива. Выделим диапазон F2:F8, нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ВВОД (рис.2.21).
Если формула не будет введена как формула массива, отобразится только одно ее значение в ячейке F2.
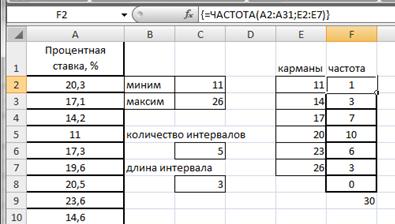
Рисунок 2.21. Частоты значений признака
Также можно воспользоваться средством Пакета анализа (Анализ данных в Office 2007) ГИСТОГРАММА (рис.2.22). Выберем входной интервал, интервал карманов, метки, интегральный процент, поместим результаты на этом же листе (укажем ячейку $H$2).
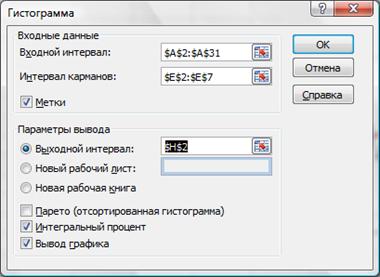
Рисунок 2.22. Построение гистограммы
Полученная гистограмма представлена на рис.2.23.
Рис.2.23. Гистограмма частот
Замечание. Если диапазон карманов не был введен, то набор отрезков, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.
Вариационный ряд может быть:
– дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.

Построить вариационный ряд и полигон распределения
Решение .
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel

5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда

Построим полигон:
Рис.1.3. Пример 1. Построение полигона частот
В реальных социально-экономических системах нельзя проводить активные эксперименты, поэтому данные обычно представляют собой наблюдения за происходящим процессом, например: курс валюты на бирже в течение месяца, урожайность пшеницы в хозяйстве за 30 лет, производительность труда рабочих за смену и т.д. Результаты наблюдений — это в общем случае ряд чисел, расположенных в беспорядке, который для изучения необходимо упорядочить (проранжи- ровать).
Операция, заключающаяся в расположении значений признака по возрастанию, называется ранжированием опытных данных.
После операции ранжирования опытные данные можно сгруппировать так, чтобы в каждой группе признак принимал одно и то же значение, которое называется вариантом (х,). Число элементов в каждой группе называется частотой варианта («,).
Размахом вариации называется число

где хтах — наибольший вариант;
x min — наименьший вариант.
Сумма всех частот равна определенному числу л, которое называется объемом совокупности:

Отношение частоты данного варианта к объему совокупности называется относительной частотой, или частостью, этого варианта:

Последовательность вариант, расположенных в возрастающем порядке, называется вариационным рядом (вариация — изменение).
Вариационные ряды бывают дискретными и непрерывными. Дискретным вариационным рядом называется ранжированная последовательность вариант с соответствующими частотами и (или) частостями.
Пример 1. В результате тестирования группа из 24 человек набрала баллы: 4, 0, 3, 4, 1, 0, 3, 1, 0, 4, 0, 0, 3, 1, 0, 1, 1, 3, 2, 3, 1, 2, 1, 2. Построить дискретный вариационный ряд.
Решение. Проранжируем исходный ряд, подсчитаем частоту и частость вариант: 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4.
В результате получим дискретный вариационный ряд (табл. 3.10).
Ранжированный ряд успеваемости
Число студентов, л,
Относительная частота, А
В Excel проранжируем исходный ряд. Для этого введем все данные в диапазон А1 :А24 и воспользуемся кнопкой Щ (Сортировка по возрастанию).
Подсчитаем частоту и частость вариант. Построим таблицу в диапазоне D2:G7 (рис. 3.13).

Рис. 3.13. Контекстное меню строки состояния
Рассмотрим два варианта подсчета частот:
- 1) выделим диапазон, в котором находятся нули. Щелкнем в нижней правой части окна Excel правой кнопкой мыши и выберем в контекстном меню вид итога, который по умолчанию будет появляться в итоговой строке при выделении произвольного диапазона (см. рис. 3.13) — количество. Таким образом, последовательно выделяя диапазоны с одинаковыми значениями вариант, мы получим все частоты;
- 2) выполним команду Сервис — Анализ данных — Гистограмма. Заполним диалоговое окно в соответствии с рис. 3.14.

В результате получим таблицу с частотами вариантов и соответствующий график (рис. 3.15).

Рис. 3.15. Результаты применения инструмента «Гистограмма)
Найдем объем выборки, заполнив все частоты вариант в диапазоне ЕЗ:Е7, выделим его левой кнопкой мыши и щелкнем по кнопке ? (автосумма).
Excel – это эффективный инструмент для статистической обработки данных. И определение корреляций является очень важной составляющей этого процесса. Программа имеет весь необходимый инструментарий для осуществления расчетов такого плана. Сегодня мы более детально разберемся, что нам нужно для осуществления анализа этого типа.
Что представляет собой корреляционный анализ
Простыми словами, корреляция – это связь между двумя явлениями. В свою очередь, под корреляционным анализом подразумевают выявление этой связи. Очень частое утверждение гласит, что корреляция – это зависимость между разными объектами, но на деле это неточное определение. Ведь существует множество изображений, которые показывают связь между явлениями, которые никак не могут быть зависимы друг от друга или одного третьего фактора, который влияет на них.
Для определения зависимости используется другой тип анализа, который называется регрессионным.
Величина, определяющая степень выраженности взаимосвязи, называется коэффициентом корреляции. Это единственная величина, которая рассчитывается корреляционным анализом по сравнению с регрессионным. Возможные вариации коэффициента корреляции могут быть в пределах от -1 до 1. Если это число положительное, взаимосвязь между динамикой изменения значений прямая. Если же отрицательное, то увеличение числа 1 приводит к аналогичному уменьшению числа 2. Если число меньше единицы по модулю, то корреляция неполная. Например, увеличение числа 1 на единицу приводит к увеличению числа 2 на 0,5. В таком случае коэффициент корреляции составляет 0,5. Если же коэффициент корреляции составляет 0, то взаимосвязи между двумя переменными нет.
Интересный факт: корреляции делятся на истинные и ложные. То есть, иногда то, что графики идут в одинаковом направлении, может быть чистой случайностью, а не закономерным следствием воздействия одной переменной на другую или влияния общего фактора на обе переменные. В узких кругах довольно популярны картинки, где коррелируют между собой абсолютно не связанные явления. Вот некоторые примеры:
Ну и наконец, еще один пример ложной корреляции – чем больше сыра люди едят, тем больше людей умирает из-за того, что они запутываются в своих простынях.
Поэтому несмотря на то, что корреляция является эффективным статистическим инструментом, нужно учиться отфильтровывать истинные взаимосвязи между явлениями и ложные. Иначе исследование может получить такие интересные результаты. А теперь переходим непосредственно к тому, как проводить корреляционный анализ в Excel.
Корреляционный анализ в Excel — 2 способа
Вычисление коэффициента корреляции осуществляется двумя способами. Первый – это использование Мастера функций, который позволяет ввести формулу КОРРЕЛ. Второй инструмент – это пакет анализа, требующий отдельной активации.
Как рассчитать коэффициент корреляции
Давайте продемонстрируем механизм получения коэффициента корреляции на реальном кейсе. Допустим, у нас есть таблица с информацией о суммах продаж и рекламу. Нам нужно понять, в какой степени количество продаж и количество денег, которые были использованы на продвижение, взаимосвязаны.
Способ 1. Определение корреляции с помощью Мастера Функций
Функция КОРРЕЛ – один из самых простых методов, как можно реализовать поставленную задачу. В своем общем виде этот оператор имеет следующий вид: КОРРЕЛ(массив1;массив2). Как же ее ввести? Для этого нужно осуществлять следующие действия:

После выполнения описанных выше шагов мы видим в ячейке, выбранной нами на первом этапе, коэффициент корреляции. В нашем примере он составляет 0,97, что указывает на очень сильно выраженную взаимосвязь между данными двух диапазонов.
Способ 2. Вычисление корреляции с помощью пакета анализа
Также довольно неплохой инструмент для определения корреляции между двумя диапазонами – пакет анализа. Но перед тем, как его использовать, нам надо его включить. Для этого выполняем следующие действия:


Поскольку мы оставили поле с данными о том, куда будут выводиться результаты, таким, каким оно было, мы переходим на новый лист. На нем можно найти коэффициент корреляции. Конечно, он такой же самый, как был в предыдущем методе – 0,97. Причина этого в том, что вычисления производятся одинаковые, исходные данные мы также не меняли. Просто разными методами, но не более.
Таким образом, Эксель дает сразу два метода осуществления корреляционного анализа. Как вы уже понимаете, в результате вычислений итог получится таким же. Но каждый пользователь может выбрать тот метод расчета, который ему больше всего подходит.
Как построить поле корреляции в Excel

Итак, давайте теперь разберемся, как построить поле корреляции. Для начала нужно разобраться, что это вообще такое. Под корреляционным полем подразумевается фактически график корреляции. Главное требование к такой диаграмме – каждая точка должна соответствовать единице совокупности. Поле корреляции поможет установить более глубокие связи и проанализировать данные более качественно. Для начала нам нужно найти коэффициент корреляции между двумя диапазонами, используя функцию КОРРЕЛ.
После того, как мы это сделали, мы теперь можем сделать поле корреляции. Для этого выполняем следующие действия:
Этот график можно построить не только на основе корреляции, определенной через функцию КОРРЕЛ.
Диаграмма рассеивания. Поле корреляции
До сих пор часть пользователей сидит на старой версии Word. Как построить корреляционное поле в этом случае? Для этого существует специальный инструмент, который называется мастером диаграмм. Найти его можно на панели инструментов по специфическому изображению диаграммы. Если навести на эту иконку мышкой, то появится всплывающая подсказка, которая поможет нам убедиться в том, что это действительно мастер диаграмм.
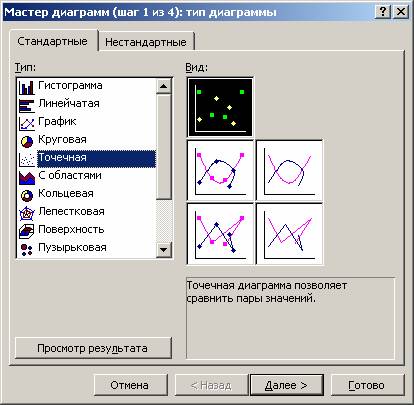
После подтверждения действий у нас появится что-то типа такого графика.
Как видим, возможных вариантов построения может быть огромное количество.
1. Определить выборочные оценки числовых характеристик случайной величины.
Для нахождения выборочных оценок скопируем данные задачи в один столбец таблицы MS Excel . Выделите полученный столбец и на панели инструментов щелкните на кнопку Сортировка и фильтр . В появившемся окошке нажмите сортировку от А до Я. В выделенном столбце значения упорядочатся от наименьшего к наибольшему.
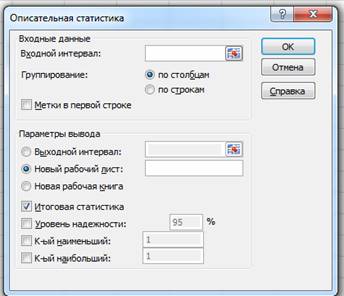
Проанализируем данные с помощью описательной статистики. Для этого на вкладке Данные в группе Анализ щелкните на кнопку Анализ данных . Откроется диалоговое окно Анализ данных.
Выберите инструмент Описательная статистика и щелкните на кнопке Ок . Откроется диалоговое окно Описательная статистика.
2. Построить вариационный ряд, или ряд распределений и гистограмму для него.
Как видно в итоговой статистике, все возможные значения данного распределения укладываются в интервал 3s.
Действительно, x =69,43; 3s=27,3; ( x -3s; x +3s) = (41,13; 96,73)
Размах выборки 43,6. Разбиваем данный ряд на 7 интервалов длины 43,6: 7?6,2.
Составим таблицу ряда распределений:
Чтобы создать диаграмму, выберите нужные данные таблицы (границы интервала и число наблюдений в интервале) и на вкладке Вставка в группе Диаграммы щелкните на типе диаграммы. Появится список доступных подтипов диаграмм. При щелчке на подтипе диаграммы будет создана диаграмма с макетом и цветовой схемой по умолчанию, определенными в теме оформления книги.
3. Определить теоретическую функцию распределения, её параметры. Выполнить сравнительный графический анализ формы эмпирического и теоретического распределений.
Для построения графика теоретической функции распределения построим вспомогательную таблицу:
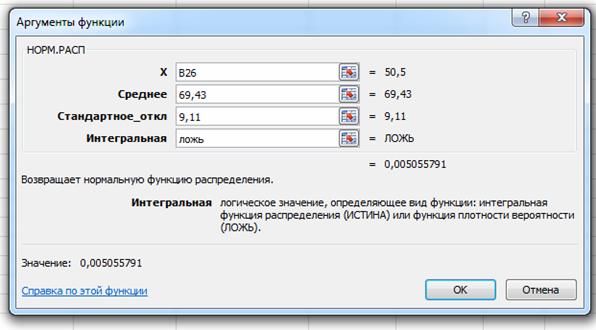
В открывшемся окне в поле X указываем на ячейку со значением середины интервала, в поле Среднее указываем среднее значение, полученное в первом пункте работы с помощью описательной статистики, в поле Стандартное_откл – стандартное отклонение, найденное также с помощью описательной статистики. В поле Интегральная – ЛОЖЬ, так как ищем функцию плотности вероятности и нажимаем ОК.
Теоретическая вероятность вычисляется по формуле:
В таблице 2 выделяем последний столбец и строим график теоретической вероятности. Для этого на вкладке Вставка в группе График щелкните на типе графика. Появится список доступных подтипов графиков. При щелчке на подтипе графика будет создан график с макетом и цветовой схемой по умолчанию, определенными в теме оформления книги.
Изначально на горизонтальной оси обозначены номера интервалов. Правой кнопкой мыши щелкаем на эту ось и нажимаем на Выбрать данные . Меняем подпись горизонтальной оси, указывая первый столбец таблицы 2. Нажимая на график правой кнопкой мыши можно поменять цвет графика.
А теперь выполним сравнительный графический анализ формы эмпирического и теоретического распределений построением графика теоретической вероятности на гистограмме частот.
Для этого построим гистограмму частостей на интервалах. Щелкнем правой кнопкой мыши в поле гистограммы и нажмем на кнопку Выбрать данные . В открывшемся окне в левом столбце Элементы легенды нажмем кнопку Добавить . Откроется окно Изменение ряда . Имя ряда: укажем на ячейку Теоретическая вероятность, значения: выделим соответствующую строку. После нажатия Ок появится гистограмма теоретических вероятностей. Укажем на неё правой кнопкой мыши и выберем Изменить тип диаграммы для ряда, выбрав график. Также поменяем цвет нового графика.
4.Проверка согласованности теоретического и эмпирического распределений.
Схема применения критерия CH 2 для проверки гипотезы H0 о соответствии эмпирического ряда нормальному закону распределения, сводится к следующему.
1) Определяется мера расхождения эмпирических и теоретических частот CH 2 по формуле .
Для этого в свободной ячейке нажмем на вкладке Формулы выберем Статистические и, среди них ХИ2.ТЕСТ. Откроется следующее окно:
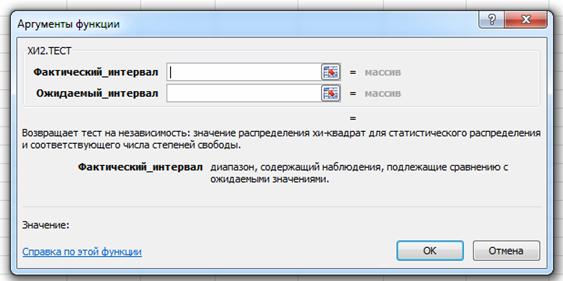
В строке Фактический интервал укажем столбец с частостями из таблицы1. В строке Ожидаемый интервал укажем столбец с теоретическими вероятностями из таблицы2. Нажимая на кнопку Ок, получим наблюдаемое значение CH 2 .
2) Для выбранного уровня значимости a находим критическое значение CH 2 при числе свободы k-r-1 (в нашем случае для нормального распределения k-3).
Для этого в свободной ячейке нажмем на вкладке Формулы кнопку Другие функции и выбираем Статистические .Среди них ? ХИ2.ОБР.ПХ (так как находим правостороннюю критическую область распределения хи-квадрат). Откроется следующее окно:

Встречаются только в пределах полного разврата, лучшие путаны Богородицк, фото свои, не типаж - redbogorodick.ru. Если говорить конкретно, то с проститутками можно заняться не только классическим сексом, но и всем, чем пожелаете. Милые лучшие путаны Богородицк, горячие и прелестные, они такие модельные и молоденькие, что удовольствие неизбежно. Прелестницы ждут тебя.
Читайте также:
