Обновлено: 11.10.2024

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel для iPad Excel Web App Excel для iPhone Excel для планшетов с Android Excel 2010 Excel 2007 Excel для Mac 2011 Excel для телефонов с Android Excel для Windows Phone 10 Excel Mobile Excel Starter 2010 Больше. Основные параметры

Есть несколько способов исправления этой ошибки.

Убедитесь в том, что делитель в функции или формуле не равен нулю и соответствующая ячейка не пуста.

Измените ссылку в формуле, чтобы она указывала на ячейку, не содержащую ноль (0) или пустое значение.

Оценка знаменателя на наличие нуля или пустого значения

Эту ошибку также можно скрыть, вложенную операцию деления в функцию ЕСЛИERROR. При использовании A2/A3 можно использовать =ЕСЛИERROR(A2/A3;0). Эта формула Excel, если формула возвращает ошибку, возвращает 0, в противном случае возвращает результат формулы.

В версиях до Excel 2007 можно использовать синтаксис ЕСЛИ(ЕОШИБКА()): =ЕСЛИ(ЕОШИБКА(A2/A3);0;A2/A3) (см. статью Функции Е).

Совет: Если в Microsoft Excel включена проверка ошибок, нажмите кнопку рядом с ячейкой, в которой показана ошибка. Выберите пункт Показать этапы вычисления, если он отобразится, а затем выберите подходящее решение.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Мы все знаем, 0/0 есть Undefined и возвращает ошибку, если бы я поместил ее в калькулятор, и если бы я создал программу (по крайней мере, на C), ОС прервала бы ее, когда я попытался бы разделить на ноль.

Для пояснения терминологии здесь 0/0 называется неопределенной формой, а x / 0 для ненулевого x не определено . Вычисление, которое заканчивается 0/0, часто может быть рассчитано по-другому, чтобы дать реальный ответ, тогда как x / 0 по сути бессмысленно.

@jwg тогда тебя может заинтересовать правило l'hopital. Определенно есть случаи, когда 0/0 не подразумевает значение 1.

Процессор имеет встроенное обнаружение. Большинство архитектур наборов команд указывают, что ЦП будет перехватывать обработчик исключений для целочисленного деления на ноль (я не думаю, что все равно, будет ли делиться ноль).

Вполне возможно, что проверка делителя нуля происходит параллельно в аппаратном обеспечении вместе с попыткой выполнить деление, однако обнаружение нарушающего условия фактически отменяет деление и прерывает ловушку, поэтому мы не можем действительно сказать, является ли какая-то часть из этого попытался разделение или нет.

(Аппаратное обеспечение часто работает таким образом, выполняя несколько операций параллельно, а затем выбирая соответствующий результат, потому что тогда каждая из операций может быть начата сразу же, вместо того, чтобы сериализовать выбор соответствующей операции.)

Тот же механизм прерывания и исключения будет также использоваться при включении обнаружения переполнения, которое вы обычно запрашиваете, используя различные инструкции add / sub / mul (или флаг этих инструкций).

Деление с плавающей запятой также имеет встроенное обнаружение деления на ноль, но возвращает другое значение ( IEEE 754 указывает NaN ) вместо перехвата в обработчик исключений.

Гипотетически говоря, если процессор пропустил какое-либо обнаружение для попытки деления на ноль, проблемы могут включать:

• зависание ЦП (например, в цикле инф.) - это может произойти, если ЦП использует алгоритм деления, который останавливается, когда числитель меньше делителя (в абсолютном значении). Зависание, подобное этому, в значительной степени будет рассматриваться как сбой процессора.
• (возможно, предсказуемый) мусорный ответ, если ЦП использует счетчик для завершения деления на максимально возможном количестве шагов деления (например, 31 или 32 на 32-битной машине).

@Ankush В случае, если то, что сказал lxrec, было неясно: что касается процессора, то такой вещи, как сбой, не существует.

Это зависит от языка, от компилятора, от того, используете ли вы целые числа или числа с плавающей запятой и так далее.

Для числа с плавающей запятой большинство реализаций используют стандарт IEEE 754 , где деление на 0 четко определено. 0/0 дает четко определенный результат NaN (не число), а x / 0 для x ? 0 дает либо + Infinity, либо -Infinity, в зависимости от знака x.

В таких языках, как C, C ++ и т. Д. Деление на ноль вызывает неопределенное поведение. Таким образом, согласно определению языка, все может произойти. Особенно то, чего ты не хочешь. Как и все отлично работает, когда вы пишете код и уничтожаете данные, когда его использует ваш клиент. Так что с языковой точки зрения не делайте этого . Некоторые языки гарантируют, что ваше приложение потерпит крах; это зависит от них, как это реализовано. Для этих языков деление на ноль приведет к сбою.

Чтобы добавить комментарий @ MichaelKj?rling: в ОС есть способы уведомления об этом (и других видах ошибок). В мире окон это EXCEPTION_INT_DIVIDE_BY_ZERO значение в EXCEPTION_RECORD котором будет обрабатываться (надеюсь) установлен изготовленном Exception Handling Handler

Иногда они делают что-то, кроме гарантии того, что ваше приложение будет аварийно завершено. Например, многие языки / платформы гарантируют, что они сгенерируют исключение при делении на ноль. Затем вы можете поймать и обработать указанное исключение без сбоев.

Похоже, вам интересно, что произойдет, если кто-то создаст процессор, который явно не проверяет ноль перед делением. Что произойдет, полностью зависит от осуществления деления. Не вдаваясь в подробности, один вид реализации даст результат, в котором установлены все биты, например 65535 на 16-битном процессоре. Другой может повесить трубку.

Поскольку x/0 бессмысленно, точка зрения, компьютеры всегда должны проверять деление на ноль. Здесь есть проблема: программисты хотят вычислять (a+b)/c без необходимости проверять, имеет ли этот расчет смысл. Внутренний ответ на деление на ноль ЦП + тип числа + операционная система + язык заключается в том, чтобы либо сделать что-то довольно радикальное (например, аварийно завершить программу), либо сделать что-то слишком мягкое (например, создать значение, которое не смысл, такой как IEEE с плавающей точкой NaN , число, которое "не число").

В обычных условиях программист должен знать, (a+b)/c имеет ли смысл. В этом контексте нет причин проверять деление на ноль. Если происходит деление на ноль, и если машинный язык + язык реализации + тип данных + ответ операционной системы на это должен привести к аварийному завершению программы, это нормально. Если ответ заключается в создании значения, которое в конечном итоге может загрязнить каждое число в программе, это тоже нормально.

То, что NaN не подчиняется арифметике, которую вы изучали в школе, не означает, что в этом нет смысла. Это подчиняется другой арифметике

В современной системе вычисление передается в MPU внутри CPU и помечается как недопустимая операция, возвращаясь NaN .

В гораздо более старых системах, таких как домашние компьютеры 80-х годов, у которых не было деления на кристалле, расчеты выполнялись любым программным обеспечением. Есть несколько возможных вариантов:

• Вычитайте все меньшие и меньшие копии делителя, пока значение не достигнет нуля, и проследите, какие копии размера были вычтены
  • Если он проверяет ноль перед первым вычитанием, он быстро завершится и результат будет 0
  • Если предполагается, что он должен быть в состоянии вычесть хотя бы один раз, результат будет 1
  • При попытке расчета может произойти переполнение, log(0) и программа либо использует свои процедуры обработки ошибок, либо вылетает
  • Программное обеспечение может предполагать, что все логарифмы могут быть рассчитаны с фиксированным числом шагов и возвращать большое, но неправильное значение. Поскольку оба логарифма будут одинаковыми, разница будет 0 и e 0 = 1, что дает результат 1

  Другими словами, то, что произойдет, будет зависеть от реализации, и можно будет написать программное обеспечение, которое будет давать правильные и предсказуемые результаты для каждого значения, но, казалось бы, странные значения для 0/0 этого, тем не менее, все еще внутренне согласованы.

  Этот вопрос касается деления на ноль в целых числах, а в целых числах такого понятия не существует NaN .

  Никакой процессор не собирается вычислять журналы и вычитать, чтобы вычислить результат деления. Время команды логарифма на несколько порядков больше, чем деление. Каково значение log (0)?

  @DavidHammen ОП ни разу не упомянул целые числа, и никто из них не прокомментировал этот вопрос. Целые числа упоминаются только в ответах.

  @wallyk Я уже сказал в своем ответе, что логарифмы very inefficient для деления. Стоимость арифметики (сложение = вычитание)

  Запрос в 1с и деление на ноль

  
  

  
  

  В принципе ето лечится проверкой на ноль с помощю констукции:

  Эту конструкцию можно использовать как в запросе:

  
  

  Так и на закладке с вычисляемыми полями

  
  

  Результат будет одинаковый.

  
  

  
  

  Учителя многое недоговаривали

  Но может ли учитель объяснить маленькому ребенку, что такое принцип неопределенности или натуральный предел? Куда проще будет сказать, что на 0 делить нельзя. Правило не является совсем правдивым, зато школьник не будет пытаться решить уравнение, которое имеет несколько миллиардов решений. Если же в процессе разбора задачи выходит так, что все-таки приходится поделить на ноль, значит, где-то была допущена ошибка.

  На самом деле у такой задачи может быть и иное решение — бесконечность (при условии, что при расчетах не было допущено ошибок). Чтобы это доказать, не придется использовать формулу массы или закон сохранения энергии из физики. В

  большинстве случаев алгебраическое доказательство сводится к решению одного простого уравнения или функции, которая в итоге имеет бесконечное количество решений.

  Четыре действия в арифметике

  Сложение, умножение, деление и вычитание — эти принципы известны каждому школьнику, учащемуся в средних классах. Однако далеко не все знают, что равноправными действиями обладают лишь первые два из них.

  
  

  Деление и вычитание — это операции, которые являются обратными сложению и умножению. Любые действия в математике могут быть легко построены лишь с помощью этих двух основ. Нужно лишь знать, как правильно выражать деление с помощью умножения или вычитание с помощью сложения. Здесь на помощь приходят уравнения, а также положительные и отрицательные числа. Иногда также приходится возводить число в какую-нибудь степень.

  
  

  Принцип бесконечности

  
  

  Арифметическая шутка с нулем

  
  

  Философия, да и только

  
  

  То же самое и с делением на бесконечность. Да, мы можем записать огромное количество решений для функций и уравнений, в которых приходится делить на ноль. Но что в итоге это даст? Бесконечность — число или понятие, которое находится за гранью нашего восприятия. Решение подобного уравнения сравнимо с путешествием в кроличью нору. Даже если конечный результат не будет достигнут — есть над чем задуматься. К примеру, насколько же все-таки многогранным и удивительным является это число — ноль. Оно одновременно ничего не значит и значит слишком много.

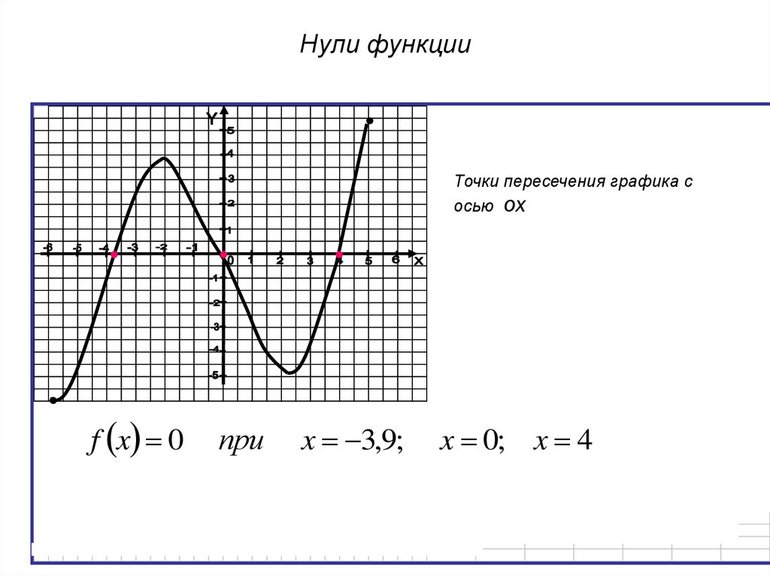
  График функции с нулем

  
  

  Лучше всего понять, что тип уравнения, в котором приходится делить на ноль, имеет бесконечное количество решений, помогает обычный график функции, который доводилось изучать каждому школьнику. Если говорить точнее, то потребуется гипербола, которая имеет обратную зависимость от функции. Выглядит рисунок в виде кривой с асимптотами — прямыми линиями, к которым симметрично стремится гипербола. Однако всем известно, что она никогда их не достигнет. Да, она пересекается возле точки, которая максимально близка к нулю, однако все-таки не достигает ее.

  Именно поэтому многие опытные математики говорят, что при делении на ноль мы получаем бесконечность со знаком плюс или минус (в зависимости от знаменателя). Само собой, можно расписать на бумаге огромное множество решений до тех пор, пока известные числа просто не закончатся. Но стоит ли тратить свою жизнь на то, чтобы делать это? Ведь даже в школе учеников держат подальше от того, чтобы связываться с делением на ноль. Решить такое уравнение попросту невозможно, поскольку существуют миллиарды и даже триллионы возможных решений. Вот такой забавный парадокс с этим нулем.

  
  

  Многие работодатели и авторитетные личности, которые хотят проверить человека с математическим образованием на его знания, попросят доказать принцип бесконечности, на что можно привести эти простые примеры. Ведь каждый высший математик должен не просто знать правило, что на ноль делить нельзя, а уметь объяснить, почему именно решение таких уравнений является бессмысленным.

  Надеемся, теперь вы понимаете, что решение задач, в которых в качестве делителя выступает ноль, неприлично много. Это значит, что пытаться разобрать их будет бессмысленно, поскольку принцип неопределенности попросту не даст довести пример до логического завершения.

  

  Читайте также:

    
  • Как сделать курсы на курсере бесплатными
    
  • Как сделать саше апельсин
    
  • Как сделать сдх
    
  • Как сделать треску под маринадом
    
  • Как сделать своими руками камыши для пруда