Как сделать проекцию на ось в физике
Добавил пользователь Владимир З. Обновлено: 02.09.2024
Если внимательно посмотрим, то увидим, что и т. д.
Таким образом, приходим к формуле:
Словами: пути, проходимые телом за последовательные промежутки времени соотносятся между собой как ряд нечетных чисел, и это не зависит от того, с каким ускорением движется тело. Подчеркнем, что это соотношение справедливо при
3.1.9. Уравнение координаты тела при равнопеременном движении
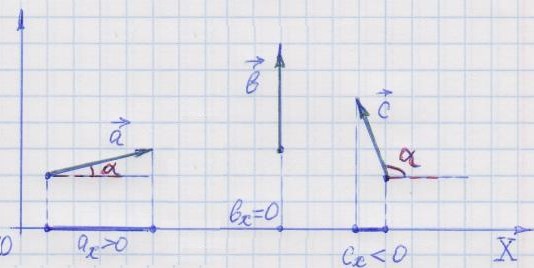
Знаки проекций начальной скорости и ускорения зависят от взаимного расположения соответствующих векторов и оси Ox.
Для решения задач к уравнению необходимо добавлять уравнение изменения проекции скорости на ось:
3.2. Графики кинематических величин при прямолинейном движении
3.3. Свободное падение тела
Под свободным падением подразумевается следующая физическая модель:
1) Падение происходит под действием силы тяжести:
4) Ускорение свободного падения направлено строго вниз и на поверхности Земли равно (в задачах часто принимаем для удобства подсчетов);
3.3.1. Уравнения движения в проекции на ось Oy
В отличии от движения по горизонтальной прямой, когда далеко не всех задач происходит смена направления движения, при свободном падении лучше всего сразу пользоваться уравнениями, записанными в проекциях на ось Oy.
Уравнение координаты тела:
Уравнение проекции скорости:
Как правило, в задачах удобно выбрать ось Oy следующим образом:
Ось Oy направлена вертикально вверх;
Начало координат совпадает с уровнем Земли или самой нижней точкой траектории.
При таком выборе уравнения и перепишутся в следующем виде:
3.4. Движение в плоскости Oxy.
Мы рассмотрели движение тела с ускорением вдоль прямой. Однако этим равнопеременное движение не ограничивается. Например, тело, брошенное под углом к горизонту. В таких задачах необходимо учитывать движение сразу по двум осям:
Или в векторном виде:
И изменение проекции скорости на обе оси:
3.5. Применение понятия производной и интеграла
Мы не будем приводить здесь подробное определение производной и интеграла. Для решения задач нам понадобятся лишь небольшой набор формул.
где A, B и то есть постоянные величины.
то есть скорость является производной от радиус-вектора.
Для проекции скорости:
то есть ускорение является производной от скорости.
Для проекции ускорения:
Таким образом, если известен закон движения то легко можем найти и скорость и ускорение тела.
Теперь воспользуемся понятием интеграла.
то есть, скорость можно найти как интеграл по времени от ускорения.
то есть, радиус-вектор можно найти, взяв интеграл от функции скорости.
Таким образом, если известна функция то легко можем найти и скорость, и закон движения тела.
Константы в формулах определяются из начальных условий — значения и в момент времени
3.6. Треугольник скоростей и треугольник перемещений
3.6.1. Треугольник скоростей
В векторном виде при постоянном ускорении закон изменения скорости имеет вид (3.5):
Эта формула означает, что вектор равен векторной сумме векторов и Векторную сумму всегда можно изобразить на рисунке (см. рис.).
В каждой задаче, в зависимости от условий, треугольник скоростей будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.
3.6.2. Треугольник перемещений
В векторном виде закон движения при постоянном ускорении имеет вид:
При решении задачи можно выбирать систему отсчета наиболее удобным образом, поэтому не теряя общности, можем выбрать систему отсчета так, что то есть начало системы координат помещаем в точку, где в начальный момент находится тело. Тогда
то есть вектор равен векторной сумме векторов и Изобразим на рисунке (см. рис.).
Как и в предыдущем случае в зависимости от условий треугольник перемещений будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.
§ 3. Проекции вектора на оси координат
1. Нахождение проекций геометрически.
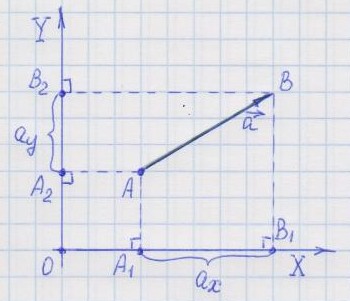
- вектор
- проекция вектора на ось OX
- проекция вектора на ось OY
Определение 1. Проекцией вектора на какую-либо ось координат называется взятое со знаком "плюс" или "минус" число, соответствующее длине отрезка, расположенного между основаниями перпендикуляров, опущенных из начала и конца вектора на ось координат.
Знак проекции определяется так. Если при движении вдоль оси координат происходит перемещение от точки проекции начала вектора к точке проекции конца вектора в положительном направлении оси, то проекция вектора считается положительной. Если же - противоположно оси, то проекция считается отрицательной.
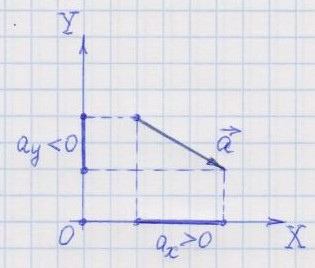
По рисунку видно, что если вектор ориентирован как-то противоположно оси координат, то его проекция на эту ось отрицательна. Если вектор ориентирован как-то в положительном направлении оси координат, то его проекция на эту ось положительна.
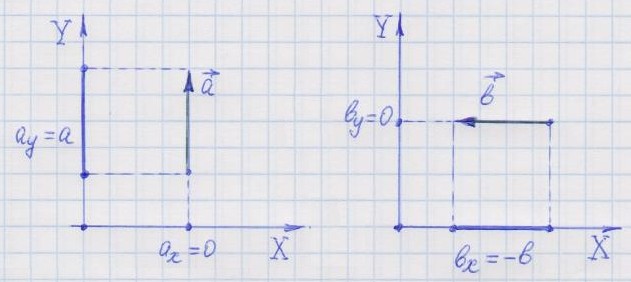
Если вектор перпендикулярен оси координат, то его проекция на эту ось равна нулю.
Если вектор сонаправлен с осью, то его проекция на эту ось равна модулю вектора.
Если вектор противоположно направлен оси координат, то его проекция на эту ось по абсолютной величине равна модулю вектора, взятому со знаком минус.
2. Наиболее общее определение проекции.
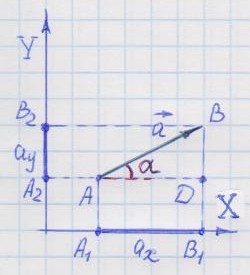
Из прямоугольного треугольника ABD: .
Определение 2. Проекцией вектора на какую-либо ось координат называется число, равное произведению модуля вектора и косинуса угла, образованного вектором с положительным направлением оси координат.
Знак проекции определяется знаком косинуса угла, образованного вектором с положительным направлением оси.
Если угол острый, то косинус имеет положительный знак, и проекции - положительны. Для тупых углов косинус имеет отрицательный знак, поэтому в таких случаях проекции на ось отрицательны.
- поэтому для векторов, перпендикулярных к оси, проекция равна нулю.
Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.
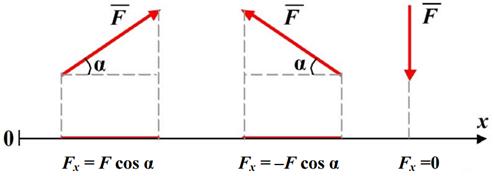
Проекция силы на ось – алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси.
Проекция Fx (рис 1.24) силы на ось х положительна, если угол a острый, отрицательна - если угол a тупой. Если сила перпендикулярна оси, то ее проекция на ось равна нулю.
Проекция силы на плоскость Оху – вектор , заключенный между проекциями начала и конца силы на эту плоскость. Т.е. проекция силы на плоскость величина векторная, характеризуется не только числовым значением, но и направлением в плоскости Оху (рис.1.25).
Тогда модуль проекции на плоскость Оху будет равен:
где a - угол между направлением силы и ее проекцией .
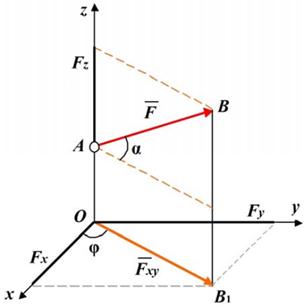
Если сила и ось координат не лежат в одной плоскости, то проекция силы на ось проводится методом двойного проецирования.
Например, чтобы определить проекцию силы на ось х, надо спроецировать ее на плоскость Оху, а затем разложить проекцию силы на составляющие по осям координат Fx и Fy (рис. 1.25):
Закрепленный вектор — упорядоченная пара точек (направленный отрезок, имеющий начало и конец).
Обозначать можем следующими способами: \(\overrightarrow\) , где \(A\) — начало, а \(B\) — конец вектора или просто \(\vec\) .
Длина вектора — расстояние между началом и концом вектора.
Длина векторов обозначается следующим образом: \(|\vec|\) или \(|\overrightarrow|\) .
Если задана прямоугольная система координат, и координаты начала и конца вектора заданы в ней парами \(A=(x_1,y_1)\) и \(B=(x_2,y_2)\) соответственно, тогда координаты вектора можно задать \[\overrightarrow=\\]

Тогда длина вектора \(\overrightarrow\) задается формулой
Проекцией вектора на какую-либо ось называется длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком \(\displaystyle +\) >> или \(\displaystyle -\) >>.

Например, проекцией вектора \(\overrightarrow \) на ось можно считать отрезок \(\displaystyle A'B'\) , взятый со знаком >.
Рассмотрим ситуацию, когда брусок движется по наклонной плоскости:

Исходя из рисунка мы можем записать II закон Ньютона в векторной форме: \[\vec_\text+m\vec+\vec=m\vec\]
Запишем теперь проекции на оси:
Посмотрим, как получили два вышеприведенных равенства. Направим оси, как на рисунке, тогда по оси \(OY\) ускорение и сила трения на тело не действуют, так как они направлены перпендикулярно этой оси, а проекции сил, перпендикулярных оси, равны нулю.
Сила реакции опоры направлена по оси \(OY\) , значит, возьмем ее положительную проекцию.
Также рассмотрим силу тяжести, вектор которой НЕ КОЛЛИНЕАРЕН осям координат, разложим его на два составляющие (см. рисунок сбоку) и возьмем синюю линию, являющуюся проекцией силы тяжести на ось \(OY\) . Из простых геометрических соображений видим, что она равна \(-mg\cos\alpha\) .
Аналогично действуем для оси \(OX\) .
Сложение векторов можно производить по правилу треугольника или по правилу параллелограмма, рассмотрим на примере.

Умножение вектора на число .
Рассмотрим различные варианты произведения вектора \(\vec\) на какое-то вещественное число \(\lambda\) :
При умножении на нулевое число получается нулевой вектор (вектор нулевой длины);
При умножении на положительное число получается вектор, сонапаравленный исходному вектору (происходит просто “удлинение” или “укорачивание” нашего вектора, направление не меняется);
При умножении на отрицательное число получается вектор, противоположно направленный исходному вектору (происходит “разворот” вектора на 180 градусов и изменение его длины одновременно).

Скалярным произведением векторов называют число, равное произведению длин этих векторов на косинус угла между ними.
Физический смысл скалярного произведения
Работу \(A\) тела, перемещаемого из точки \(M\) в \(N\) с постоянной силой \(\vec\) , можно найти как произведение длин векторов \(\vec\) и \(\overrightarrow\) с косинусом угла между ними, значит работа равна скалярному произведению векторов силы и перемещения:

Читайте также:
 webdonsk.ru
webdonsk.ru