Как сделать пирамиду в изометрии
Построение проекции правильной четырехугольной пирамиды начинается с построения основания, горизонтальная проекция которого представляет собой четырехугольник без искажения (рисунок 171, а). Фронтальная проекция основания — отрезок горизонтальной прямой.
Из горизонтальной проекции точки S' (вершины, пирамиды) проводят вертикальную линию связи, на которой от оси х откладывают высоту пирамиды и получают фронтальную проекцию S" вершины. Соединяя точку S" с точками Г', 2", 3" и 4", получают фронтальные проекции ребер пирамиды.
Горизонтальные проекции ребер получают, соединяя горизонтальную проекцию точки S' с горизонтальными проекциями точек Г, 2', 3' и 4'.
Пусть, например, дана фронтальная проекция А" точки А, расположенной на грани пирамиды 1", S", 2" и требуется найти другую проекцию этой точки. Для решения этой задачи проведем через А" вспомогательную прямую, проходящую через вершину пирамиды и точку N",

расположенную на ее грани. Горизонтальную проекцию N'S' вспомогательной прямой находят, применяя линию связи. Искомая горизонтальная проекция А' точки А находится на пересечении линии связи, проведенной из точки А" с горизонтальной проекцией N'S' вспомогательной прямой.
Изометрическая проекция пирамиды выполняется следующим образом (рисунок 171, б).
Вначале строят основание, для чего по оси х откладывают длину диагонали 13, а по оси у — длину диагонали 24. Из точки О пересечения диагоналей проводят ось z и на ней откладывают высоту пирамиды. Вершину S соединяют с вершинами основания прямыми линиями — ребрами.
Изометрическую проекцию точки А, расположенной на грани пирамиды, строят по координатам, которые берут с комплексного чертежа. От начала координат О по оси х откладывают координату хА, из ее конца параллельно оси у — координату уА и из конца этой координаты параллельно оси z — третью координату zA. Построение точки В, расположенной на ребре пирамиды, более простое. От точки О по оси х откладывают координату хв и из конца ее проводят прямую, параллельную оси z, до пересечения с ребром пирамиды в точке В.
.jpg)
- Укажите способы построения аксонометрических проекций и их особенности. Как строят аксонометрические проекции плоских фигур?
- Вы узнаете : как построить прямоугольные изометрические проекции геометрических тел, как найти точки на их поверхностях.
- Вы научитесь: выполнять прямоугольные изометрические проекции геометрических тел, находить точки на их поверхностях.
| Сайт: | Профильное обучение |
| Курс: | Черчение. 10 класс |
| Книга: | § 19. Аксонометрические проекции геометрических тел. Нахождение точек, лежащих на поверхности геометрических тел |
| Напечатано:: | Гость |
| Дата: | Среда, 26 Январь 2022, 06:42 |
Оглавление
Вступление
Геометрические тела правильной формы (многогранники и поверхности вращения) часто встречаются в конструкции деталей машин и механизмов. Правильные геометрические тела характеризуются наличием в них различных осей и плоскостей симметрии, что позволяет строить аксонометрические изображения этих тел по принципу симметрии.
Построение аксонометрических проекций геометрических тел начинают с построения горизонтальной проекции его нижнего основания, к которому достраиваются другие его элементы (грани, ребра, верхнее основание).
Аксонометрические проекции многогранников
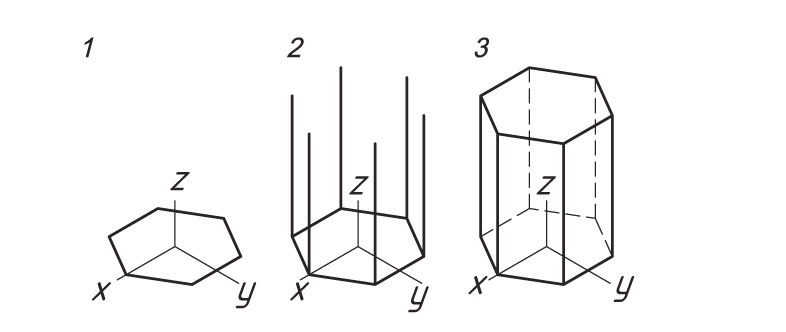
Прямоугольная изометрическая проекция призмы. Основание призмы — правильный многоугольник (например, шестиугольник). Высота призмы совпадает с осью z, а основание расположено в плоскости осей x и y. Размеры призмы определяются их высотой и размерами фигуры основания.
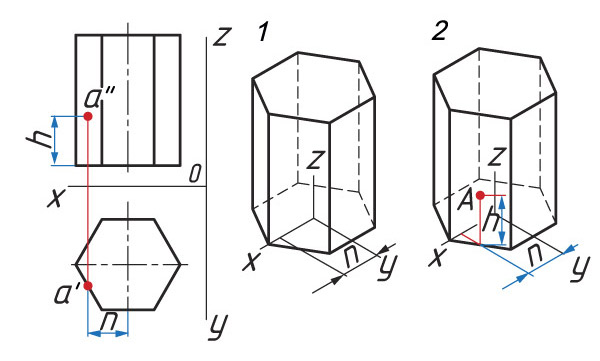
1. Проводят оси изометрической проекции. Затем строят нижнее основание призмы.
2 . Из каждой вершины проводят перпендикуляры, на которых откладывают отрезки, равные высоте призмы.
3. Через полученные точки проводят прямые, параллельные ребрам основания. Определяют видимость ребер.
Определение расположения точки А:
1. От центра основания по оси х проводят прямую хА = n. Из точки n проводят прямую, параллельную оси у, до пересечения с основанием призмы.
2. Из полученной точки параллельно оси z проводят прямую
zА = h.

Определите последовательность построения проекции точки, расположенной на ребре призмы.
Прямоугольная изометрическая проекция пирамиды (например, четырехгранной). Основание пирамиды — ромб. Высота пирамиды (OS) совпадает с осью z, а основание расположено в плоскости осей x и y.
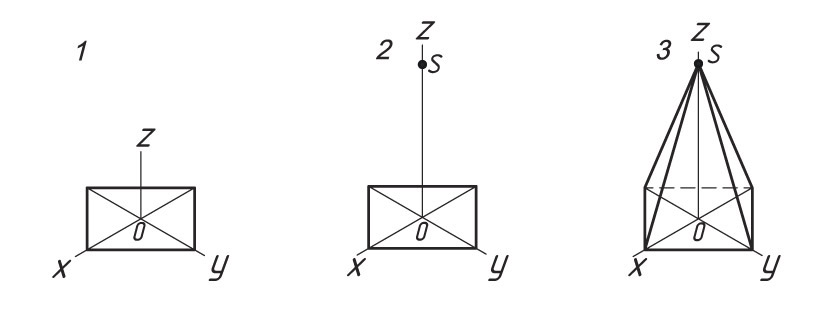
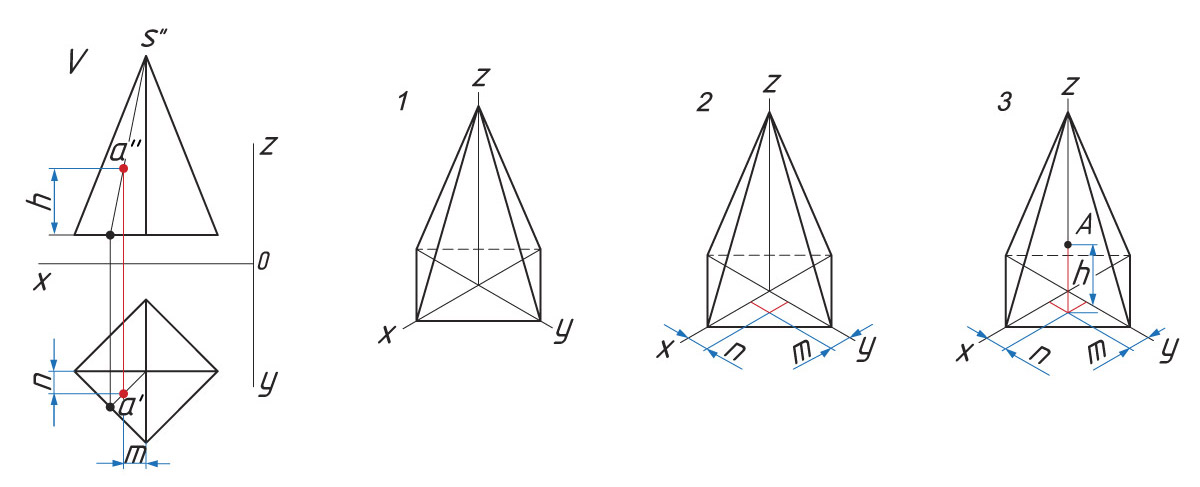
1. Проводят оси изометрической проекции. Размеры пирамиды определяются размерами ее основания и высотой. Затем строят нижнее основание пирамиды, параллельное горизонтальной плоскости.
2. Из центра основания О восстанавливают перпендикуляр, на котором откладывают высоту пирамиды.
3. Соединяют полученную точку S с вершинами основания. Определяют видимость ребер.
Определение расположения точки А
1. От центра основания О по оси х откладывают расстояние хА = m.
2. На оси у откладывают расстояние уА = n.
3. Параллельно оси z проводят отрезок zA = h.
Аксонометрические проекции поверхностей вращения
Окружности, лежащие в основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости проекций. Построение проекций цилиндра и конуса начинают с проведения осей симметрий и построения нижнего основания. Нижнее основание аксонометрических проекций цилиндра и конуса — эллипс.
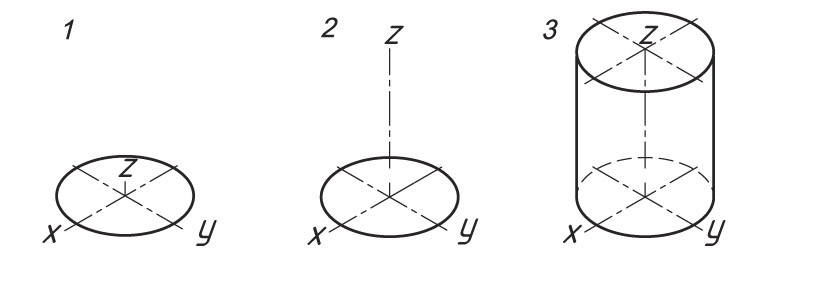
Прямоугольная изометрическая проекция цилиндра. Основание цилиндра — эллипс. Высота цилиндра совпадает с осью z, а основание расположено в плоскости осей x и y. Размеры определяются высотой и диаметром основания.
1. Проводят оси изометрической проекции. Затем строят нижнее основание цилиндра.
2. Из центра основания восстанавливают перпендикуляр и откладывают высоту цилиндра. Строят верхнее основание (эллипс).
3. Проводят боковые образующие цилиндрической поверхности, определяют видимость нижнего основания.
Определение расположения точки А
1. От центра основания по оси х проводят прямую хА= m. Из точки m проводят прямую, параллельную оси у до пересечения с основанием.
2. Из полученной точки параллельно оси z проводят прямую zА= h
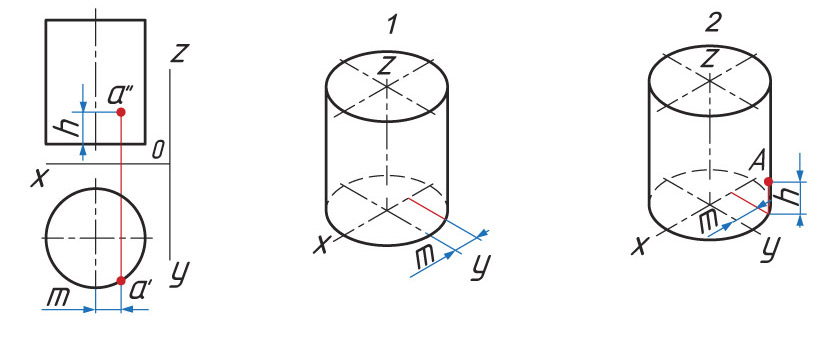

Составьте алгоритм нахождения точки на поверхности цилиндра, учитывая тот факт, что точка расположена на нижнем основании цилиндра.
Прямоугольная изометрическая проекция конуса. Основание конуса — эллипс. Построение проекции конуса схоже с построением проекции цилиндра. Определение расположения точек на поверхности конуса подобно построениям точек на пирамиде.
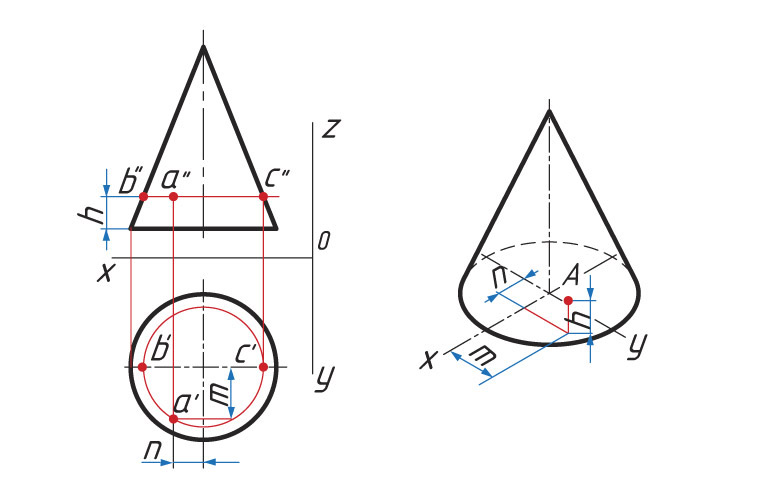

Используя ранее изученный материал, укажите способ нахождения положения точек В и С, изображенный на рисунке.
Проверим знания
1. Что такое показатель (коэффициент) искажения? Какие виды аксонометрии вы знаете? Как располагаются оси прямоугольной изометрии?
2. В какой последовательности выполняют аксонометрическую проекцию геометрического тела?
3. Приведите примеры использования аксонометрических проекций в различных сферах профессиональной деятельности.
4. Мысленно удалите элемент 1, заменив его на элемент 2. Выполните изометрическую проекцию получившейся детали.
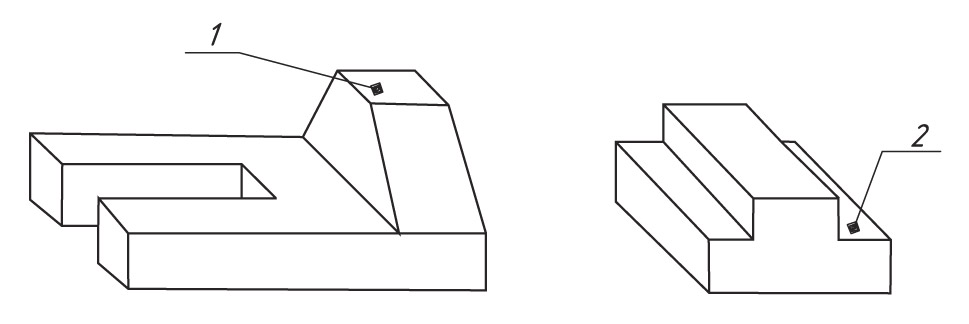
Вопросы и задания повышенной сложности
1. Назовите общие для фронтальной диметрической и изометрической проекций этапы построения цилиндра.
2. Постройте в изометрической проекции правильные треугольную и шестиугольную призмы. Основания призмы расположены горизонтально, длина сторон основания 30 мм, высота 60 мм.
Практическая работа № 10. Аксонометрические проекции геометрических тел
В рабочей тетради выполните по чертежу изометрическую проекцию детали в масштабе 2,5:1. На аксонометрической проекции определите расположение точек А, Б и В.
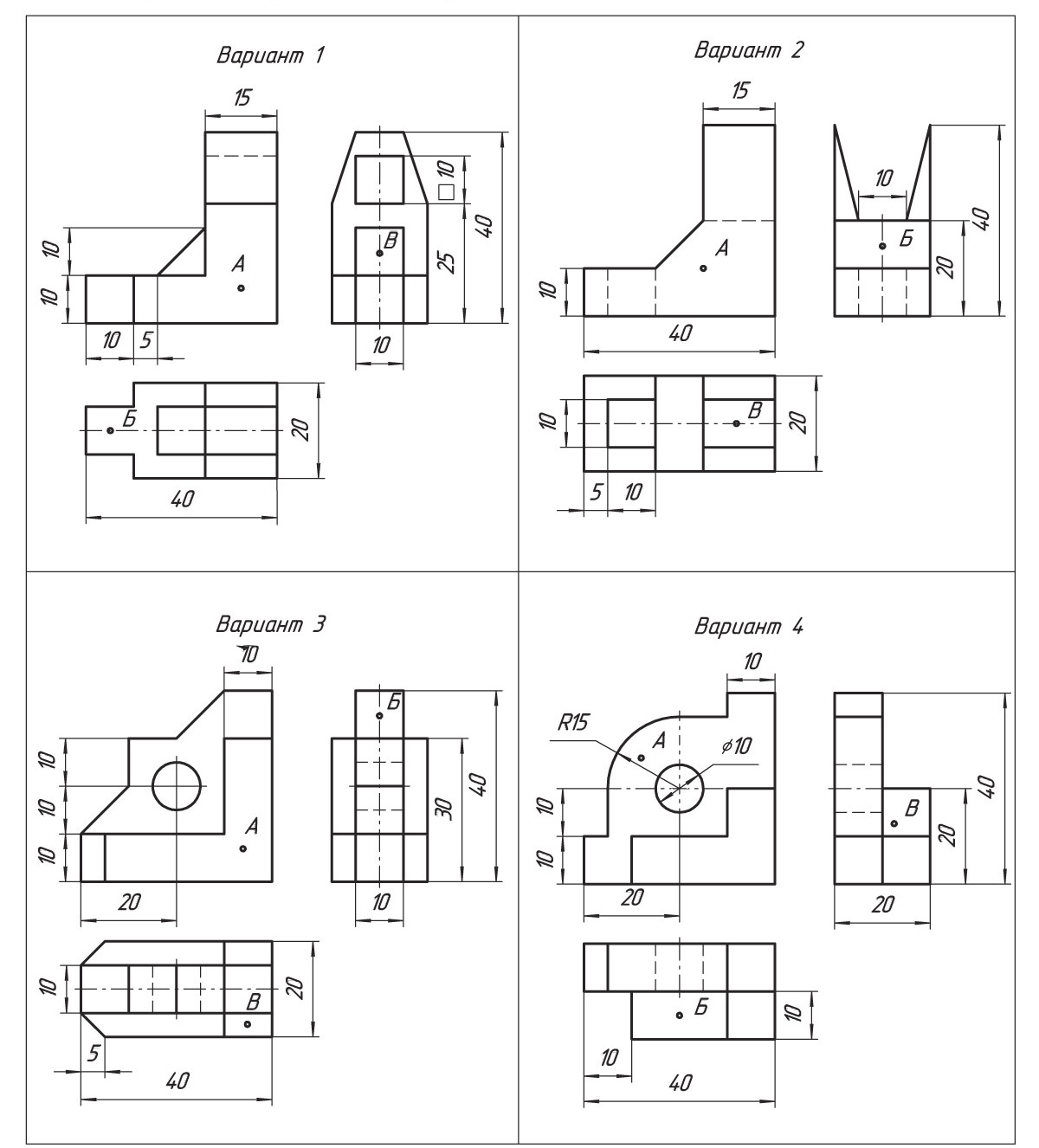
Практическая работа №10.1. Чертеж аксонометрической проекции.
На формате А4 выполнить чертеж детали и аксонометрическую проекцию детали. На аксонометрической проекции покажите точки А, Б, В, Г.
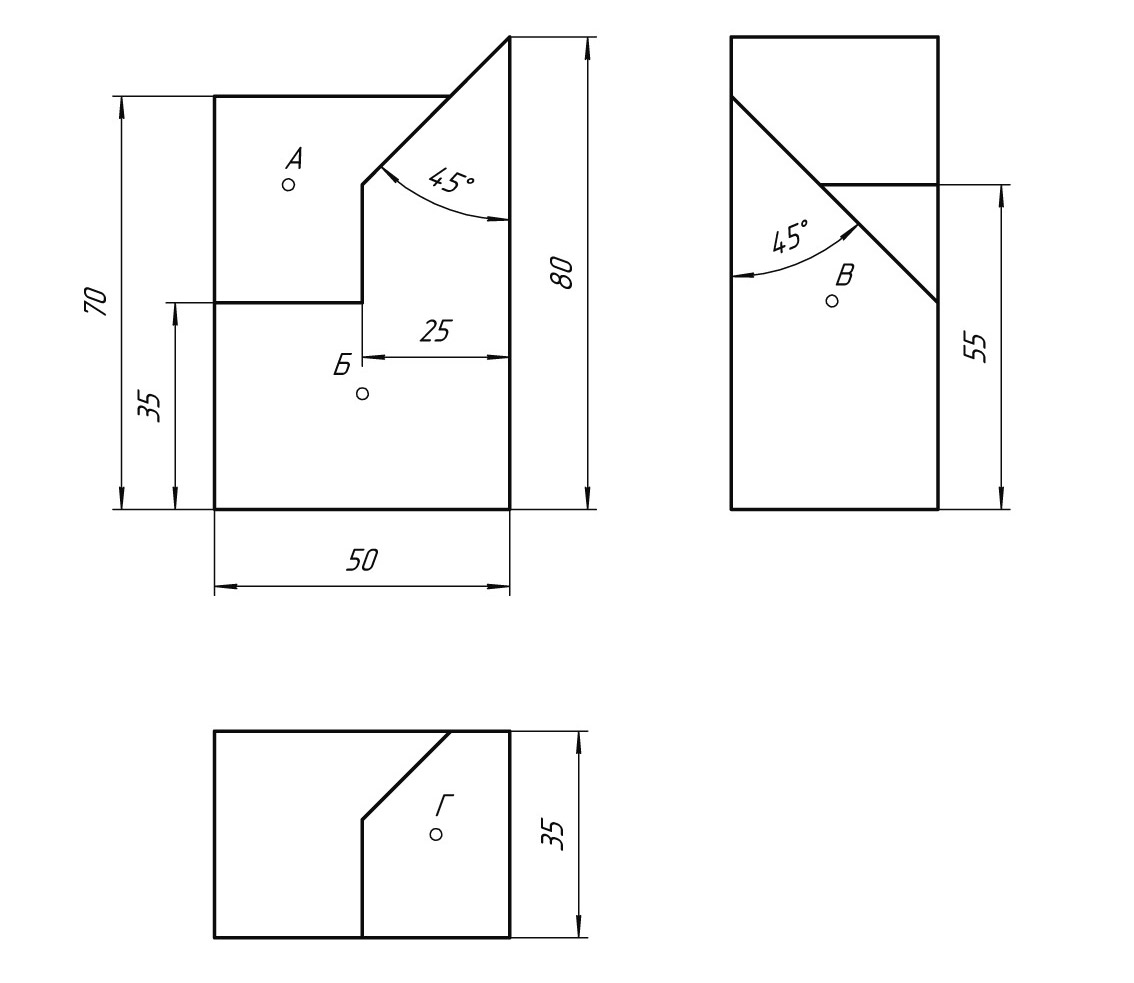
Практическая работа №10.2. Аксонометрическая проекция по чертежу.
Руководствуясь двумя видами на формате А4, выполните чертеж детали в трех проекциях, закончите построение аксонометрической проекции.
Прямоугольная изометрия усеченной пирамиды строится с использованием приведенных коэффициентов искажений: kx = 1; ky = 1; kz = 1.
Начинаем с построения сечения пирамиды плоскостью общего положения a в ортогональных проекциях.

Оно уже выполнено,смотри статью: Сечение пирамиды плоскостью. Чертеж усеченной пирамиды взят оттуда.

Дальнейшие построение аксонометрической проекции Прямоугольная изометрия усеченной пирамиды выполняем по следующему графическому алгоритму: - Относим пирамиду к системе прямоугольных координат x, y и z, оси которой параллельны осям натуральной системы координат, и проходят через высоту пирамиды (ось z) и ее основание (оси x, y); - Определяем в принятой системе координат координаты x, y и z точек сечения 1(x1, y1, z1), 2(x2, y2, z2), 3(x3, y3, z3), 4(x4, y4, z4) и 5(x5, y5, z5) и точек A(xA, yA), B(xB, yB), C(xC, yC), D(xD, yD) и E(xE, yE) - вершин основания пирамиды; - На свободном месте чертежа начертить аксонометрические оси прямоугольной изометрии из произвольно взятой точки O: ось z - вертикально, оси x и y - под углом 120° к вертикальной линии; - Построить тонкими линиями аксонометрическую проекцию пирамиды: - построить аксонометрическое изображение основания пирамиды A0B0C0D0E0 по координатам этих точек; - построить по координате zS вершину пирамиды и соединить ее с вершинами основания - построив тем самым ребра пирамиды. - Построить сечение пирамиды - на ребрах пирамиды точки 1, 2, 3, 4 и 5 по соответствующим координатам: - точку 1 на ребре SA0 - по координатам x1, y1, z1; - точку 2 на ребре SB0 - по координатам x2, y2, z2; - точку 3 на ребре SC0 - по координатам x3, y3, z3; - точку 4 на ребре SD0 - по координатам x4, y4, z4; - точку 5 на ребре SE0 - по координатам x5, y5, z5. - Обвести аксонометрическое изображение пирамиды и ее сечения, выполнив основными линиями ее видимый контур, штриховыми линиями невидимые линии контура, штрихпунктирной линией высоту пирамиды, тонкими линиями полное изображение пирамиды и размерные линии.
Геометрическое тело — часть пространства, ограниченная со всех сторон поверхностью.
Поверхность — это множество всех последовательных положений движущей линии. Эта линия, называемая образующей, при движении может сохранять или изменять свою форму.
Закон перемещения образующей обычно определяется другими линиями, называемыми направляющими, по которым скользит образующая при своем движении.
Рассматривая образование геометрических тел, необходимо отметить, что одно и то же геометрическое тело (а следовательно, и его модель) может быть получено различными способами.
Призма – это фигура, в основании которой лежит многоугольник. Она состоит из верхнего и нижнего оснований (многоугольники), ребер, боковых поверхностей (граней) и вершин.

У пирамиды в основании многоугольник, а ребра сходятся в одной точке – вершине .
Цилиндр – фигура, образуемая вращением отрезка вокруг вертикальной осевой. У цилиндра имеются: верхнее и нижнее основание и боковая поверхность.
Конус образован вращением отрезка вокруг оси по направляющей окружности (основанию). Имеет вершину и боковую поверхность
Проецирование куба и прямоугольного параллелепипеда.

Куб располагают так, чтобы его грани были параллельны плоскости проекции. Проекциями куба являются три равных квадрата (рис.1). На чертеже куба и параллелепипеда указывают три размера: длину, высоту, ширину.
Рис.1 Куб и параллелепипед
а - проецирование; б - чертеж в системе прямоугольных проекций; в,д - изометрические проекции
Проецирование правильных треугольников и шестиугольной призмы

Основания призмы, параллельные горизонтальной плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях – отрезками прямых. Боковые грани изображаются без искажения на тех плоскостях проекций, которым они параллельны, и в виде отрезков прямых на тех, которым они перпендикулярны (рис.2).
Размеры призм определяются их высотой и размерами фигуры основания. Штрихпунктирными линиями на чертеже проведены оси симметрии. Строить изометрические проекции призмы начинают с основания. Затем из каждой вершины основания проводят перпендикуляры, на которых откладывают отрезки, равные высоте, и через полученные точки проводят прямые, параллельные ребрам основания. Чертеж в системе прямоугольных проекций также начинают выполнять с горизонтальной проекции.
Рис.2 Призмы
а,г – проецирование;
б,д – чертежи в системе прямоугольных проекций;
в,е – изометрические проекции .
Проецирование правильной четырехугольной пирамиды.

Квадратное основание пирамиды проецируется на горизонтальную плоскость Н в натуральную величину. На нем диагоналями изображаются боковые ребра, идущие от вершин основания к вершине пирамиды (рис.3). Фронтальная и профильная проекции пирамиды – равнобедренные треугольники. Размеры
пирамиды определяются длиной двух сторон ее основания и высотой. Изометрическую проекцию пирамиды начинают строить с основания. Из центра полученной фигуры проводят перпендикуляр, откладывают на нем высоту пирамиды и соединяют полученную точку с вершинами основания.
Рис.3 Пирамида
а – проецирование; б чертеж в системе прямоугольных проекций;
в – изометрическая проекция.

4. Проецирование цилиндра и конуса.
Если круги, лежащие в основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости Н, их проекции на эту плоскость будут также кругами ( рис.4) Фронтальная и профильная проекции в этом случае – прямоугольники, а конуса - равнобедренные треугольники. Они одинаковы.
Рис.4 Цилиндр и конус
а,г – проецирование;
б,д – чертежи в системе прямоугольных проекций;
в, е – изометрические проекции
Проекции шара
Все проекции шара – круги, диаметр которых равен диаметру шара ( рис.5). На каждой проекции проводят центровые линии.

Рис.5 Проекции шара
Контрольные вопросы
1. В какой последовательности строят проекции прямого кругового цилиндра и правильной шестигранной призмы, основания которых расположены на фронтальной плоскости?
2. Что является горизонтальной проекцией конуса?
3. Что является профильной проекцией конуса и четырехугольной пирамиды?
4. По каким правилам производится проецирование на плоскости проекций? Что такое линия связи?
5. Алгоритм построения трех проекций геометрических тел.
© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.004)

Читайте также:
