Как сделать отбор корней в тригонометрических уравнениях по окружности

Добавил пользователь Валентин П.
Обновлено: 03.10.2024

Решение простейших тригонометрических уравнений

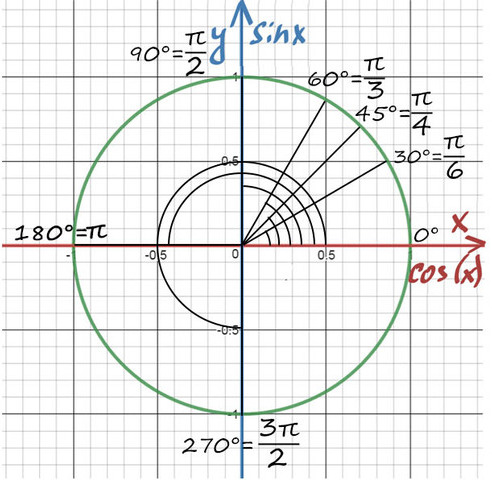
Градусы и радианы

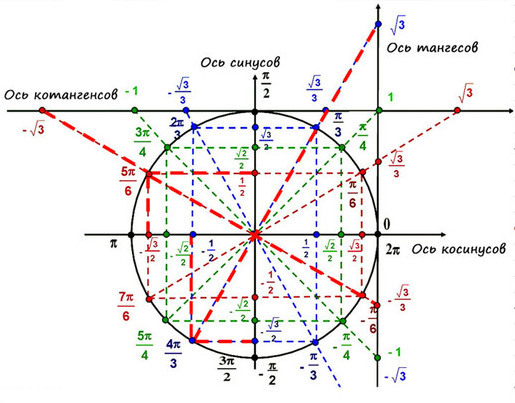
Знакомство с тригонометрической окружностью

Повороты на тригонометрической окружности

Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах .

1 радиан = 180/p ? 57,3 градусов

Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа p.

Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на p!

О графиках синуса, косинуса и тангеса поговорим в другой статье.

А сейчас начем с декартовой (прямоугольной) системы координат.

Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.

На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:

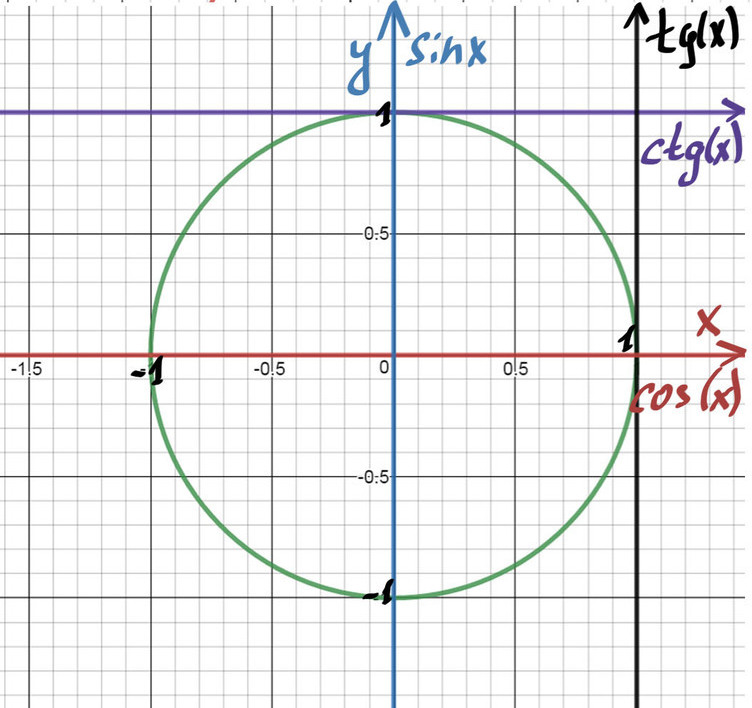
Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.

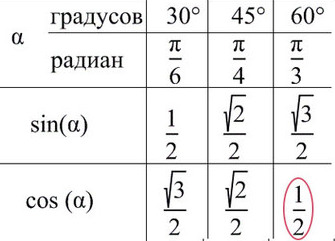
А теперь отметим основные значения градусов и радиан на окружности.

Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.

Достаточно запомнить, что p = 180° (тогда p/6 = 180/6 = 30°; p/3 = 180/3 = 60°; p/4 = 180/4 = 45°).

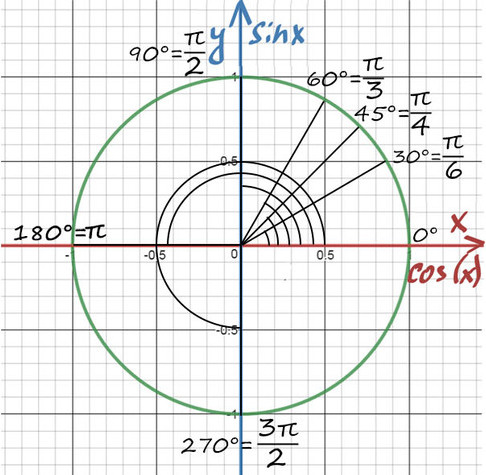
А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):

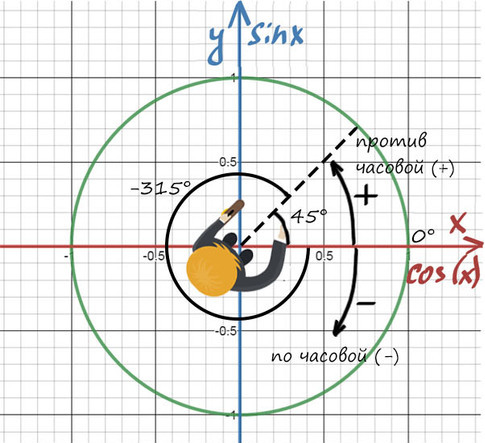
От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).

Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).

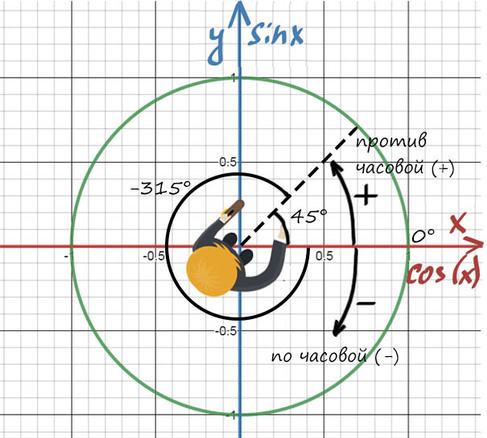
Главное — направление, куда мы будем смотреть, а не угол!

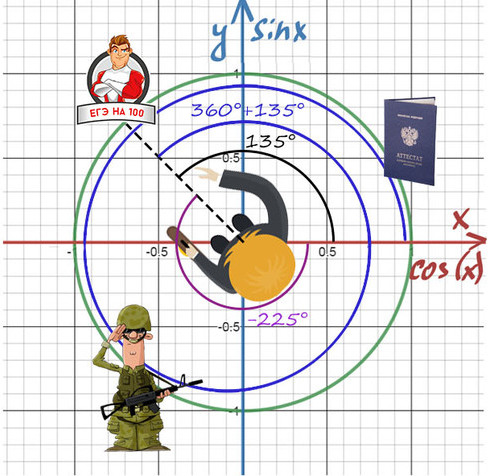
Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°.

А теперь у тебя есть два пути:

Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:

А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.

Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.

Сразу попробуем разобрать на примере:

1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение 1/2 и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.

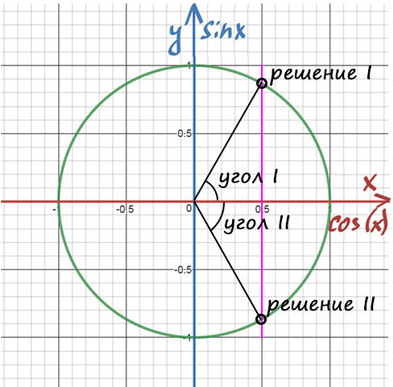
2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.

Дело за малым — найти эти углы.

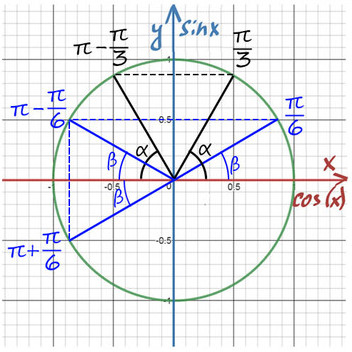
Или запомнить такой прием:

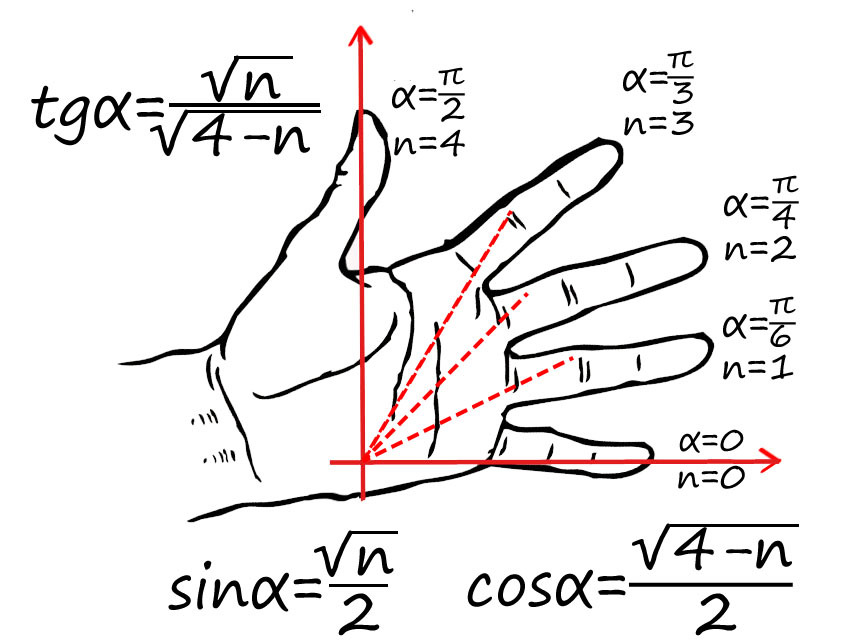
Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).

Например, требуется найти sin(p/2) : p/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(p/2) = ?4/2 = 1 => sin(p/2) = 1.

cos(p/4) - ? p/4 соответсвует среднему пальцу (n = 2) => cos(p/4) = ?2/2.

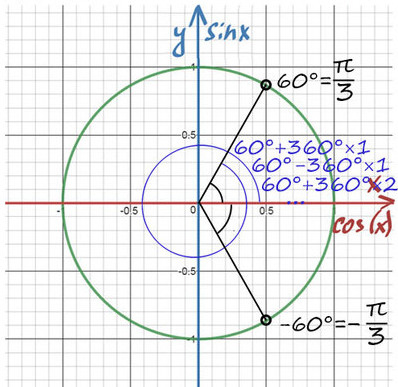
При значении cos(x) = 1/2 из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +p/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).

Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (-). x = -p/3 (угол показан нижней черной дугой).

И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:

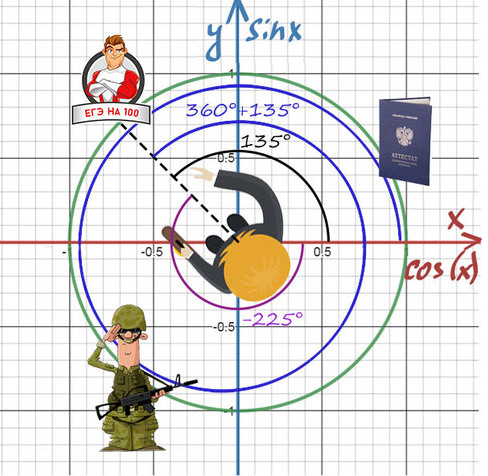
То же самое и здесь! Разные углы могут отражать одно и то же направление.

Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2p (синим цветом) сколько угодно раз и в любом направлении.

Таким образом, попасть в первое направление 60° можно: . 60°-360°, 60°, 60°+360°.

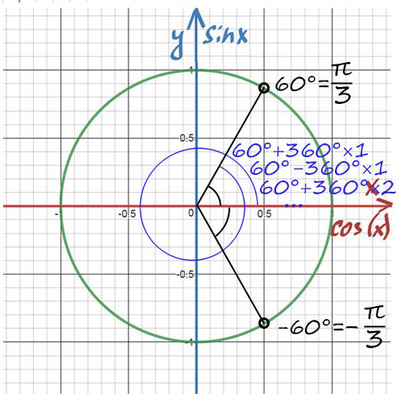
И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть?)

Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n?Z) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = -60 + 360n.

Но мы же договорились, что на окружности все записывают через p, поэтому cos(x) = 1/2 при x = p/3 + 2pn, n?Z и x = -p/3 + 2pk, k?Z.

Ответ: x = p/3 + 2pn, x= - p/3 + 2pk, (n, k) ?Z.

Пример №2. 2sinx = ?2

Первое, что следует сделать, это перенести 2-ку вправо => sinx=?2/2

1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем ?2/2 и проводим ? фиолетовую прямую до пересечений с окружностью.

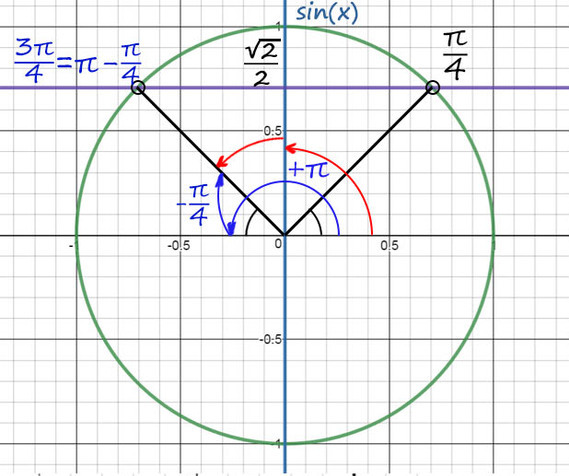
2) Из таблицы sinx = ?2/2 при х = p/4, а вторую точку будем искать с помощью поворота до p, а затем нужно вернуться обратно на p/4.

Поэтому вторая точка будет x = p - p/4 = 3p/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.

И еще не забудем добавить +2pn, n?Z.

Ответ: 3p/4 + 2pn и p/4 + 2pk, k и n - любые целые числа.

Пример №3. tg(x + p/4) = ?3

Вроде все верно, тангенс равняется числу, но смущает p/4 в тангенсе. Тогда сделаем замену: y = x + p/4.

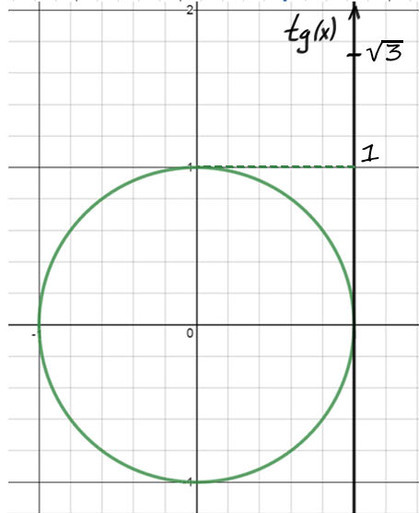
tg(y) = ?3 выглядит уже не так страшно. Вспомним, где ось тангенсов.

1) А теперь на оси тангенсов отметим значение ?3, это выше чем 1.

2) Проведем фиолетовую прямую через значение ?3 и начало координат. Опять на пересечении с окружностью получается 2 точки.

По мнемоническому правилу при тангенсе ?3 первое значение — это p/3.

3) Чтобы попасть во вторую точку, можно к первой точке (p/3) прибавить p => y = p/3 + p = 4p/3.

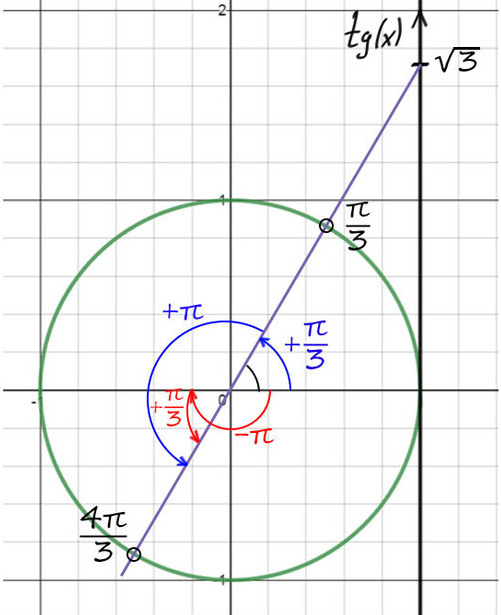
4) Но мы нашли только y , вернемся к х. y = p/3 + 2pn и y = x + p/4, тогда x + p/4 = p/3 + 2pn => x = p/12 + 2pn, n?Z.

Второй корень: y = 4p/3 + 2pk и y = x + p/4, тогда x + p/4 = 4p/3 + 2pk => x = 13p/12 + 2pk, k?Z.

Теперь корни на окружности будут здесь:

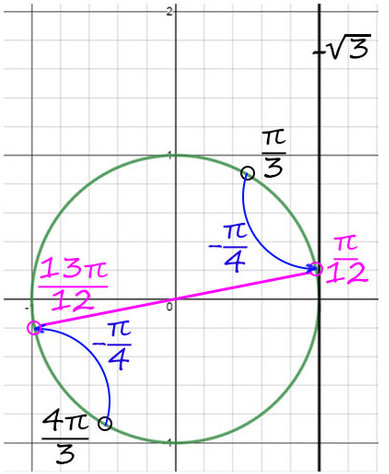
Ответ: p/12 + 2pn и 13p/12 + 2pk, k и n — любые целые числа.

Конечно, эти два ответа можно объединить в один. От 0 поворот на p/12, а дальше каждый корень будет повторяться через каждый p (180°).

Ответ можно записать и так: p/12 + pn, n?Z.

Пример №4: -10ctg(x) = 10

Перенесем (-10) в другую часть: ctg(x) = -1. Отметим значение -1 на оси котангенсов.

1) Проведем прямую через эту точку и начало координат.

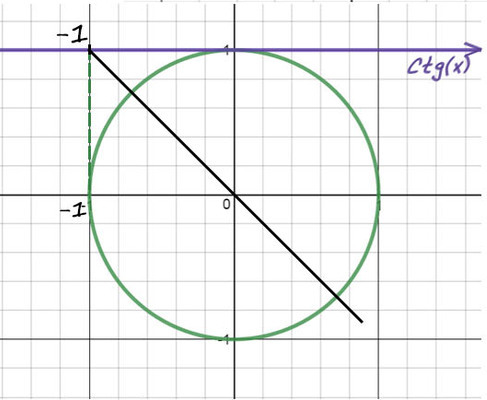
2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при p/4). Но здесь -1, поэтому одна точка будет -p/4. А вторую найдем поворотом до p, а потом назад на p/4 (p - p/4).

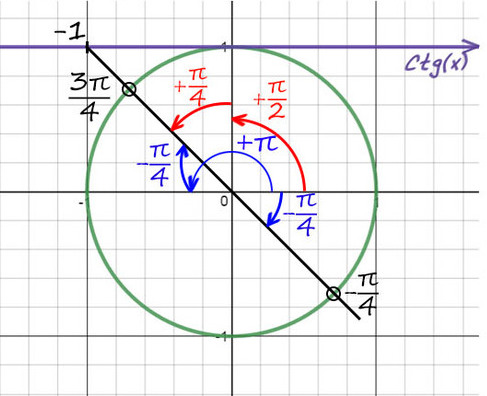
Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (p, 2p, 3p. ) так намного меньше шансов запутаться.

Не забываем добавить к каждой точке 2pk.

Ответ: 3p/4 + 2pn и -p/4 + 2pk, k и n — любые целые числа.

Алгоритм решения тригонометрических уравнений (на примере cos(x) = - ? 3/2) :

В задаче 13 профильного ЕГЭ по математике часто встречается тригонометрическое уравнение, которое необходимо решить и указать корни, принадлежащие заданному промежутку. Наиболее простой способ отбора корней из промежутка — графически на тригонометрическом круге. Если же промежуток большой (больше одного оборота), имеет нестандартные границы или решение тригонометрического уравнения имеет большой период, то целесообразно проводить отбор корней уравнения из промежутка с помощью неравенства.

Пример 1. Отобрать корни уравнения из заданного промежутка

Пример 2. Отобрать корни уравнения из заданного промежутка

Задания для самостоятельного решения

Пример 3. Отобрать корни уравнения из заданного промежутка

Пример 4. Отобрать корни уравнения из заданного промежутка

Задание для контроля

Пример 5. Отобрать корни уравнения из заданного промежутка

Запись ответа в работе участника экзамена может отличаться от приведенной в критериях (содержать один целочисленный параметр n или несколько k , m , n ). Важно, чтобы в ответе были приведены все ответы для пункта а .

Пример задания 13 из вариантов ЕГЭ 2018 (профильный уровень)

Критерии проверки задания 13

Содержание критерия

Обоснованно получены верные ответы в обоих пунктах

Обоснованно получен верный ответ в пункте а

Решение не соответствует ни одному из критериев, перечисленных выше

получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов – пункта а и пункта б

Прежде чем приступать к решению заданий 13, нужно запомнить и научиться применять формулы записи решений простейших тригонометрических уравнений и далее овладеть методами решения основных типов тригонометрических уравнений.

Следует обратить внимание учащихся, что в случае отбора корней использование общей формулы серии решений для синуса и косинуса не всегда является удобной.

При выполнении пункта б задания 13 удобнее не объединять серии решений, а наоборот - представлять их совокупностью.

Серии решений, записанные через совокупности

Нюансы начальной подготовки к овладению методами решения задания 13

1. По возможности при выполнении пункта б задания не использовать запись

Эта запись не показывает: во-первых, что серий решений две;

во-вторых, что период синуса .

Отбирать корни при такой форме записи крайне неудобно.

Замечание . В случае использования этих формул нужно отметить на оси синусов значение а и получить на тригонометрической окружности две точки.

2. Давать отдельные задачи на отбор корней без решения уравнений.

Нюансы начальной подготовки к овладению методами решения задания 13

3. Учиться проверять ответ. Для этого задавать вопрос:

«Сколько корней данная серия решений

4. Начинать обучение с заданий на отработку методов решений уравнений и способов отбора корней, в которых первична идейная часть, а вычислительная часть достаточно проста.

5. Самоконтроль! Прежде чем записывать окончательный ответ, убедиться еще раз в верности корней их непосредственной подстановкой в исходное уравнение.

Методы решения тригонометрических уравнений

При решения тригонометрических уравнений обычно используют один из следующих методов:

равносильных преобразований с применением формул;
замены, сведение к алгебраическому уравнению;
разложение на множители;
метод вспомогательного аргумента (линейные уравнения);
функциональный.

Методы решения тригонометрических уравнений

Рекомендации по оформлению решения задания 13 на экзамене

Задание 13 (С1). Задание содержит два пункта:

а) решить тригонометрическое уравнение,

б) отобрать его корни на данном промежутке.

Соответственно в ответе должно быть две части:

а) все корни уравнения (не забудьте написать n?Z ),

б) отобранные на данном промежутке корни.

Решение уравнения лучше никак не комментировать и не писать знаков равносильности, так как часто при верном решении выпускники ошибаются в комментариях и ставят проверяющих в тупик.

Отбор корней , можно проводить разными способами, но рекомендуется его провести на окружности. При этом в начале отбора стоит написать фразу: отберем корни с помощью единичной окружности и затем на окружности обязательно все обозначить: точки – концы промежутка (в данном случае дуги), сами корни и жирным выделить саму дугу. Этот рисунок рисуется не для себя, а для проверяющего, на нем все должно быть видно.

Методы отбора корней тригонометрических уравнений

При решения тригонометрических уравнений в случаях

отбора корней обычно используют один из следующих

арифметический;
алгебраический;
геометрический (на тригонометрической

окружности или числовой прямой);

Арифметический метод отбора корней

тригонометрических уравнений

Арифметический метод отбора корней связан с вычислением корней при переборе значений целочисленного параметра или нахождением значений тригонометрических выражений непосредственной подстановкой при проверке корней.

а) непосредственная подстановка полученных корней в уравнение и имеющиеся ограничения;

б) перебор значений целочисленного параметра и вычисление корней.

Замечание. В решении должна присутствовать оценка возможных значений целочисленного параметра.

Отбор корней непосредственной подстановкой

Алгебраический метод отбора корней

Алгебраический метод отбора корней удобен в тех случаях, когда:

– последовательный перебор значений параметров приводит к вычислительным трудностям;

– промежуток для отбора корней большой;

– значения обратных тригонометрических функций, входящих в серии решений, не являются табличными;

– при решении задач с дополнительными условиями.

Алгебраический метод – это:

а) решение неравенства относительно целочисленного параметра и вычисление корней;

б) исследование уравнения с двумя целочис ленными параметрами.

Геометрический метод отбора корней

Геометрический способ отбора корней предполагает наличие у учащихся навыков изображения решения простейших тригонометри-ческих уравнений и неравенств на числовой окружности или прямой, поэтому необходимо напомнить им основные действия с точками числовой окружности, связанные с формулами решений простейших тригонометрических уравнений.

Геометрический способ предполагает:

а) изображение корней на тригонометрической окружности и их отбор с учетом имеющихся ограничений;

б) изображение корней на числовой прямой с последующим отбором и учетом имеющихся ограничений.

Решение задания 13 с отбором корней на окружности

Отбор корней на числовой прямой

Геометрический метод отбора корней

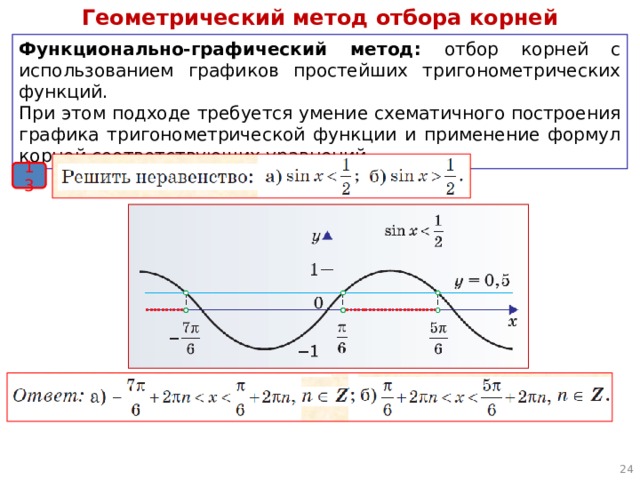
Функционально-графический метод: отбор корней с использованием графиков простейших тригонометрических функций.

При этом подходе требуется умение схематичного построения графика тригонометрической функции и применение формул корней соответствующих уравнений.

Функционально-графический метод отбора корней

Метод замены

Если уравнение приводится к виду можно сделав замену , решить уравнение относительно t , а затем решить полученные уравнения с относительно .

б) Укажите корни, принадлежащие отрезку [-p; 2p].

Решение:

б) Теперь будем искать корни, принадлежащие отрезку [-p; 2p].

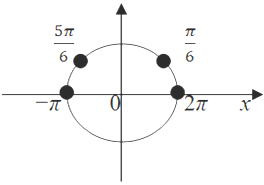
Рассмотрим 3 способа отбора корней:

Этот способ наиболее точный и если учащиеся владеют навыками решения двойного неравенства, то понятный и подходит совершенно всем и в любых случаях.

a) На окружности найдем края отрезка: точки –p и 2p.

б) Смотрим на точки — из каких серий решения попали в этот отрезок.

в) Выбираем эти точки.

Если данные отрезки бывают длиной больше 2p, тогда можно потерять некоторые корни, поэтому рекомендуется: нарисовать вторую концентрическую окружность, будто соответствующую следующему периоду (это просто модель, которая помогает решить задачу). Этот способ хорошо дается тем, кто умеет определять на окружности точки и отсчитывать периоды.

а) Чертим график у = sinx;

в) Проводим прямую у = $\frac$;

г) Отмечаем точки с ординатой $\frac$ на искомом отрезке, получаем х = $\frac<\pi>$ и 5 · $\frac<\pi>$.

Способ очень наглядный и подойдет тем, кто не усвоил вышеизложенные два способа.

Читайте также: