Как сделать обратное дифференцирование

Добавил пользователь Алексей Ф.
Обновлено: 09.09.2024

Формула обратного дифференцирования ( BDF ) - это семейство неявных методов численного интегрирования обыкновенных дифференциальных уравнений . Это линейные многоступенчатые методы, которые для данной функции и времени аппроксимируют производную этой функции, используя информацию из уже вычисленных моментов времени, тем самым повышая точность приближения. Эти методы особенно используются для решения жестких дифференциальных уравнений . Впервые эти методы были введены Чарльзом Ф. Кертиссом и Джозефом О. Хиршфельдером в 1952 году.

СОДЕРЖАНИЕ

Общая формула

BDF используется для решения задачи начального значения

у ? знак равно ж ( т , у ) , у ( т 0 ) знак равно у 0 . ) = y_ .>

Общая формула для BDF может быть записана как

? k знак равно 0 s а k у п + k знак равно час v ж ( т п + s , у п + s ) , ^ a_ y_ = h \ beta f (t_ , y_ ),>

где обозначает размер шага, а . Поскольку вычисляется неизвестное , методы BDF являются неявными и, возможно, требуют решения нелинейных уравнений на каждом шаге. Коэффициенты и выбираются таким образом, чтобы метод достиг максимально возможного порядка . час т п знак равно т 0 + п час = t_ + nh> ж у п + s > а k > v s

Вывод коэффициентов

Конкретные формулы

S -шагового с без рецидива с у п + 1 - у п знак равно час ж ( т п + 1 , у п + 1 ) -y_ = hf (t_ , y_ )>

Методы с s > 6 не являются устойчивыми к нулю, поэтому их нельзя использовать.

Стабильность

Об устойчивости численных методов решения жестких уравнений свидетельствует их область абсолютной устойчивости. Для методов BDF эти области показаны на графиках ниже.

В идеале область содержит левую половину комплексной плоскости, и в этом случае метод называется A-устойчивым. Однако линейные многоступенчатые методы порядка больше 2 не могут быть A-стабильными . Область устойчивости методов BDF более высокого порядка содержит большую часть левой полуплоскости и, в частности, всю отрицательную действительную ось. Методы BDF являются наиболее эффективными линейными многоступенчатыми методами такого рода.

Пусть функция \(u=g(x)\) определена на множестве \(X\), и \(U\) — область её значений.
Пусть далее функция \(y=f(u)\) определена на множестве \(U\).
Поставим в соответствие каждому \(x\) из \(X\) число \(f(g(x))\).
Говорят, что на множестве \(X\) задана сложная функция \(y=f(g(x))\).

Если известна производная функции \(f(x)\), то производную сложной функции \(f(u)\) можно вычислить с помощью следующей формулы:

Так как x 10 ? = 10 x 9 , то x + 2 10 ? = ( u 10 ) ? = 10 u 9 ? u ? = 10 x + 2 9 ? 1 = 10 x + 2 9 .

( sin ( cos x ) ) ? = ( sin u ) ? = cos u ? u ? = = cos ( cos x ) ? ( cos x ) ? = = cos ( cos x ) ? ( - sin x ) = = - cos ( cos x ) ? sin x .

Автоматическое дифференцирование (AD) является одной из движущих сил истории успеха Deep Learning. Это позволяет нам эффективно рассчитывать оценки градиента для наших любимых составных функций. TensorFlow, PyTorch и все его предшественники используют AD. Вдобавок к методам стохастической аппроксимации, таким как SGD (и все его варианты), эти градиенты улучшают параметры наших любимых сетевых архитектур.

Многие люди (до недавнего времени включая меня) считают, что обратное распространение, правило цепочки и автоматическое дифференцирование являются синонимами. Но это не так. Чтобы стать настоящими мастерами ремесла, нужно разобраться, почему. ?

TL; DR:Мы обсуждаем различные способы дифференциации компьютерных программ. Более конкретно, мы сравним автоматическое дифференцирование в прямом и обратном режимах (backprop). В конечном итоге мы реализуем прямой режим AD с двойными числами для простой задачи логистической регрессии. Простой кодекс можно найтиВот,

Аналитическое выражение может быть легко переведено в некоторый код Python:

Функция вычисляет числовое значение на основе фиксированных истинных меток ( y_true ) и прогнозируемые / подогнанные вероятности маркировки ( y_pred ). В нашем случае y_pred составляет сигмоидно-сжатый выход, который снова является функцией v. Чтобы найти наилучшие подходящие коэффициенты, нам нужно следовать направлению наискорейшего спуска (градиент), которое минимизирует функцию потерь. Для этого у нас есть доступ к набору методов дифференциации:

В своей основе AD объединяет лучшее из числового и символического миров. Он вычисляет значение производной с помощью элементарного правила, установленного из символического дифференцирования. Чтобы преодолеть отек, символическое выражение упрощается на каждом этапе. Просто путем численной оценки с результатами предыдущих вычислений (или просто входных данных). Следовательно, он не дает аналитического выражения для самой производной. Вместо этого он итеративно оценивает данные по градиенту. Проще говоря: f ’(2) ? f’ (x).

Давайте посмотрим, как это относится к нашей проблеме логистической регрессии, и определим пошаговые выходы как a (h) = s (h) и h (X, v) = X v. Затем мы можем переписать градиент интереса как:

Выражение выше является производным от руки. На первый взгляд это может не выглядеть как упрощение Но теперь мы можем наблюдать более общий принцип: градиент может быть разложен на компоненты градиента отдельного пути преобразования:

Предварительные активации h (X, v) и их градиент ?h (X, v) по параметрам v.
Активации a (h) и их градиент ?a (h) по сравнению с предварительными активациями h.
Журнал зондирования классов log a (h) и диагональная матрица градиента ?log a (h) относительно активаций a.

Для каждой частичной оценки h (X, v), a (h), log a (h) мы можем легко вычислить чувствительность к их соответствующим входам v, h, a и получить их производные. В конечном счете, вектор истинной вероятности p обеспечивает сигнал ошибки, который масштабирует градиент.

Мы можем перейти кавтоматическирассчитать отдельные компоненты градиента двумя различными способами:

Наконец, общий градиент ?Lзатем получается путем умножения отдельных частей вместе и масштабирования с р.

При сравнении режимов работы необходимо учитывать два основных момента:

Мы заинтересованы в продвижении вычислений от нескольких единиц ко многим. Вещи не обязательно такие четкие, поскольку можно довольно легко векторизовать вычисления в прямом режиме. Следовательно, никаких отдельных прямых пропусков не требуется. Я предполагаю, что доминирование обратного режима в DL происходит в основном из-за снижения требований к памяти.

Итак, здесь идет алгебраический фокус, который упрощает прямой режим AD: можно показать, что прямой режим AD эквивалентен оценке интересующей функции с помощью двойных чисел.

Моя мотивация для этого поста в блоге проистекала из неудовлетворенности моим пониманием именно этой эквивалентности. Поэтому мне пришлось копать немного глубже. Позвольте мне теперь попытаться пролить свет на элегантность использования двойной части любой числовой оценки для вычисления градиентов соответствующих параметров. Так что же такое двойные числа? Мы можем разложить входную переменную x на вещественную и на двойную часть:

с v, v? действительными числами, ? ? 0 и e? = 0. На основе этого простого определения получаются следующие основные арифметические свойства:

Кроме того, можно алгебраически вывести следующее:

Вот Это Да! Оценив f (x) в его двойной форме и установив v? = 1, мы можем восстановить как значение функции f (v), так и его вычисленную производную f ’(v) в виде коэффициента перед e! Наконец, правило цепочки плавно переводится в двойную настройку:

Это означает, что мы можем легко распространять градиенты по уровням вычислений, просто умножая производные друг на друга. Для реализации двойных чисел нам просто требуется отдельная система хранения, которая отслеживает x = (v, coeff-in-front-of-v?) и применяет соответствующие производные вычисления к двойной части x Потрясающая алгебра!

Для многомерных функций все становится немного сложнее. Представьте себе два входа:

Частная производная по x вычисляется путем установки v = 1 и u = 0. Для вас мы должны перевернуть оба бита. Чтобы сделать это параллельно и предотвратить несколько проходов вперед, мы можем векторизовать вещи и сохранить диагональную матрицу:

с каждой строкой, представляющей одну частную производную. Все вышеперечисленные правила легко переводятся в многомерный случай.

e можно рассматривать как форму бесконечно малого числа. При возведении в квадрат такого небольшого числа это просто становится непредставимым. Интуитивно это похоже на размер шага численного дифференцирования.
Другой возможный способ думать о as - это матрица:

Вычисление x затем дает требуемую нулевую матрицу. Ограничивая мнимые числа i? = -1, помогите нам в вычислении поворотов. Двойные числа, с другой стороны, ограничивают e? = 0 и позволяют эффективно и точно вычислять производную. Давайте посмотрим, как мы можем перевести это в код для нашего примера логистической регрессии.

Во-первых, нам нужны некоторые синтетические данные для нашей проблемы двоичной классификации. Объект класса ниже генерирует коэффициенты, гауссовский шум и особенности. После этого мы берем скалярное произведение и порождаем преобразованные функции, чтобы получить двоичные метки. Кроме того, есть несколько небольших утилит для выборки пакетов данных и перетасовки данных между эпохами. Все довольно стандартные вещи. Ничего двойственного.

Двойная версия сигмоидальной функции применяет стандарт s к действительной части и изменяет числовое значение двойной матрицы размерности n x d с ее оцененной производной. Поскольку s ’(h) = s (h) (1 - s) применяется к каждому элементу вектора h. Следовательно, общее изменение двойной части определяется как:

Что снова приводит к якобиану размера n x d. То же самое относится к оператору журнала. Теперь, когда мы получили переопределенные параметры арифметики для наших операций с двумя числами, давайте рассмотрим, как мы можем получить наши прогнозы логистической регрессии и соответствующую двоичную кросс-энтропийную потерю:

Наконец, давайте соберем все вместе в заключительном цикле обучения. Мы генерируем двоичные данные и инициализируем некоторые списки заполнителей для хранения наших промежуточных результатов. После этого мы вычисляем коэффициенты решения Склеарна, чтобы измерить, как далеко мы находимся. Тогда мы можем просто перебрать отдельные партии. Мы инициализируем коэффициенты как двойной тензор, образцы пакетов, устанавливаем коэффициенты градиента / диагональную матрицу обратно к их частичной инициализации производной. Получаем прогнозы и потери. Двойник оценки потерь соответствует градиенту интереса ?L, Обновления SGD тогда просто берут двойное и выполняют шаг в самом крутом направлении снижения.

Давайте обучим простой пример и посмотрим на метрики:

Мы уже обсуждали, почему обратное распространение и обратный режим AD более эффективны для стандартных приложений глубокого обучения. Одной из причин, почему AD по-прежнему может пригодиться в прямом режиме, является его полезность в вычислении векторно-гессианских продуктов Hv. Мы можем использоватьобращенно-на-впередКонфигурация для объединения как прямого, так и обратного режимов для вычисления гессиана 2-го порядка. Более конкретно, учитывая функцию f с входом x, мы можем просто использовать оба режима вместе:

Режим пересылки: вычисление произведения вектора градиента ?F Vустановив ? = v.
Режим реверса: возьмите результат и примените к нему обратное распространение: ??fv = Hv

Умный, верно? Затем гессиан может быть использован для оптимизации высшего порядка, которая также учитывает приблизительную кривизну поверхности потерь. В заключение: еще есть некоторая любовь к прямому режиму AD.

Мы видели мощность и ограничения автоматического дифференцирования в прямом режиме. Это позволяет нам оценивать функцию и ее производную одновременно Таким образом, можно преодолеть двухфазную доктрину обратного режима AD, известного как backprop. Это происходит за счет хранения двойных представлений всех промежуточных узлов. Кроме того, вычислительное усилие отдельного обратного прохода переносится на прямой проход. Мы увидели, как магические алгебраические свойства двойных чисел позволяют нам делать это эффективно и точно.

В общем, я нашел, что это чрезвычайно приятно, а также очень проницательно, чтобы реализовать вещи с нуля. Я совершенно по-другому отношусь к текущим библиотекам DL, а также к их проблемам (например, статические и динамические вычислительные графы, хранилище и вычисления). Я рекомендую заинтересованному читателю поближе познакомиться с большим обзором Baydin et al. (2018). Эта статья стала моей отправной точкой и дает очень читаемый обзор! Также вы можете найти весь кодВот,

В основном эта операция применяется для исследования функций, а также величин, изменяющихся с течением времени.

В этом случае необходимо знать правила дифференцирования. Это довольно простая задача, когда функция соответствует табличному значению.

Однако бывают случаи, когда она является сложной.

Общая информация

Нахождение производной (дифференцирование) функции является одной из важнейших математических операций. Это позволяет существенно сократить объем вычислений. Например, при исследовании какой-либо функции, необходимо найти ее область значения. Существует множество методов решения данной задачи, но только нахождение производной позволяет оптимизировать вычисления. В данном случае к оптимизации относится экономия времени и сокращение объемов вычислений.

Дифференцирование применяется не только в математике, но и в некоторых других сферах человеческой жизни. Это прежде всего объясняется количеством затраченного времени и простотой расчетов.

Сферы использования

В физике с ее помощью можно найти такие величины: силу, ускорение, мощность, массу тонкого физического тела (стержня), скорость, теплоемкость, мгновенные значения тока и напряжения, а также другие величины. Последние должны изменяться с течением времени или по какому-либо закону. Если величина является постоянной (константой), то ее производная равна 0.

В химии и фармацевтике операция дифференцирования получила также широкое применение. Ее следует применять для точного расчета массы или массовой доли реактивов. Кроме того, она позволяет найти оптимальную дозу лекарственного препарата, при которой эффект будет максимальным, а побочные действия — минимальными.

Агропромышленный комплекс тоже нуждается в выполнении данной операции. Например, для определения оптимальности соотношения сторон земельных участков. В современных экономических исследованиях применяются определенные математические функции. Для их исследования необходимы знания в области дифференцирования.

Для анализа нужно применять алгоритм, позволяющий существенно уменьшить затраченное время. Для этих целей специалисты рекомендуют применять дифференцирование.

Понятие производной

Производная некоторой функции является дифференциальным исчислением, которое характеризует ее скоростное изменение в искомой точке. Более сложное определение: предел отношения приращения функции к приращению ее аргумента с тем условием, что последнее стремится к 0. Главное условие — предел должен существовать. Если его нет, то функция не меняется и является константой. В этом случае говорят, что производной не существует, поскольку она равна 0.

Функция, которая имеет производную в определенной точке, называют дифференцируемой в этой точке. Процесс нахождения производной является дифференцированием. Обратная операция по нахождению первообразной — интегрированием. Она имеет два смысла: геометрический и физический.

К первому следует отнести тангенс угла наклона касательной прямой к некоторому графику. Сначала выбирается секущая (прямая, пересекающая график в двух и более точках). После этого нужно взять любую точку, полученную при пересечении. Затем, используя точку в качестве оси вращения, изменить плавно положение секущей. В некоторый момент она окажется касательной, т. е. будет иметь только одну точку соприкосновения с графиком.

Физический смысл — скорость изменения функции. Нужно рассмотреть закон движения S = s(t). Выражение является законом, который описывает прямолинейное движение физического тела. Нужно найти мгновенную скорость (V) в момент времени to: V(to) = [s(to)]'. Если взять еще одну производную, то получится величина, называемая ускорением: a(to) = [V(to)]' = [s(to)]''.

Табличные значения

Для нахождения дифференциала какой-либо функции необходимо выполнить некоторые вычисления, которые могут занять время. Специалисты позаботились об экономии времени. Они составили таблицу элементарных функций (рис. 1).

Их и следует применять для решения задач. Если задача является довольно простой, то правила нахождения производной сводятся к элементарным операциям.

Для этого достаточно применить простой алгоритм для чайников:

Выполнить преобразование или упрощение выражения до табличного значения.
Взять производную и записать результат.

Во втором пункте следует руководствоваться табличными значениями. Например, следует продифференцировать степенную функцию вида y = x^3 / 3. Для решения задания необходимо выполнить преобразование — вынести константу: y = (2/3) * x^3. По таблице на рисунке 1 можно найти дифференциал: y' = (2/3) * (x^3)' = (2/3) * 3 * x^2 = 2x^2.

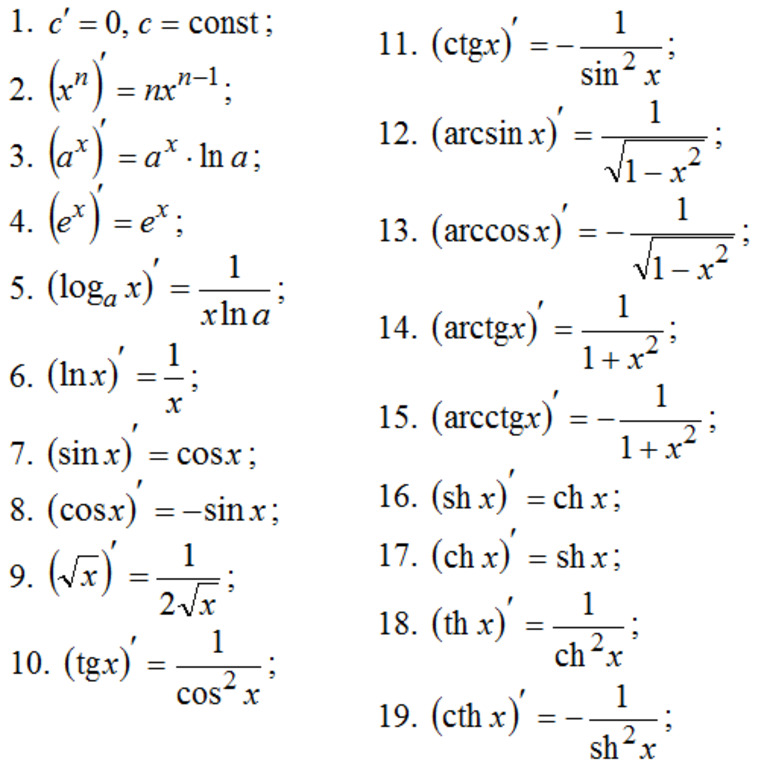
Рисунок 1. Производные простых функций.

Однако не все задачи являются простыми, поскольку существуют сложные функции, для которых необходимо применять правила дифференцирования сложной функции. Кроме того, нужно разобрать основные правила дифференцирования. Их можно применять и для простых выражений.

Правила дифференцирования

Для выполнения операции нахождения производной существуют определенные правила, которые позволяют правильно произвести взятие дифференциала некоторой функции.

Правила — порядок действий, позволяющих исключить неверные решения задач. Они получены в результате доказательств теорем и следствий из них. Первые необходимы для доказательства некоторых утверждений, которые могут заметно облегчить вычисления.

Простым примером является нахождение гипотенузы прямоугольного треугольника (длины катетов известны). Следует воспользоваться теоремой Пифагора. Нет необходимости доказывать, что квадрат гипотенузы равен сумме квадратов катетов, поскольку это забирает время. Существуют такие свойства (правила) дифференциации:

Вынесение константы за знак дифференциала: (C * f(x))' = C(f(x))'.
Если функция представлена в виде суммы (разности) двух функций, то при ее дифференцировании нужно найти производные каждого элемента: (y(x) + z(x))' = y'(x) + z'(x) и (y(x) - z(x))' = y'(x) - z'(x).
Дифференциал умножения функций f(x) и g(x) равен сумме произведений каждой функции на производную другой: (y(x) * z(x))' = (y'(x) * z(x) + y(x) * z'(x).
Производная частного функций y(x) и z(x) равна числителю, который представляет собой разность произведений знаменателя на дифференциал числителя, и производной знаменателя, умноженного на числитель. Кроме того, знаменатель — квадрат знаменателя исходной дроби: (y(x) / z(x))' = [(y'(x) * z(x) - y(x) * z'(x)] / (z(x))^2.

Каждое из правил необходимо применять в конкретной ситуации. Например, если нужно выполнить нахождение дифференциала суммы двух функций, умноженных на константу, то можно воспользоваться двумя правилами.

Алгоритм для сложной функции

Нахождение производной существенно усложняется в том случае, когда функция является сложной. Она состоит из нескольких элементарных выражений. Необходимо находить дифференциал каждой отдельно. Для этой цели пригодятся свойства нахождения производной, каждое из которых следует применять в конкретной ситуации.

Специалисты рекомендуют новичкам воспользоваться некоторым алгоритмом. Он позволяет существенно сократить время и количество вычислений. Решать без алгоритма не рекомендуется, поскольку это можно сделать неверно. Кроме того, необходимо воспользоваться формулами дифференцирования — таблицей производных для их отыскания.

Для сложной функции вида y(g(f(x))) порядок ее дифференцирования следующий:

Разбить функцию на составные части.
Найти производную f(x) и записать ее вначале.
Выполнить дифференцирование g, а затем записать ее после f(x): f'(x) * g'(f(x)).
Взять производную y, после этого умножить ее на результат, полученный в пункте 2: f'(x) * g'(f(x)) * y'(g(f(x))).

Принцип очень прост — следует начинать вычислять производную справа налево по частям.

Например, следует найти дифференциал функции y = (1/2) * sin (2x^2 - 6x).

Для наглядности нужно воспользоваться специальным алгоритмом:

Функция имеет вид y = f(g(x)), и состоит из двух частей: g(x) = 2x^2 - 6x и f(x) = sin(g(x)).
Производная первого элемента: g'(x) = (2x^2 - 6x)' = 4x - 6.
Дифференциал 2 функции: f'(x) = [sin(g(x))]' = cos(g(x)).
Получение результата (можно также упростить выражение при необходимости): y' = [(1/2) * sin (2x^2 - 6x)]' = (1/2) * [sin (2x^2 - 6x)]' = (1/2) * (4x - 6) * cos(2x^2 - 6x) = (2x - 3) * cos(2x^2 - 6x).

При решении задачи было задействовано свойство выноса константы за знак дифференциала. Кроме того, функция g(x) — разность двух выражений, производная которых находится по второму свойству дифференцирования. Функция может содержать в своем составе много элементов, но принцип только один.

Следует обратить внимание на первый пункт алгоритма, поскольку нужно правильно разбивать функцию на элементы. На начальной стадии обучения математики рекомендуют воспользоваться онлайн-калькулятором. Он позволяет получить правильное решение. Его можно сравнить результатом, который получен при решении ручным методом.

Пример решения

Сложность задачи зависит от самой функции. Например, если она является простой, то найти ее дифференциал не составит особой сложности. Для этого необходимо просто воспользоваться таблицей производных. В некоторых случаях следует воспользоваться некоторыми свойствами.

Например, необходимо найти дифференциал функции y = 8 * [(3x^3) + ln(x)] / (x^2). Для решения нужно воспользоваться следующими правилами: вынос константы, поиск производной суммы и частного. Найти дифференциал можно таким образом: y' = [8 * [(3x^3) + ln(x)] / (x^2)]' = 8 * [((3x^3 + ln(x))' * x^2 - (3x^3 + ln(x)) * (x^2)') / (x^2)^2] = 8 * [(x^2 + 1/x) * x^2 - 2x * (3x^3 + ln(x))] / x^4 = 8 * [(x^2(x - 6) + 1 - 2ln(x)) / x^3.

Специалисты не рекомендуют находить производные с помощью специализированного программного обеспечения. Бывают случаи, когда в поле для обработки выражение вводится неверно. При этом дифференциал является ошибочным. Кроме того, иногда бывают программные сбои, которые влекут за собой получение ложного результата. В любом случае нужно уметь дифференцировать функции любой сложности.

Таким образом, для нахождения дифференциала произвольной функции следует знать таблицу производных, основные правила и алгоритмы ее нахождения. Рекомендует проверять результат, полученный при вычислении, при помощи онлайн-калькулятора производных.

Читайте также: