Как сделать объединение корней в тригонометрических уравнениях

Добавил пользователь Валентин П.
Обновлено: 28.08.2024

Вот именно в этой части мы будем с вами искать корни и пожалуйста не ленитесь писать эти пограничной точки не .

Отбор корней тригонометрического уравнения, принадлежащих данному промежутку, с помощью единичной окружности.

Продолжаем решать номер 13 - теперь пункт б, отбор корней, принадлежащих промежутку [. ;. ]. Существует 3 основных .

В 90% случаев отобрать корни удобнее с помощью окружности, но есть и редкие неприятные задачи, поэтому знать .

Мы тут запарились и сделали подробное видео по решению тригонометрических уравнений. Было нелегко уместить .

Математика без Ху%!ни. Егэ, задание С1 Тригонометрическое уравнение. Отбор корней. Просто, доступно и со вкусом .

О самом популярном методе отборе корней в этом видео. На первый взгляд он кажется простым, но лишь пока не появятся .

разбираем сложные задания №13 по тригонометрии - примеры, в которых нужно учитывать ОДЗ ( область допустимых .

Сегодня мы научимся объединять наборы корней в более крупные и простые конструкции, с которыми в дальнейшем .

А вы задумывались когда-нибудь, для чего нужны все эти страшные, на первый взгляд, конструкции из косинусов и синусов .

Решение тригонометрических уравнений из ЕГЭ по математике 2016. Отбор корней на отрезке. Формула понижения .

Часть урока "Тригонометрические уравнения. Выборка корней", проведенного с использованием платформы Maketest в .

В данном уроке рассматривается решение тригонометрического уравнения, которое можно использовать в качестве .

Решаем задачи(упражнения) на заказ (!). P.S. Если хочешь решать задачи и при этом зарабатывать, то напиши нам на .

. вот вы много уравнения тригонометрических порешает вы поймете что это очень простое что нам нужно с вами сделать .

Подготовка к ЕГЭ и ОГЭ. Видеоуроки по всем темам. 3 способа отбора корней в 13 задании. Тригонометрия. Если вы .

Обычно при решении тригонометрических уравнений получаются красивые корни и табличные значения. Но что делать .

Открытый урок в режиме реального времени. Трансляция, во время которой Ольга Александровна будет разбирать вместе .

У тебя были вопросы по этой теме? Я постарался подробно поговорить про арксинусы, арккосинусы и арктангенсы!

В этом уроке Ольга Александровна начнет разбирать тригонометрические выражения. Будет преобразование .

. как у меня есть два корня я это условия для каждого из корней должен расписывать отдельно давайте разделим доску на .

О нас: - Преподаватели из ведущего университета страны - МГУ - Готовим к ЕГЭ с 2018 года - 5000 выпускников - 139 .

В этой статье будут рассмотрены тригонометрические уравнения с корнями. Прежде чем приступить к решению, вспомним, когда появляется опасность потерять корни или приобрести посторонние. Итак:

При решении тригонометрических уравнений могут появиться посторонние корни, если:

1) Уравнение содержит тангенс или котангенс;

2) Обе части уравнения умножаются или делятся на выражение, содержащее неизвестное;

3) Обе части уравнения возводятся в квадрат.

При решении тригонометрических уравнений могут быть потеряны корни, если:

1) Обе части уравнения умножаются или делятся на выражение, содержащее неизвестное;

2) Используются тригонометрические формулы, которые справедливы не при всех значениях неизвестного;

3) При решении системы тригонометрических уравнений для обозначения целого числа в найденных значениях x и y используется только одна буква.

Теперь можно начать решение.

Возводим обе части уравнения в квадрат:

Разложим формулу , и представим единицу как сумму квадрата синуса и квадрата косинуса:

Видим, что в первой скобке – квадрат суммы:

Приравниваем к нулю каждый множитель и решаем два получившихся уравнения:

Первое:

При возведении в квадрат:

Заметим, что по решению синус и косинус равны по модулю, но разные по знаку. В этом варианте решения в исходном уравнении слева под корнем окажется величина отрицательная, значит, это – посторонние корни, поэтому мы даже не будем их записывать. Приобрели мы посторонние корни в результате возведения уравнения квадрат.

Второе:

Возводим в квадрат:

Снова уравнение распалось на два:

– это посторонний корень, который приведет к появлению в исходном уравнении корня из отрицательного числа в правой части.

или n, n in Z" />
– данный корень тоже содержит посторонние корни, которые также приобретены в результате возведения уравнения в квадрат. При синусе, равном нулю, косинус может быть равен как 1, так и (-1). Второе – недопустимо: в этом случае в правой части исходного уравнения – отрицательное число под корнем. Поэтому решение у уравнения всего одно: n, n in Z" />
.

Возводим обе части уравнения в квадрат:

Косинус двойного аргумента заменяем, также от синуса переходим к косинусу с помощью основного тригонометрического тождества:

Корни:

или

Проверка показывает, что все корни удовлетворяют исходному уравнению.

Чтобы избавиться от корня, возведем в квадрат:

Домножим на 2 для удобства:

или

При возведении в квадрат:

Так как правая часть уравнения должна быть неотрицательной, и, кроме того, синус и косинус – разных знаков, то решение одно:

Так как решения уравнения не являются решениями исходного уравнения, то деление на не приведет к потере корней, тогда разделим на :

Решением этого уравнения является угол, синус и косинус которого имеют разные знаки. При этом угол в четвертом квадранте нам не подойдет: у такого угла отрицательный синус и положительный косинус, а это противоречит исходному уравнению: приведет к отрицательному значению операции извлечения корня. Угол во втором квадранте нас устроит.

Ответ: /4+2n" />
, - arctg+2n" />

Сразу делаем вывод, что полученный нами далее в ходе решения должен быть неположительным , иначе результат извлечения корня не будет положительным.

Возводим все уравнение в квадрат, чтобы избавиться от корня:

Раскрываем формулу двойного аргумента и заменяем синусы на косинусы:

Получили квадратное уравнение относительно косинусов:

или – очевидно, что решение второго – пустое множество.

С учетом того, что синус должен быть отрицателен (или равен нулю), решение единственное:

Полученный в ходе решения косинус может быть или отрицательным числом, или нулем.

Возводим уравнение в квадрат:

Формулу тройного аргумента раскроем:

или – сумма коэффициентов уравнения равна 0, поэтому первый корень – 1, а второй – с/a – (-1/2)

Итак, имеем: , или , или

Решения первого уравнения:

Решения второго уравнения:

– не являются решениями исходного уравнения, так как косинус должен быть отрицателен.

Ответ: /2+n, n in Z" />
, >/3+2n, n in Z" />

Замечаем, что синус должен быть неотрицательным числом, так как слева – корень.

Возводим в квадрат:

Раскроем формулу тройного аргумента:

Домножим на 3 для удобства:

Приравняем к нулю оба множителя:

или

Решаем теперь второе, квадратное, уравнение:

Корни получаются такие: 2/3 и (-3/4) – последний корень не подходит по ОДЗ, так как результат извлечения корня не может быть отрицательным.

Второму корню будет соответствовать решение:

n, n in Z" />
и -arcsin (2/3)+2n, n in Z" />
, эти два решения можно объединить в одно и записать: n, n in Z" />

Решение простейших тригонометрических уравнений

Градусы и радианы

Знакомство с тригонометрической окружностью

Повороты на тригонометрической окружности

Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах .

1 радиан = 180/p ? 57,3 градусов

Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа p.

Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на p!

О графиках синуса, косинуса и тангеса поговорим в другой статье.

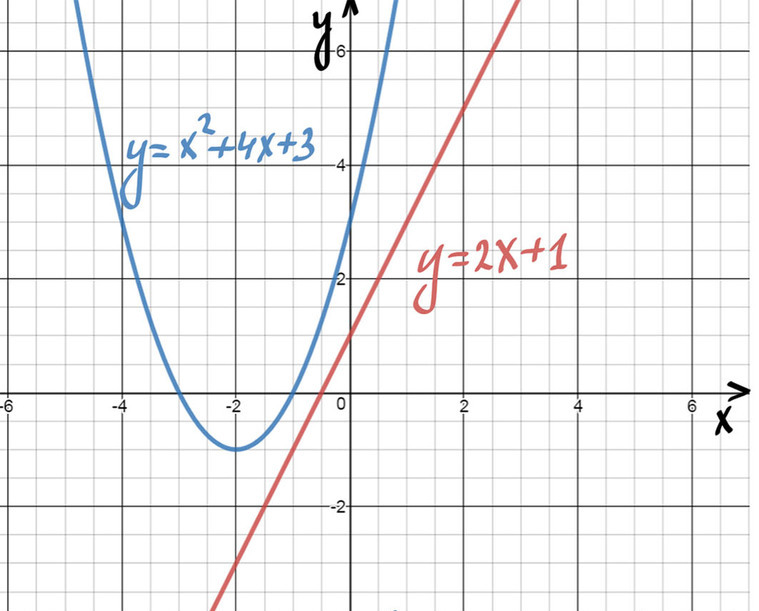
А сейчас начем с декартовой (прямоугольной) системы координат.

Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.

На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:

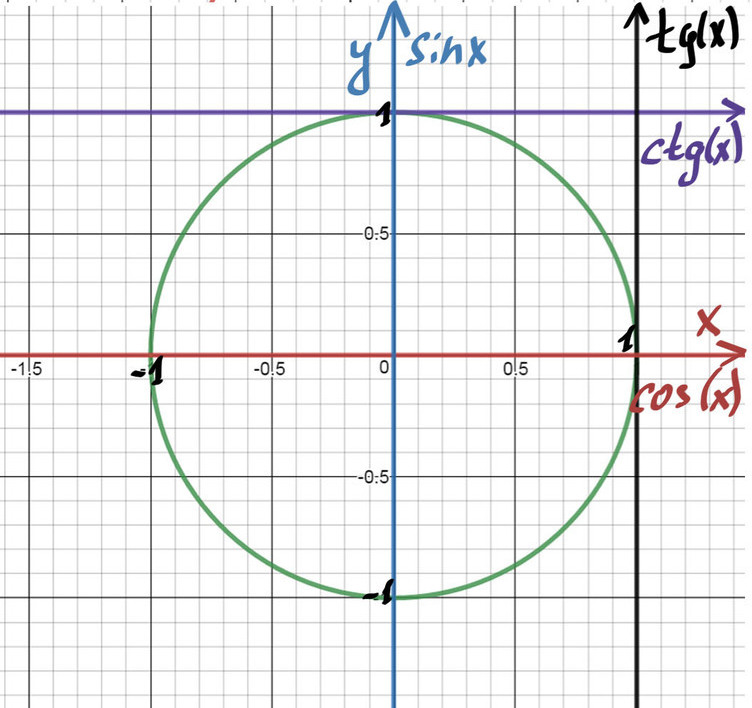
Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.

А теперь отметим основные значения градусов и радиан на окружности.

Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.

Достаточно запомнить, что p = 180° (тогда p/6 = 180/6 = 30°; p/3 = 180/3 = 60°; p/4 = 180/4 = 45°).

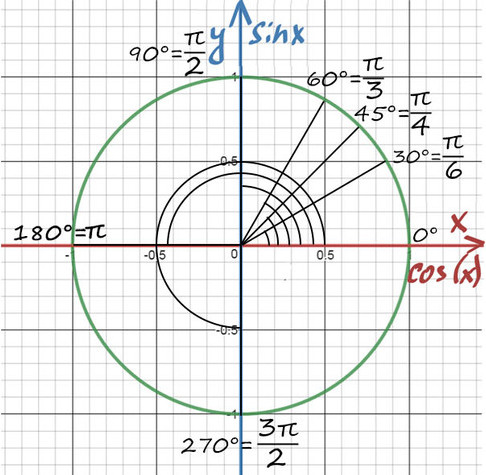
А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):

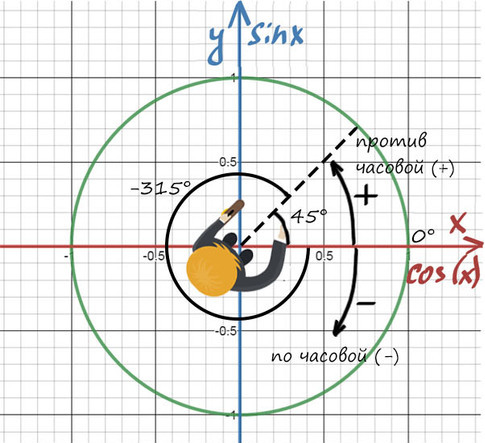
От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).

Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).

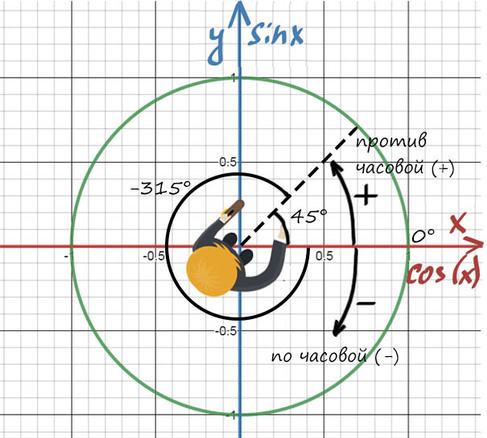
Главное — направление, куда мы будем смотреть, а не угол!

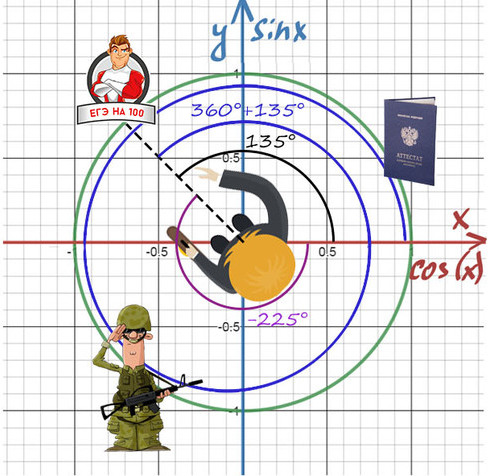
Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°.

А теперь у тебя есть два пути:

Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:

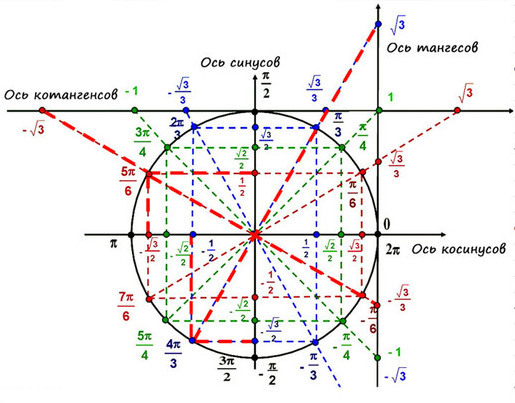
А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.

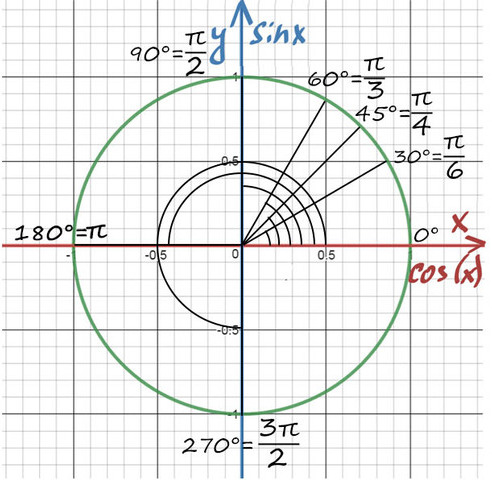
Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.

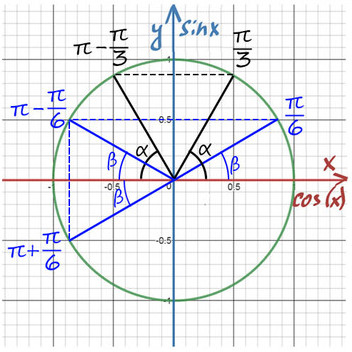
Сразу попробуем разобрать на примере:

1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение 1/2 и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.

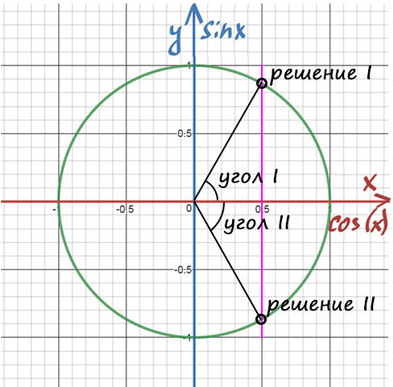
2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.

Дело за малым — найти эти углы.

Или запомнить такой прием:

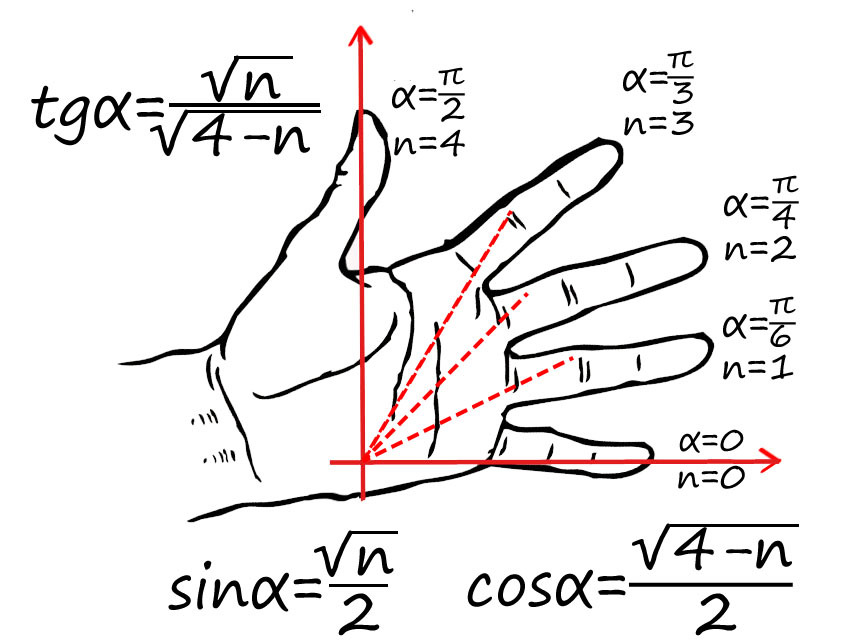
Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).

Например, требуется найти sin(p/2) : p/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(p/2) = ?4/2 = 1 => sin(p/2) = 1.

cos(p/4) - ? p/4 соответсвует среднему пальцу (n = 2) => cos(p/4) = ?2/2.

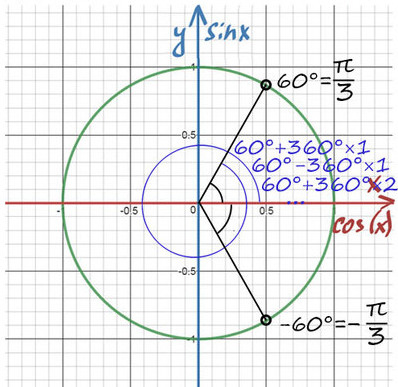
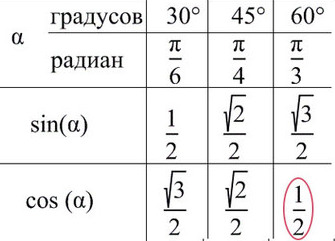
При значении cos(x) = 1/2 из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +p/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).

Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (-). x = -p/3 (угол показан нижней черной дугой).

И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:

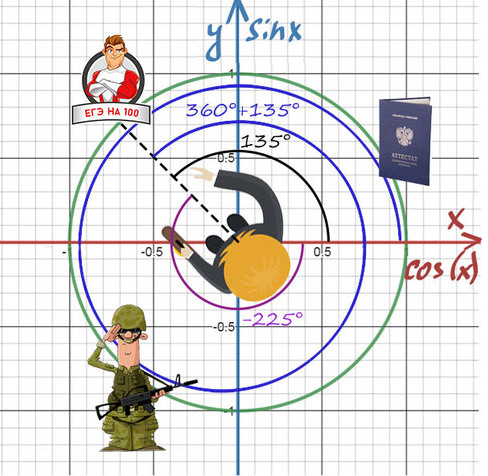
То же самое и здесь! Разные углы могут отражать одно и то же направление.

Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2p (синим цветом) сколько угодно раз и в любом направлении.

Таким образом, попасть в первое направление 60° можно: . 60°-360°, 60°, 60°+360°.

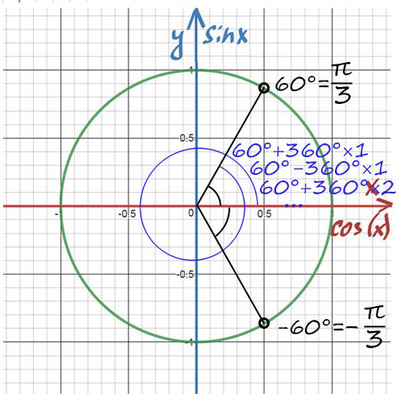
И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть?)

Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n?Z) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = -60 + 360n.

Но мы же договорились, что на окружности все записывают через p, поэтому cos(x) = 1/2 при x = p/3 + 2pn, n?Z и x = -p/3 + 2pk, k?Z.

Ответ: x = p/3 + 2pn, x= - p/3 + 2pk, (n, k) ?Z.

Пример №2. 2sinx = ?2

Первое, что следует сделать, это перенести 2-ку вправо => sinx=?2/2

1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем ?2/2 и проводим ? фиолетовую прямую до пересечений с окружностью.

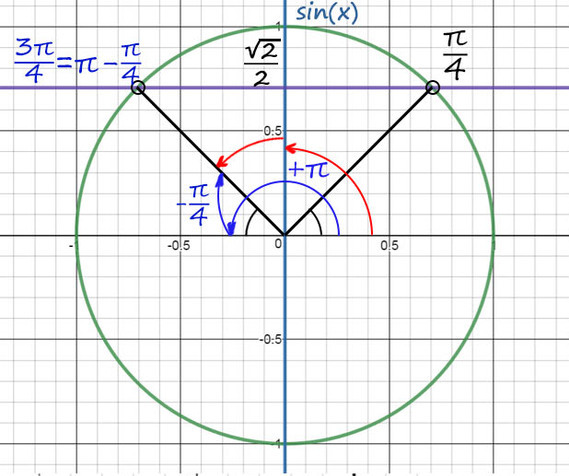
2) Из таблицы sinx = ?2/2 при х = p/4, а вторую точку будем искать с помощью поворота до p, а затем нужно вернуться обратно на p/4.

Поэтому вторая точка будет x = p - p/4 = 3p/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.

И еще не забудем добавить +2pn, n?Z.

Ответ: 3p/4 + 2pn и p/4 + 2pk, k и n - любые целые числа.

Пример №3. tg(x + p/4) = ?3

Вроде все верно, тангенс равняется числу, но смущает p/4 в тангенсе. Тогда сделаем замену: y = x + p/4.

tg(y) = ?3 выглядит уже не так страшно. Вспомним, где ось тангенсов.

1) А теперь на оси тангенсов отметим значение ?3, это выше чем 1.

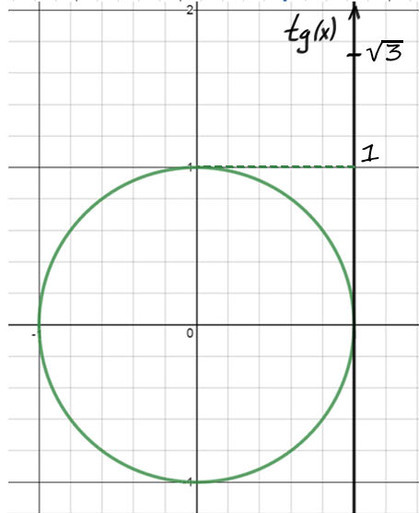
2) Проведем фиолетовую прямую через значение ?3 и начало координат. Опять на пересечении с окружностью получается 2 точки.

По мнемоническому правилу при тангенсе ?3 первое значение — это p/3.

3) Чтобы попасть во вторую точку, можно к первой точке (p/3) прибавить p => y = p/3 + p = 4p/3.

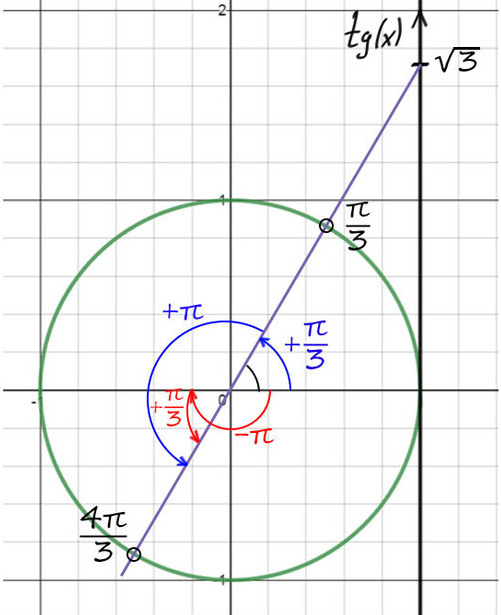
4) Но мы нашли только y , вернемся к х. y = p/3 + 2pn и y = x + p/4, тогда x + p/4 = p/3 + 2pn => x = p/12 + 2pn, n?Z.

Второй корень: y = 4p/3 + 2pk и y = x + p/4, тогда x + p/4 = 4p/3 + 2pk => x = 13p/12 + 2pk, k?Z.

Теперь корни на окружности будут здесь:

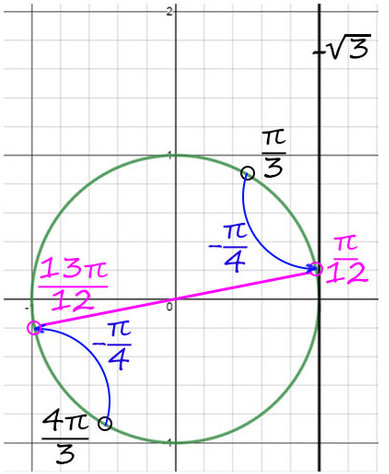
Ответ: p/12 + 2pn и 13p/12 + 2pk, k и n — любые целые числа.

Конечно, эти два ответа можно объединить в один. От 0 поворот на p/12, а дальше каждый корень будет повторяться через каждый p (180°).

Ответ можно записать и так: p/12 + pn, n?Z.

Пример №4: -10ctg(x) = 10

Перенесем (-10) в другую часть: ctg(x) = -1. Отметим значение -1 на оси котангенсов.

1) Проведем прямую через эту точку и начало координат.

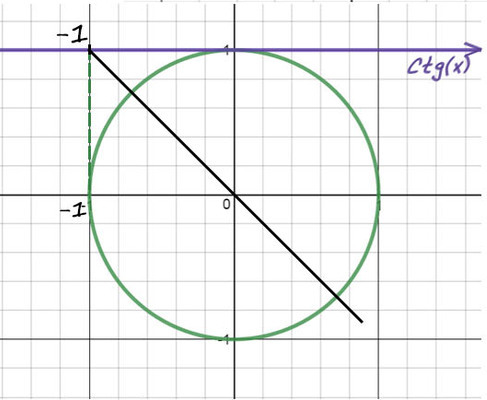
2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при p/4). Но здесь -1, поэтому одна точка будет -p/4. А вторую найдем поворотом до p, а потом назад на p/4 (p - p/4).

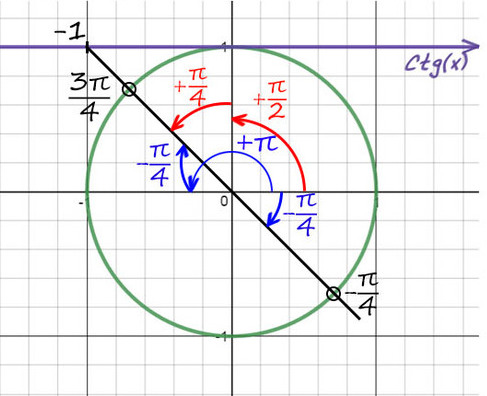
Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (p, 2p, 3p. ) так намного меньше шансов запутаться.

Не забываем добавить к каждой точке 2pk.

Ответ: 3p/4 + 2pn и -p/4 + 2pk, k и n — любые целые числа.

Алгоритм решения тригонометрических уравнений (на примере cos(x) = - ? 3/2) :

При решении тригонометрических уравнений могут появиться посторонние корни, если:

1) Уравнение содержит тангенс или котангенс;

2) Обе части уравнения умножаются или делятся на выражение, содержащее неизвестное;

3) Обе части уравнения возводятся в квадрат.

При решении тригонометрических уравнений могут быть потеряны корни, если:

1) Обе части уравнения умножаются или делятся на выражение, содержащее неизвестное;

2) Используются тригонометрические формулы, которые справедливы не при всех значениях неизвестного;

Теперь можно начать решение.

Возводим обе части уравнения в квадрат:

Разложим формулу , и представим единицу как сумму квадрата синуса и квадрата косинуса:

Видим, что в первой скобке – квадрат суммы:

Приравниваем к нулю каждый множитель и решаем два получившихся уравнения:

Первое:

При возведении в квадрат:

Второе:

Возводим в квадрат:

Снова уравнение распалось на два:

Возводим обе части уравнения в квадрат:

Корни:

или

Проверка показывает, что все корни удовлетворяют исходному уравнению.

Чтобы избавиться от корня, возведем в квадрат:

Домножим на 2 для удобства:

или

При возведении в квадрат:

Ответ: /4+2n" />
, - arctg+2n" />

Возводим все уравнение в квадрат, чтобы избавиться от корня:

Раскрываем формулу двойного аргумента и заменяем синусы на косинусы:

Получили квадратное уравнение относительно косинусов:

или – очевидно, что решение второго – пустое множество.

С учетом того, что синус должен быть отрицателен (или равен нулю), решение единственное:

Полученный в ходе решения косинус может быть или отрицательным числом, или нулем.

Возводим уравнение в квадрат:

Формулу тройного аргумента раскроем:

или – сумма коэффициентов уравнения равна 0, поэтому первый корень – 1, а второй – с/a – (-1/2)

Итак, имеем: , или , или

Решения первого уравнения:

Решения второго уравнения:

– не являются решениями исходного уравнения, так как косинус должен быть отрицателен.

Ответ: /2+n, n in Z" />
, >/3+2n, n in Z" />

Замечаем, что синус должен быть неотрицательным числом, так как слева – корень.

Возводим в квадрат:

Раскроем формулу тройного аргумента:

Домножим на 3 для удобства:

Приравняем к нулю оба множителя:

или

Решаем теперь второе, квадратное, уравнение:

Второму корню будет соответствовать решение:

n, n in Z" />
и -arcsin (2/3)+2n, n in Z" />
, эти два решения можно объединить в одно и записать: n, n in Z" />

Читайте также: