Как сделать логическую операцию
Добавил пользователь Skiper Обновлено: 10.09.2024
В данной публикации мы рассмотрим 5 логических операций: приведем их определения, способы записи (если он есть), а также соответствующие им таблицы истинности.
- Основные термины
- Логические операции и таблицы истинности
- Умножение (конъюнкция)
- Сложение (дизъюкция)
- Отрицание (инверсия)
- Следование (импликация)
- Равнозначность (эквивалентность)
Основные термины
Высказывание – предложение, которое выражает некоторое суждение, по которому определяется, истинно оно (обозначается цифрой “1”) или ложно (пишется как “0”).
Логическая операция – действие в уме, в результате которого меняется содержание или объем понятий, а также, образуются новые понятия.
Логическое выражение – устное или письменное утверждение, в котором присутствуют как постоянные величины, так и переменны. В зависимости от принимаемых переменными значений, логическое выражение может быть либо истинным (1), либо ложным (0).
Сложное логическое выражение – это составное выражение, которое включает одно или несколько простых и/или сложных логических выражений, связанных между собой логическими операциями.
Логические операции и таблицы истинности
Умножение (конъюнкция)
Конъюкция – это сложное логическое выражение, являющееся истинным исключительное в том случае, если оба простых выражения, из которых оно состоит, являются истинными. В противном случае, оно ложно.
Прежде всего, начнем с разбора названия самого предмета, а именно выясним, каково значение алгебры, логики, а затем алгебры логики.
Алгебра – это раздел математики, предназначенный для описания действий над переменными величинами, которые принято обозначать строчными буквами латинского алфавита – а, b, x, y и т.д. Действия над переменными величинами записываются в виде математических выражений.
Алгеброй логики называется аппарат, который позволяет выполнять действия над высказываниями.
Алгебру логику называют также алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения. В булевой алгебре высказывания принято обозначать прописными латинскими буквами: A, B, X, Y. В алгебре Буля введены три основные логические операции с высказываниями: Сложение, умножение, отрицание. Определены аксиомы (законы) алгебры логики для выполнения этих операций. Действия, которые производятся над высказываниями, записываются в виде логических выражений.
Логические выражения могут быть простыми и сложными.
Сложное логическое выражение содержит высказывания, объединенные логическими операциями. По аналогии с понятием функции в алгебре сложное логическое выражение содержит аргументы, которыми являются высказывания.
В качестве основных логических операций в сложных логических выражениях используются следующие:
• НЕ (логическое отрицание, инверсия);
• ИЛИ (логическое сложение, дизъюнкция);
• И (логическое умножение, конъюнкция).
Логическое отрицание является одноместной операцией, так как в ней участвует одно высказывание. Логическое сложение и умножение — двуместные операции, в них участвует два высказывания. Существуют и другие операции, например операции следования и эквивалентности, правило работы которых можно вывести на основании основных операций.
Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении, например:
Операция НЕ — логическое отрицание (инверсия)
Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее:
• если исходное выражение истинно, то результат его отрицания будет ложным;
• если исходное выражение ложно, то результат его отрицания будет истинным.
Для операции отрицания НЕ приняты следующие условные обозначения:
Результат операции отрицания НЕ определяется следующей таблицей истинности:
A не А 0 1 1 0 Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот.
Приведем примеры отрицания.
2. Высказывание «Уравнение у = 4х + 3 в промежутке -2
Принцип работы переключателя настольной лампы таков: если лампа горела, переключатель выключает ее, если лампа не горела — включает ее. Такой переключатель можно считать электрическим аналогом операции отрицания.
Операция ИЛИ — логическое сложение (дизъюнкция, объединение)
Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами. Результатом операции ИЛИ является выражение, которое будет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений.
Применяемые обозначения: А или В, А V В, A or B.
Результат операции ИЛИ определяется следующей таблицей истинности:
A B А или B 0 0 0 0 1 1 1 0 1 1 1 1 Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложен тогда, когда аргументы А и В — ложны.
Приведем примеры логического сложения.
Кто хоть однажды использовал елочную гирлянду с параллельным соединением лампочек, знает, что гирлянда будет светить до тех пор, пока цела хотя бы одна лампочка. Логическая операция ИЛИ чрезвычайно схожа с работой подобной гирлянды, ведь результат операции ложь только в одном случае — когда все аргументы ложны.
Операция И — логическое умножение (конъюнкция)
Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.
Применяемые обозначения: А и В, А ? В, A & B, A and B.
Результат операции И определяется следующей таблицей истинности:
A B А и B 0 0 0 0 1 0 1 0 0 1 1 1 Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.
Приведем примеры логического умножения.
Логическую операцию И можно сравнить с последовательным соединением лампочек в гирлянде. При наличии хотя бы одной неработающей лампочки электрическая цепь оказывается разомкнутой, то есть гирлянда не работает. Ток протекает только при одном условии — все составляющие цепи должны быть исправны.
Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.
если А, то В; А влечет В; if A then В; А-> В.
A B А -> B 0 0 1 0 1 1 1 0 0 1 1 1 Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.
Приведем примеры операции следования.
c) А — истинно, В — ложно (3-я строка таблицы истинности). Невозможно найти такие числа, которые делились бы на 9, но не делились на 3. Истинная предпосылка не может приводить к ложному результату импликации.
Применяемое обозначение: А = В, А ~ В.
A B А~B 0 0 1 0 1 0 1 0 0 1 1 1 Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.
Приведем примеры операции эквивалентности:
1. День сменяет ночь тогда и только тогда, когда солнце скрывается за горизонтом;
2. Добиться результата в спорте можно тогда и только тогда, когда приложено максимум усилий.
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение — составные высказывания в виде формулы.
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице по формуле m=2 n , где n — количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
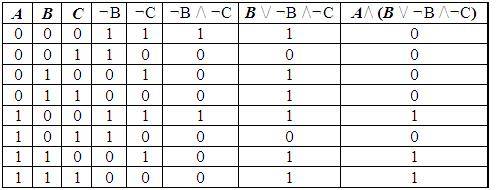
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 2 3 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
![Логические выражения и таблица истинности]()
Пример 2. Определите истинность логического выражения F(А, В) = (А\/ В)/\(¬А\/¬В) .
Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.
Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истина, ложь). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных соотношениях.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Логических значений всего два: истина (TRUE) и ложь (FALSE). Это соответствует цифровому представлению — 1 и 0. Результаты каждой логической операции можно записать в виде таблицы. Такие таблицы называют таблицами истинности.
Основные операции алгебры логики
Операция, используемая относительно одной величины, называется унарной. Таблица значений данной операции имеет вид
A ¬A истина ложь ложь истина A ¬A 1 0 0 1 Высказывание $A?$ ложно, когда А истинно, и истинно, когда А ложно.
Геометрически отрицание можно представить следующим образом: если А — это некоторое множество точек, то $A?$ — это дополнение множества А, т. е. все точки, которые не принадлежат множеству А.
![]()
Таблица истинности операции имеет вид
A B A ? B истина ложь ложь ложь истина ложь ложь ложь ложь истина истина истина A B A ? B 1 0 0 0 1 0 0 0 0 1 1 1 Высказывание А ? В истинно только тогда, когда оба высказывания — А и В истинны.
Геометрически конъюнкцию можно представить следующим образом: если А, В — это некоторые множества точек, то А ? В есть пересечение множеств А и В.
![]()
Таблица истинности операции имеет вид
A B A ? B истина ложь истина ложь истина истина ложь ложь ложь истина истина истина A B A ? B 1 0 1 0 1 1 0 0 0 1 1 1 Высказывание А ? В ложно только тогда, когда оба высказывания — А и В ложны.
Геометрически логическое сложение можно представить следующим образом: если А, В — это некоторые множества точек, то А ? В — это объединение множеств А и В, т. е. фигура, объединяющая и квадрат, и круг.
![]()
Таблица истинности операции имеет вид
А В А ? B истина ложь истина ложь истина истина ложь ложь ложь истина истина ложь А В А ? B 1 0 1 0 1 1 0 0 0 1 1 0 Высказывание А ? В истинно только тогда, когда высказывания А и В имеют различные значения.
Таблица истинности операции имеет вид
А В А -> В истина ложь ложь ложь истина истина ложь ложь истина истина истина истина А В А -> В 1 0 0 0 1 1 0 0 1 1 1 1 Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина.
Таблица истинности операции эквивалентности имеет вид
А В А ~ В истина ложь ложь ложь истина ложь ложь ложь истина истина истина истина А В А ~ В 1 0 0 0 1 0 0 0 1 1 1 1 Зная значения простых высказываний, можно на основании таблиц истинности определить значения сложных высказываний. При этом важно знать, что для представления любой функции алгебры логики достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
Сложение по модулю два А ? В $(A? ?B) ? (A ? B?)$ Импликация А -> В $A? ? B$ Эквивалентность А ~ В $(A? ? B?) ? (A ? B)$ Примеры решения задач
Пример 1. Определить для указанных значений X значение логического высказывания ((X > 3) ? (X 3) ? (1 3) ? (12 3) ? (3 2) -> (X > 5)) .
Пример 3. Для каких из приведенных слов ложно высказывание ¬(первая буква гласная ? третья буква гласная) <=> строка из 4 символов? 1) асса; 2) куку; 3) кукуруза; 4) ошибка; 5) силач.
Решение. Рассмотрим последовательно все предложенные слова:
1) для слова асса получим: ¬(1 ? 0) <=> 1, 1 <=> 1 — высказывание истинно;
2) для слова куку получим: ¬ (0 ? 0) <=> 1, 1 <=> 1 — высказывание истинно;
3) для слова кукуруза получим: ¬ (0 ? 0) <=> 0, 1 <=> 0 — высказывание ложно;
4) для слова ошибка получим: ¬ (1 ? 1) <=> 0, 0 <=> 0 — высказывание истинно;
5) для слова силач получим: ¬ (0 ? 0) <=> 1, 1 <=> 0 — высказывание ложно.
Логические выражения и их преобразование
Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения действий следующий:
- вычисление существующих функциональных зависимостей;
- выполнение алгебраических операций (вначале умножение и деление, затем вычитание и сложение);
- выполнение операций сравнения (в произвольном порядке);
- выполнение логических операций (вначале операции отрицания, затем операции логического умножения, логического сложения, последними выполняются операции импликации и эквивалентности).
В логическом выражении могут использоваться скобки, которые изменяют порядок выполнения операций.
Пример. Найти значение выражения:
$1 <= a ? A ? sin(p/a - p/b) a + b ? A ? B)$ для а = 2, b = 3, A = истина, В = ложь.
Решение. Порядок подсчета значений:
1) b a + a b > a + b, после подстановки получим: 3 2 + 2 3 > 2 + 3, т. е. 17 > 2 + 3 = истина;
2) A ? B = истина ? ложь = ложь.
Следовательно, выражение в скобках равно (b a + a b > a + b ? A ? B) = истина ? ложь = истина;
3) 1<= a = 1 <= 2 = истина;
Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Набор логических элементов, состоящий из элементов НЕ, ИЛИ, И, с помощью которых можно построить логическую структуру любой сложности, называется функционально полным.
Построение таблиц истинности логических выражений
Для логической формулы всегда можно записать таблицу истинности, т. е. представить заданную логическую функцию в табличном виде. В этом случае таблица должна содержать все возможные комбинации аргументов функции (формулы) и соответствующие значения функции (результаты формулы на заданном наборе значений).
Удобной формой записи при нахождении значений функции является таблица, содержащая, кроме значений переменных и значений функции, также значения промежуточных вычислений. Рассмотрим пример построения таблицы истинности для формулы $? ? X2 ? ? ? X1$.
X1 X2 $?$ $?$ \ X2 X1 ? X2 $?$ $?$ ? X2 ? $?$ $?$ ? X2 ? $?$ ? X1 1 1 0 0 1 0 0 1 1 0 0 0 1 0 0 1 0 1 1 1 1 0 1 1 0 0 1 0 0 1 1 1 Если функция принимает значение 1 при всех наборах значений переменных, она является тождественно-истинной; если при всех наборах входных значений функция принимает значение 0, она является тождественно-ложной; если набор выходных значений содержит как 0, так и 1, функция называется выполнимой. Приведенный выше пример является примером тождественно-истинной функции.
Зная аналитическую форму логической функции, всегда можно перейти к табличной форме логических функций. С помощью заданной таблицы истинности можно решить обратную задачу, а именно: для заданной таблицы построить аналитическую формулу логической функции. Различают две формы построения аналитической зависимости логической функции по таблично заданной функции.
1. Дизъюнктивно нормальная форма (ДНФ) — сумма произведений, образованных из переменных и их отрицаний для ложных значений.
Алгоритм построения ДНФ следующий:
Пример. Построить функцию, определяющую, что первое число равно второму, используя метод ДНФ. Таблица истинности функции имеет вид
X1 X2 F(X1, X2) 1 1 1 0 1 0 1 0 0 0 0 1 Решение. Выбираем наборы значений аргументов, в которых функция равна 1. Это первая и четвертая строки таблицы (строку заголовка при нумерации не учитываем).
Записываем логические произведения аргументов этих наборов, объединив их логической суммой: X1 ? X2 ? X1 ? X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих ложное значение (четвертая строка таблицы; второй набор в формуле; первый и второй элементы): X1 ? X2 ? $?$ ? $?$.
2. Конъюнктивно нормальная форма (КНФ) — произведение сумм, образованных из переменных и их отрицаний для истинных значений.
Алгоритм построения КНФ следующий:
Примеры решения задач
Пример 1. Рассмотрим предыдущий пример, т. е. построим функцию, определяющую, что первое число равно второму, используя метод КНФ. Для заданной функции ее таблица истинности имеет вид
X1 X2 F(X1, X2) 1 1 1 0 1 0 1 0 0 0 0 1 Решение. Выбираем наборы значений аргументов, в которых функция равна 0. Это вторая и третья строки (строку заголовка при нумерации не учитываем).
Записываем логические суммы аргументов этих наборов, объединив их логическим произведением: X1 ? X2 ? X1 ? X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих истинное значение (вторая строка таблицы, первый набор формулы, второй элемент; для третьей строки, а это второй набор формулы, первый элемент): X1 ? $?$ ? $?$ ? X2.
Таким образом, получена запись логической функции в КНФ.
Полученные двумя методами значения функций являются эквивалентными. Для доказательства этого утверждения используем правила логики: F(X1, X2) = X1 ? $?$ ? $?$ ? X2 = X1 ? $?$ ? X1 ? X2 ? $?$ ? $?$ ? $?$ ? X2 = 0 ? X1 ? X2 ? $?$ ? $?$ ? 0 = X1 ? X2 ? $?$ ? $?$.
Пример 2. Построить логическую функцию для заданной таблицы истинности:
X1 X2 F(X1, X2) 1 1 1 1 0 0 0 1 1 0 0 0 Решение. Используем алгоритм ДНФ для построения исходной функции:
X1 X2 F(X1, X2) 1 1 1 • X1 ? X2 1 0 0 0 1 1 • $?$ ? X2 0 0 0 Искомая формула: X1 ? X2 ? $?$ ? X2 .
Ее можно упростить: X1 ? X2 ? $?$ ? X2 = X2 ? (X1 ? $?$) = X2 ? 1 = X2.
Пример 3. Для приведенной таблицы истинности построить логическую функцию, используя метод ДНФ.
X1 X2 X3 F(X1, X2, X3) 1 1 1 1 • X1 ? X2 ? X3 1 0 1 0 0 1 1 1 • $?$ ? X2 ? X3 0 0 1 0 1 1 0 1 • X1 ? X2 ? $?$ 1 0 0 1 • X1 ? $?$ ? $?$ 0 1 0 0 0 0 0 0 Искомая формула: X1 ? X2 ? X ? $?$ ? X2 ? X3 ? X1 ? X2 ? $?$ ? X1 ? $?$ ? $?$.
Формула достаточно громоздка, и ее следует упростить:
X1 ? X2 ? X3 ? $?$ ? X2 ? X3 ? X1 ? X2 ? $?$ ? X1 ? $?$ ? $?$ = X2 ? X3 ? (X1 ? $?$) ? X1 ? $?$ ? (X2 ? $?$) = X2 ? X3 ? X1 ? $?$.
Таблицы истинности для решения логических задач
Составление таблиц истинности — один из способов решения логических задач. При использовании такого способа решения, условия, которые содержит задача, фиксируются с помощью специально составленных таблиц.
Примеры решения задач
Пример 1. Составить таблицу истинности для охранного устройства, которое использует три датчика и срабатывает при замыкании только двух из них.
X1 X2 X3 Y(X1, X2, X3) 1 1 1 0 1 1 0 1 1 0 1 1 1 0 0 0 0 1 1 1 0 1 0 0 0 0 1 0 0 0 0 0 Пример 2. Составить расписание уроков на день, учитывая, что урок информатики может быть только первым или вторым, урок математики — первым или третьим, а физики — вторым или третьим. Возможно ли составить расписание, удовлетворив всем требованиям? Сколько существует вариантов расписания?
Решение. Задача легко решается, если составить соответствующую таблицу:
1-й урок 2-й урок 3-й урок Информатика 1 1 0 Математика 1 0 1 Физика 0 1 1 Из таблицы видно, что существуют два варианта искомого расписания:
- математика, информатика, физика;
- информатика, физика, математика.
Пример 3. В спортивный лагерь приехали трое друзей — Петр, Борис и Алексей. Каждый из них увлекается двумя видами спорта. Известно, что таких видов спорта шесть: футбол, хоккей, лыжи, плавание, теннис, бадминтон. Также известно, что:
- Борис — самый старший;
- играющий в футбол младше играющего в хоккей;
- играющие в футбол и хоккей и Петр живут в одном доме;
- когда между лыжником и теннисистом возникает ссора, Борис мирит их;
- Петр не умеет играть ни в теннис, ни в бадминтон.
Какими видами спорта увлекается каждый из мальчиков?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как видов спорта шесть, получается, что все мальчики увлекаются разными видами спорта.
Футбол Хоккей Лыжи Плавание Бадминтон Теннис Петр 0 0 1 1 0 0 Борис 0 0 0 Алексей 0 0 Из таблицы видно, что в теннис может играть только Алексей.
Футбол Хоккей Лыжи Плавание Бадминтон Теннис Петр 0 0 1 1 0 0 Борис 0 0 0 0 Алексей 1 0 0 0 0 1 Окончательно получаем, что Борис увлекается хоккеем и бадминтоном. Итоговая таблица будет выглядеть следующим образом:
Футбол Хоккей Лыжи Плавание Бадминтон Теннис Петр 0 0 1 1 0 0 Борис 0 1 0 0 1 0 Алексей 1 0 0 0 0 1 Ответ: Петр увлекается лыжами и плаванием, Борис играет в хоккей и бадминтон, а Алексей занимается футболом и теннисом.

Читайте также:
 webdonsk.ru
webdonsk.ru