Как сделать интерполяцию

Добавил пользователь Alex
Обновлено: 01.09.2024

Обучение переводу статей англоязычной документации, статьи про алгоритмы, а также LifeHacks, статьи по Компьютеру и Программированию, Журнал для Детей, Математику и смежные науки Инженерии.

Поиск по этому блогу

Алгоритмы - Интерполяция. Начальная концепция

Данная стать посвящена алгоритмам интерполяции на примере увеличения и уменьшения изображений. В статье описываются алгоритмы про интерполяцию в общем и интерполяцию на примере изменения размера изображений. Главное выделить смысл заполнения промежутков (включая значащие точки) при увеличении и уменьшении.

1. Введение

Интерполяция — это определение промежутков дискретной функции при потере её значения (к примеру, из-за качества сигнала датчика) или её масштабирование с помощью интерполянтов.

Интерполяция позволяет получить необходимые значения для промежутков или разрывов между значащими точками. Значащие точки — это уже известные точки функции, к примеру, точки изначального изображения, показания с датчиков, имеемые точки функции и т.п.

Не путайте данные методы интерполяции с математеческими методами интерполяции (линейная интерполяция с продолжением, полином Лагранжа, т.п.).

2. Виды интерполяции

В статье приведено несколько видов интерполяции. Это позволит узнать возможности интерполяции на базовом, хотя можно сказать, на продвинутом уровне и придумать более сложные способы интерполяции(интерполянты). Хотя достаточно и этих способов для всех случаев, хотя и не обязательно — решайте сами, но я предлагаю для всего линейную, билёнейную интерполяцию и развитие её смысла для других базисов.

Далее рассматриваются способы интерполяции, приведённые примеры интерполирования решаются системой линейных алгебраических уравнений, подстановкой значащих точек в уравнение интерполянта.

2.1. Интерполяция в одномерном пространстве

Интеполирование в одномерном пространстве представляет нахождение собой значение функции y(t), где известны значащие точки y₁(t₁), y₂(t₂), y₃(t₃), y₄(t₄) и т.д., но нужно найти значение между ними. Значение находится на промежутках [t₁;t₂],[t₂;t₃];[t₃;t₄] и т.д.

2.2. Дублирование до следующего/предыдущего

Смысл этого способа интерполяции заключается в том, что значение функции дублируется до следующего или предыдущего значения, но однозначно для последующих точек.

Далее рассмотрим рисунок этой концепции:

- Значение функции слева

- Значение функции справа

- Восстановленное (интерполированное) значение функции

- Восстановленное (интерполированное) значение функции, одно из

- Альтернативное восстановленное (интерполированное) значение функции

- Альтернативное восстановленное (интерполированное) значение функции, одно из

Рис. 1. Концепция Интерполяции способом дублирования значения (для способа дублирования до правого/левого).

2.3. Интерполяция способом дублирования до ближайшего соседа

Смысл этого способа интерполяции заключается в том, что значение функции берётся то, как у ближайшего соседа. Этот вид интерполяции по результату равен 1-ому способу (2.1. Дублирование до следующего).

Интерполяция дублированием до ближайшего соседа

- Значение функции слева

- Значение функции справа

- Восстановленное (интерполированное) значение функции

- Восстановленное (интерполированное) значение функции, одно из

Рис. 2. Концепция Интерполяции способом дублирования до ближайшего соседа.

2.4. Линейная интерполяция

Смысл этого способа интерполяции заключается в том, что значение функции берётся линией, соединяющей две точки.

Значение левой точки

Значение правой точки

Viewer does not support full SVG 1.1

Рис. 3.1. Концепция Линейной интерполяции.

- Значение функции слева

- Значение функции справа

- Восстановленное (интерполированное) значение функции

- Восстановленное (интерполированное) значение функции, одно из

Рис. 3.2. Концепция Линейной интерполяции.

2.5. Квадратическая интерполяция

Смысл интерполяции заключается в том, что значения точек соединяются кривыми второго порядка (квадратичными или они также называются параболами).

Квадратичная кривая проходит через три точки, которые не являются корнями уравнения параболы, но она через них проходит не симметрично. Парабола геометрически однозначно задаётся тремя точками. Просьба не путать с корнями параболы, корня у параболы максимум два, и они означают координаты точек(и) пересечения с осью абсцисс. Попробуйте написовать параболы и вы увидите, что через три случайные точки однозначно проходит только одна парабола и интервалы не одинаковы.

Viewer does not support full SVG 1.1

Рис. 4. Концепция Квадратической интерполяции.

2.6. Кубическая интерполяция

Интерполяция заключается в том, чтобы провести кубическую кривую, через 4 точки.

Viewer does not support full SVG 1.1

Рис. 5. Концепция Кубической интерполяции.

2.7. Радиальная интерполяция

На рисунке далее две значащие точки соединяются кругом:

Значение левой точки

Значение правой точки

Viewer does not support full SVG 1.1

Рис. 6.1. Концепция Радиальной интерполяции.

На Рис. 6.1. показана концепция Радиальной интерполяции, если между точками равные промежутки. Представьте себе уровни значений значащих точек на круге: если считать, что между точками не равные промежутки, а они просто должны попадать на круг последовательно, то можно интерполировать сразу три значащие точки:

Viewer does not support full SVG 1.1

Рис. 6.2. Концепция Радиальной интерполяции.

Это свойство можно использовать для всех интерполянтов и оно представлено на всех примерах инетрполянтов выше и ниже.

2.8. Эллиптическая интерполяция

Эллиптическая интерполяция производится по аналогии с радиальной, но кривой берётся эллипс.

7VpRd6I4FP41PtZDEgjwWLWd7p7Z057pdqadt1SisEWwSKudX79BAiYhVlCwdc74gMmFXMLNl+/e3KSHhrPVl4TM/X9ij4Y9aHirHhr1IATAsdhfJnnLJZbj5IJpEnj8oY3gNvhFudDg0pfAowvpwTSOwzSYy8JxHEV0nEoykiTxUn5sEofyW+dkSiuC2zEJq9IfgZf6xXdhd3PjigZTn7/agXZ+Y0aKh/mXLHzixUtBhC56aJjEcZqXZqshDTPjFXbJ211uuVt2LKFRWqfB1d+3q1/X84cgvUyW14u/Zt+CmzOu5ZWEL/yDeWfTt8ICSfwSeTRTYvTQYOkHKb2dk3F2d8nGnMn8dBayGmDFaqeKN9AkpStBxDv5hcYzmiZv7BF+FxrcYBwxoDDgcmN/C3OZL5jedLiQ8DGflro3ZmEFbpkGVkItW2mRJvETHcZhnKxbI3f9a8l+ULZfaU/RflBjP9SG/Zam5f839fDdv/fP4etF+HxHvp0BZ7cBmRo2p+lRIIYsxURW1URIBzFgtmCin8/XP/2vK+iT16ebaWw4yLo6MzuFWBRHtDRdxU4aa241HTZ2mw7o0AUw6lsdzU9o1cBX5J1n/oDVYvacbC328cnbPbfsuvKQVViHeXW0Em+O3sqadxmEss0LN4GYZMJuCtN8MqF4PNYRgGe7j4bxHrqpJzmq6gCJ01tj/0KW0JCkwavs3nQjwt9wEwesJxt2MRV2VmfEIn5JxpS3Et2RqgjsUJSSZErTiqI1QMrPPgAz+GDMNBp7j1Bnoh17PHbo4+QAFJ4cZlRHszdmVEVdY8ZthBnOuhVWLlCSSSZxlPKoF1oiBkBDJloF6b1QFlqx2qZRVjkZ3ChuGlhuH1vu5mfvCSO7md6OUYVgFVVsfFgv2HUwWl+NHgOEk0ssQe5wCfO4WWFbk7zsFk1YmTXBIRuuwWPCStOstJavXz24qLzuvAJ0FkOkNWIOkQa5iITBNGLVkE4yDVk8ErAV1zkXzwLPC7cFgnIQFJJHGg7I+Gm6lquvFuaW2VJw7ajQ0USOuikBu1qbFNzaESeZfzhJ4g6srK4A3tOXYdUpqoo6Zh1Ts/TPWCenB8AnPScDdh0K5Z18o6Wo1vljzDBCkxNjEFxxapoFlHFUBrH3YRCPLPy1FYE8iJn8hqRsYKK1BBqoQjLwPZIReOVBopUdJFMSy0PBVCdLMpaKEXdPkqkoQp2RzHDpX33/eoHO8fJ1cfcdRsnk9gzUcE7ZxJvXn1hlqpc8FhoM/VgVLhu5fVcM7mzJJOXiRBha0zH6hvCD1ZFGqiVbm466ZBlD7XnOpgPhmjPrpRC3OTIHK0SeM/Tlb8rE7wOwNj8DZXFQRnwiP5tH5ecDAzxdGPY+P+oDPrCDiRsOyUdzrTr/m3LrFpLYprZrpm3mxD9hCtQYGe5JpEDVFHglfWDu6ax3pSXMrhCl3bRplh/9TLTzueCixh8YS6Nc2bWsCxdbWYlWFHWMD1BjV/RzM86fTZcON130mGkWy3wYZrBBXOZRNZiBIxufJmYyb4Jbgo1GV9fIqbH10tYG+WFnCxDoF/vRRSyoOcGCgNO3rerol6mf1g9hFJ041oZnDd4Vcj7IgvKMdh24c06z2g1NAmafbPHZKBqARg7Y9yDnfOT8NW27L8No70jBVFIeSE0ndTx3oSbV3Ax5ZY7Prp/k63J/vo9dFa54twv6neGqLor2Bquq6OhgPfwsUUu4QyhLK8i4Y1IFd9BtFXc1YfZpwhwTme3gzjKUdZnqiNvDnfYA4MEc2XqE2xnsKtxW4/jhcdCkHgzdG01MkZQcBDKnATkl0Fpmh1U3B8rzxzfH8tHF/w== " style="background-color: rgb(75,71,75);">

Пусть функция задана набором точек на интервале :

, , (3.1)

Задача интерполяции – найти функцию , принимающую в точках те же значения . Тогда, условие интерполяции:

(3.2)

При этом предполагается, что среди значений нет одинаковых. Точки называют узлами интерполяции.

Если ищется только на отрезке – то это задача интерполяции, а если за пределами первоначального отрезка, то это задача экстраполяции.

Задача нахождения интерполяционной функции имеет много решений, так как через заданные точки можно провести бесконечно много кривых, каждая из которых будет графиком функции, для которой выполнены все условия интерполяции. Для практики важен случай интерполяции функции многочленами:

, (3.3)

При этом искомый полином называется интерполяционным полиномом.

При построении одного многочлена для всего рассматриваемого интервала для нахождения коэффициентов многочлена необходимо решить систему уравнений, построенную на основе полинома (3.3). Данная система содержит уравнение, следовательно, с ее помощью можно определить коэффициент. Поэтому максимальная степень интерполяционного многочлена , и многочлен принимает вид

, (3.4)

3.2. Локальная и глобальная интерполяция

Если задан узел интерполяции, то на этих узлах можно построить один интерполяционный многочлен n-й степени, многочленов первой степени и большой набор многочленов степени меньше n, опирающиеся на некоторые из этих узлов.

Теоретически максимальную точность обеспечивает многочлен более высокой степени. Однако на практике наиболее часто используют многочлены невысоких степеней, во избежание погрешностей расчета коэффициентов при больших степенях многочлена.

Если функция интерполируется на отрезке с помощью единого многочлена для всего отрезка, то такую интерполяцию называют глобальной. В случае локальной интерполяции на каждом интервале строится отдельный интерполяционный полином невысокой степени.

3.3. Кусочно-линейная интерполяция

Простейшим и часто используемым видом локальной интерполяции является линейная (или кусочно-линейная) интерполяция. Она заключается в том, что узловые точки соединяются отрезками прямых (рис.3.1), то есть через каждые две точки и проводится прямая, то есть составляется полином первой степени:

, при (3.5)

Рис. 3.1. Кусочно-линейная интерполяция

Коэффициенты и разные на каждом интервале , и находятся из выполнения условий интерполяции на концах отрезка:

(3.6)

Из системы уравнений (3.6) можно найти коэффициенты:

, (3.7)

При использовании кусочно-линейной интерполяции сначала нужно определить интервал, в который попадает значение x, а затем подставить его в выражение (3.5), используя коэффициенты для данного интервала.

3.4. Кусочно-квадратичная интерполяция

В случае квадратичной интерполяции, для каждых трех узловых точек , , , строится уравнение параболы:

, при (3.8)

Рис.3.2. Кусочно-квадратичная интерполяция

Здесь коэффициенты , и разные на каждом интервале и определяются решением системы уравнений для условия прохождения параболы через три точки:

(3.9)

Из системы уравнений (3.9) можно найти коэффициенты:

(3.10)

3.5. Многочлен Лагранжа

При глобальной интерполяции на всем интервале строится единый многочлен. Одной из форм записи интерполяционного многочлена для глобальной интерполяции является многочлен Лагранжа:

(3.11)

где – базисные многочлены степени n:

(3.12)

То есть многочлен Лагранжа можно записать в виде:

(3.13)

Многочлен удовлетворяет условию . Это условие означает, что многочлен равен нулю при каждом кроме , то есть – корни этого многочлена. Таким образом, степень многочлена равна n и при обращаются в ноль все слагаемые суммы, кроме слагаемого с номером , равного .

Выражение (3.11) применимо как для равноотстоящих, так и для не равноотстоящих узлов. Погрешность интерполяции методом Лагранжа зависит от свойств функции , от расположения узлов интерполяции и точки x. Полином Лагранжа имеет малую погрешность при небольших значениях n (n

Интерполя?ция, интерполи?рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

Многим из тех, кто сталкивается с научными и инженерными расчётами часто приходится оперировать наборами значений, полученных опытным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.

Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.

Содержание

Определения

Рассмотрим систему несовпадающих точек (" width="" height="" />
) из некоторой области . Пусть значения функции известны только в этих точках:

$y_i = f(x_i),\quad i=1,\ldots,N.$

Задача интерполяции состоит в поиске такой функции из заданного класса функций, что

Пример

1. Пусть мы имеем табличную функцию, наподобие описанной ниже, которая для нескольких значений определяет соответствующие значения :


0	0
1	0,8415
2	0,9093
3	0,1411
4	-0,7568
5	-0,9589
6	-0,2794

Интерполяция помогает нам узнать какое значение может иметь такая функция в точке, отличной от указанных (например, при x = 2,5).

2. Найти промежуточное значение (способом линейной интерполяции).

6000	15.5
6378	?
8000	19.2

Способы интерполяции

Интерполяция методом ближайшего соседа

Простейшим способом интерполяции является интерполяция методом ближайшего соседа.

Интерполяция многочленами

На практике чаще всего применяют интерполяцию многочленами. Это связано прежде всего с тем, что многочлены легко вычислять, легко аналитически находить их производные и множество многочленов плотно в пространстве непрерывных функций (теорема Вейерштрасса).

Обратное интерполирование (вычисление x при заданном y)

Интерполяция функции нескольких переменных

Другие способы интерполяции

Смежные концепции

— методы нахождения точек за пределами заданного интервала (продление кривой) — методы построения приближённых кривых

См. также

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое "Интерполяция" в других словарях:

ИНТЕРПОЛЯЦИЯ — 1) способ определять по ряду данных величин какого либо математического выражения промежуточные его величины; так напр., по дальности полета ядра при угле возвышения оси пушечного канала в 1°, 2°, 3°, 4° и т. д. можно определить помощью… … Словарь иностранных слов русского языка

интерполяция — вставка, интерполирование, включение, отыскание Словарь русских синонимов. интерполяция см. вставка Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова. 2 … Словарь синонимов

интерполяция — Вычисление промежуточных значений между двумя известными точками. Например: linear линейная интерполяция exponential экспоненциальная интерполяция Процесс вывода цветного изображения, когда пикселы, относящиеся к области между двумя цветными… … Справочник технического переводчика

Интерполяция — (interpolation) Оценка значения неизвестной величины, находящейся между двумя точками ряда известных величин. Например, зная показатели населения страны, полученные при проведения переписи населения, проводившейся с интервалом в 10 лет, можно… … Словарь бизнес-терминов

Интерполяция — нахождение промежуточных значений некоторой закономерности (функции) по ряду известных ее значений. По английски: Interpolation См. также: Преобразования данных Финансовый словарь Финам … Финансовый словарь

интерполяция — и, ж. interpolation f. < лат. interpolatio изменение; переделка, искажение. 1. Вставка позднейшего происхождения в каком л. тексте, не принадлежащая оригиналу. БАС 1. В древних рукописях много интерполяций, внесенных переписчиками. Уш. 1934. 2 … Исторический словарь галлицизмов русского языка

ИНТЕРПОЛЯЦИЯ — (interpolatio), пополнение эмпйрич. ряда значений какой либо величины недостающими промежуточными значениями ее. Интерполирование может быть произведено тремя способами: математич., графич. и логическим. В основе их лежит общая им гипотеза о том … Большая медицинская энциклопедия

ИНТЕРПОЛЯЦИЯ — (от латинского interpolatio изменение, переделка), отыскание промежуточных значений величины по некоторым известным ее значениям. Например, отыскание значений функции y = f(x) в точках x, лежащих между точками x0 и xn, x0 … Современная энциклопедия

ИНТЕРПОЛЯЦИЯ — (от лат. interpolatio изменение переделка), в математике и статистике отыскание промежуточных значений величины по некоторым известным ее значениям. Напр., отыскание значений функции f(x) в точках x, лежащих между точками xo x1 . xn, по… … Большой Энциклопедический словарь

ИНТЕРПОЛЯЦИЯ — в филологии изменение первоначального текста; вставка переписчиком или переводчиком в текст слов или фраз, отсутствовавших в оригинале … Большой Энциклопедический словарь

Требуется вычислить значение функции в точке x , не совпадающей ни с одним из узлов таблицы. Если эта точка лежит между узлами, то такая задача называется интерполяцией. Если точка x лежит за пределами таблицы, то говорят о задаче экстраполяции.

Очевидно, что коэффициенты с _j можно найти методом наименьших квадратов, положив n = m .

Рассмотрим другие способы решения этой задачи.

Выражение (3.2) – алгебраический полином степени n . Покажем, что он проходит через все точки таблицы при n =2 и n =3.

Выражение (3.2) – интерполяционный полином Лагранжа, проходящий через все точки таблицы. Теперь, чтобы найти значение функции в некоторой точке x * , которой нет в таблице, достаточно подставить эту точку вместо x в формулу (3.2) и считать, что

Конечной разностью функции y= f (x) c шагом D x = h называют функцию D y=f (x+h)-f(x). Это первая конечная разность. Вторая конечная разность D 2 y = D ( D y )=[ f ( x +2 h )- f ( x + h )]-[ f ( x + h )- f ( x )]= f ( x +2 h )-2 f ( x + h )+ f ( x ) и т.д.

Предположим, что функция y = f (x) задана в виде таблицы из четырех точек. Построим для нее таблицу конечных разностей:

Предположим, что шаг в этой таблице – постоянный, то есть

Запишем полином, проходящий через все точки таблицы (а это будет полином степени не выше третьей), в следующем виде:

После подстановки в ( 3.5) значений a_i i=0,1,2,3 и q₁ окончательно получаем:

Запишем общий вид полинома n -й степени:

“ I “ означает, что это первый интерполяционный полином Ньютона. Он удобен для вычислений, когда точка х=х * , в которой нужно вычислить функцию, расположена ближе к началу таблицы.

Если точка х * расположена ближе к концу таблицы, то удобнее пользоваться формулой второго интерполяционного полинома Ньютона:

Результаты применения формул (3.6) и (3.7) – одни и те же, если используются одни и те же узлы таблицы.

Функция y задана в виде таблицы

Требуется найти значение аргумента x * , при котором функция принимает некоторое значение y * .

Задачу можно решить по крайней мере двумя различными способами.

1. а) Строим интерполяционный полином (как правило, ИПЛ) y=L_n( x )

в) Решаем уравнение y * =L_n(x) любым подходящим численным методом (например, методом деления отрезка пополам).

Из рисунка видно, что задача может иметь не единственное решение.

2. а) Строим интерполяционный полином x=L_n( y )

в) Подставляем в этот полином значение y * и получаем x * :

Как правило, решения задачи, полученные первым и вторым способом, будут различными.

Численное дифференцирование – это вычисление производных от функций, заданных в виде таблицы. Задача решается в два этапа. На первом этапе строится интерполяционный полином. На втором этапе находятся производные (первая, вторая и т.д.) от этого полинома.

Если шаг постоянный, то на первом этапе строят ИПН.

Найдем первую производную от этого полинома.

Если производную нужно вычислить в каком-либо узле таблицы (например, в точке х=х₀), то формулы (3.9) и (3.10) упрощаются, так как q₁=0.

Задача численного дифференцирования относится к числу некорректных задач. Это означает, что сколь угодно малые погрешности в исходных данных могут привести к большим погрешностям результата решения, поэтому к численному дифференцированию не следует прибегать без особой необходимости. По тем же причинам обычно не вычисляют производные старших порядков.

Пример. Функция задана в виде таблицы из четырех точек. Вычислить значение функции в точке х=-1 и значение первой и второй производной в этой же точке.

Численное интегрирование – это вычисление определенных интегралов от функций, заданных либо в явном виде (например, Undetermined error: ), либо в виде таблицы. В любом случае функцию приводят к табличному виду, задавая шаг h и вычисляя значения подынтегральной функции в определенных точках. Интегралы вычисляют с помощью так называемых квадратурных формул, то есть

К численному интегрированию прибегают тогда, когда интеграл либо невозможно вычислить точными методами, либо это сделать сложно.

Для нахождения коэффициентов A_i в формуле (3.13) функцию y=f(x) заменяют интерполяционным полиномом. Интеграл от полинома легко вычисляется.

Для нахождения двойных определенных интегралов существуют соответствующие кубатурные формулы (с двойными суммами).

Существует множество квадратурных формул. Рассмотрим три из них.

1. Формулы прямоугольников

а) формула левых прямоугольников

На отрезке [ a , b ] функцию заменяют прямой и считают, что интеграл (то есть площадь криволинейной трапеции, ограниченной осью Х, прямыми х=а , х=в и графиком функции y=f(x)) приближенно равен площади прямоугольника:

в) формула правых прямоугольников

На отрезке [ a , b ] функцию y=f(x) заменяют прямой y=f(b) и считают, что интеграл приближенно равен площади прямоугольника:

с) формула центральных прямоугольников

На отрезке [ a , b ] функцию y=f(x) заменяют прямой y=f((a+b)/2) и считают, что интеграл приближенно равен площади прямоугольника:

(3.16)

2. Формула трапеций

На отрезке [ a , b ] функцию y=f(x) заменяют полиномом первой степени, проходящим через точки ( a , f(a)) и ( b , f ( b )) и считают, что интеграл приближенно равен площади прямоугольной трапеции:

3. Формула Симпсона

На отрезке [a , b] функцию заменяют полиномом второй степени, проходящим через точки (a , f(a)) , (((a+b)/2,f((a+b)/2)))и ( b , f ( b )) и считают, что интеграл приближенно равен площади заштрихованной криволинейной трапеции:

Из рисунков видно, что чем больше длина отрезка [a , b], тем, как правило, больше погрешность, то есть разность между точным значением интеграла и приближенным, полученным по соответствующей квадратурной формуле. Для уменьшения этой погрешности поступают следующим образом. Отрезок [a , b] разбивается на n частей. Для простоты будем считать, что эти части равные, то есть h_i=x_i+1-x_i=h=const. На каждом из отрезков [x_i , x_i ₊₁] используется соответствующая формула. Получают так называемые обобщенные формулы.

1а. Обобщенная формула левых прямоугольников

1 b . Обобщенная формула правых прямоугольников

1с. Обобщенная формула центральных прямоугольников

2а. Обобщенная формула трапеций

3а. Обобщенная формула Симпсона

Число точек в формуле Симпсона должно быть нечетным.

Чем больше n , тем, как правило, меньше погрешность. Формулы дают следующую погрешность. Погрешность обобщенных формул левых и правых прямоугольников – o( h ), погрешность обобщенной формулы центральных прямоугольников и обобщенной формулы трапеций – o( h 2 ). погрешность обобщенной формулы Симпсона – o( h 4 ) .

Каждую из формул нетрудно запрограммировать.

Взять шаг равным одной четвертой длины интервала интегрирования.

Табличный процессор Excel позволяет не только быстро производить различные вычисления, но и решать достаточно сложные задачи. Например, с его помощью можно осуществлять математическое моделирование на основе набора дискретных значений той или иной функции, в том числе находить промежуточное значение функций методом интерполяции. В Excel для этого предусмотрены различные инструменты, пользоваться которыми научит эта статья.

Метод интерполяции: что это такое?

В вычислительной математике так называют способ нахождения промежуточных неизвестных значений функции Y(X) по дискретному набору уже известных.

Интерполяция функции Y(X) может осуществляться только для тех ее аргументов, которые находятся внутри интервала [X₀, X_n], такого, что известны значения Y(X₀) и Y(X_n).

Если X не принадлежит [X₀, X_n], то можно использовать метод экстраполяции.

В классической постановке интерполяционной задачи требуется найти приближенную аналитическую функцию f(X), у которой значения в узловых точках X_i совпадают со значениями Y(X_i) исходной таблицы, т. е. соблюдается условие f (X_i)=Y_i (i = 0,1,2. n).

Линейная интерполяция в Excel

Рассмотрим данные, размещенные в в таблице, представленной ниже.

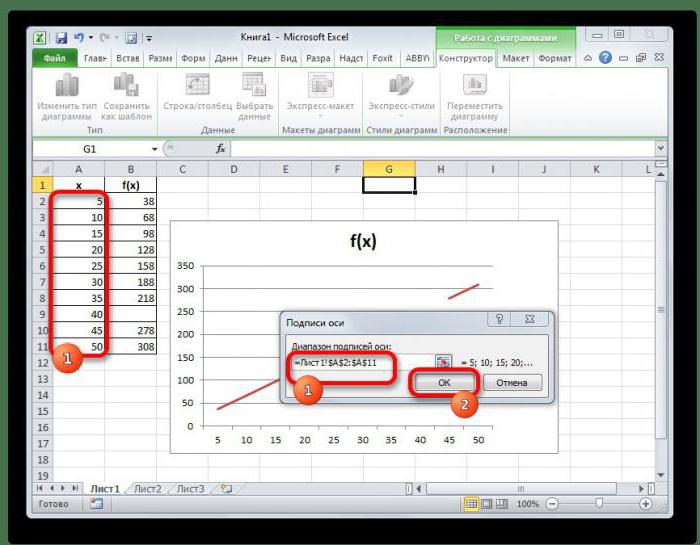
В первом столбце находятся аргументы x, а во втором — соответствующие им значения некоторой линейной функции f(x). Предположим, что нам нужно узнать значение для аргумента x=28. Для этого:

В результате в выделенной ячейке C1 отображается значение 176, являющееся итогом процедуры интерполяции.

Графический метод: подготовка

Интерполяция в Excel, пример которой представлен выше, далеко не единственный способ, позволяющий выяснить промежуточные неизвестные значения функции Y(X) по дискретному набору уже известных. В частности, может быть применен графический метод. Он может оказаться полезным, если в таблице к одному из аргументов не указано соответствующее значение функции, как в той, что представлена ниже (см. ячейку с адресом B9).

Интерполяция в Excel в таком случае начинается с построения графика. Для этого:

Так как в ячейке B9 пусто, график получился разорванный. Кроме того, на нем присутствует дополнительная линия X, в которой нет необходимости, а на горизонтальной оси вместо значений аргумента указаны пункты по порядку.

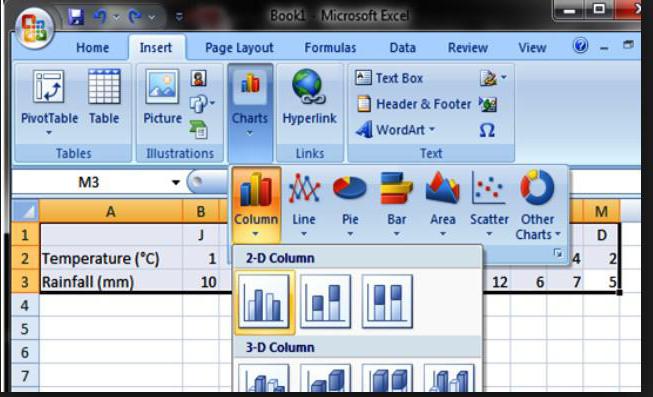
Интерполяция в Excel: решение графическим методом

Займемся обработкой графика. Для этого выделяют сплошную синюю линию и удаляют ее нажатием кнопки Delete, которая находится на клавиатуре.

Если все сделано правильно, разрыв будет удален, а путем наведения курсора на нужную точку графика можно будет увидеть соответствующие значения аргумента и функции.

Использование специальной функции НД

Предположим, что график уже построен, на нем уже установлены корректные подписи шкалы. Попробуем ликвидировать разрыв. Для этого:

Билинейная интерполяция

Круг задач, для решения которых можно использовать моделирование посредством функций одной переменной, достаточно ограничен. Поэтому имеет смысл рассмотреть, как используется формула двойной интерполяции в Excel. Примеры могут быть самыми разными. Например: имеется таблица (см. ниже).

Требуется вычислить давление ветра при величине пролета 300 м на высоте 25 м.

В таблицу добавляют новые записи так, как представлено на рисунке (см. ниже).

Как видно, в нее добавлены ячейки для высоты и пролета в J1 и J2.

Использование spline

Предыдущий метод достаточно громоздкий, поэтому в некоторых случаях предпочтительнее интерполяция сплайнами. В Excel ее суть заключается в нахождении интерполирующей функции f(Х) по формулам одного и того же типа для различных подмножеств аргумента. Далее осуществляется стыковка значений f(Х) и ее производных на граничных значениях аргументов каждого из подмножеств. В Excel для этих целей предусмотрены специальные функции, а также возможно написание макросов на VBA. Однако они должны создаваться под конкретную задачу, поэтому их изучение в общем виде не имеет смысла.

Теперь вы знаете, как написать формулу двойной интерполяции в Excel корректно или найти неизвестное значение линейной функции посредством встроенных операторов или графика. Надеемся, что эта информация поможет вам в решении множества практических задач.

Читайте также: