Как сделать синусоида из бумаги
Если вам нужно нарисовать синусоиду в PowerPoint для презентаций, то здесь мы покажем различные подходы, которые можно использовать в зависимости от ваших потребностей.
Синусоида или синусоидальная волна представляет собой математическую кривую, которая описывает плавный повторяющиеся колебания. Она названа в честь функции синус, из которого она является граф. В соответствии с Википедии, синусоида часто происходит в чистой и прикладной математики, а также физики, техники, обработки сигналов и многих других областях, в том числе звукорежиссуры, строительной техники, музыкальных приложений, аэрокосмической промышленности, электротехники и многое другое. Например, колебание незатухающой системы весенне-масс вокруг равновесия является синусоида может быть смоделирована с синусоидальной способом, или вы можете также смоделировать колебание маятника.
1. Используйте Fooplot нарисовать идеальную кривую синусоида для PowerPoint
Как мы уже видели, Fooplot хороший онлайн инструмент, который позволяет создавать графики и сюжет какой-либо функции в Интернете. Мы можем указать грех и соз и сделать хорошую синусоиду для наших презентаций PowerPoint, а также другие математические графики для презентаций. Вы можете также использовать эту функцию, чтобы сделать шаблоны математические функции PowerPoint для загрузки.
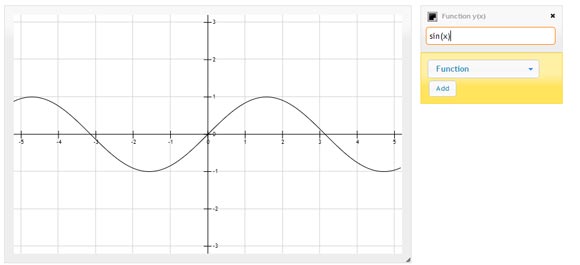
После этого вы можете сгенерировать выходной файл как PNG или любой другой формат, и вставить его в PowerPoint 2010. Ниже вы можете увидеть пример PowerPoint слайд, показывающий функцию sin (х).
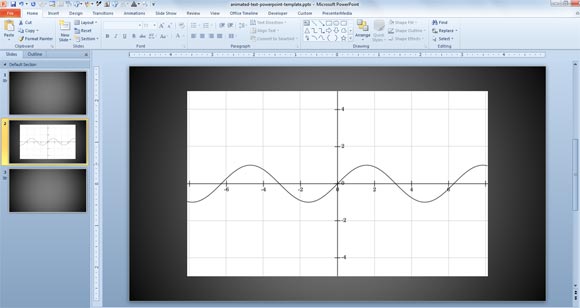
2. Участок синусоидальной волны с помощью кривых Безье
Другой подход сделать этот вид кривых с помощью кривых Безье. Тем не менее, результат вы можете получить с помощью этих кривых не может быть совершенным. В зависимости от ваших потребностей презентации, вы можете выбрать между созданием синусоиде, используя этот подход или более точный подход, как построение синусоиду в Fooplot или Matlab.


Рисунок синусоидальной волны с помощью кривых Безье может быть не очень практичным на первый взгляд, и вам нужно отредактировать точки, чтобы сделать его более точным. Вы можете проследить в PowerPoint с помощью метода трассировки, что мы ниже объяснена над грехом (х) сюжет, созданный ранее как изображение. Тогда вы можете представить простую синусоиду волны, как в приведенном выше примере.
3. Нарисуйте синусоиды в Excel и вставить его в PowerPoint
Другой подход должен был бы сделать синусоидальную кривую в Excel с помощью функции Excel греховную, а затем скопировать и вставить полученный рисунок в PowerPoint слайд. Используя этот подход. Для построения синусоиды в Excel можно использовать инструкции в этом формате PDF. В основном то, что она предлагает, чтобы создать таблицу со следующей информацией: (. Сек) Ввод частоты, Omega, амплитуда и Delta T.
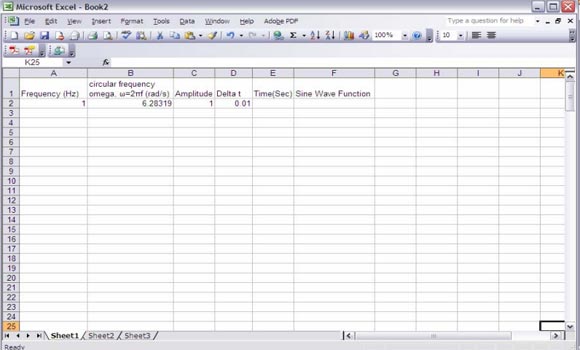
Затем введите начальное время (в данном примере равен нулю) и заполнить колонку времени, используя уравнение авш Т + 1 = T + дельта. Теперь вы можете заполнить значения в рамках функции синусоида с помощью функции sin () в Excel.
Наконец, используйте XY график рассеяния для создания диаграммы.
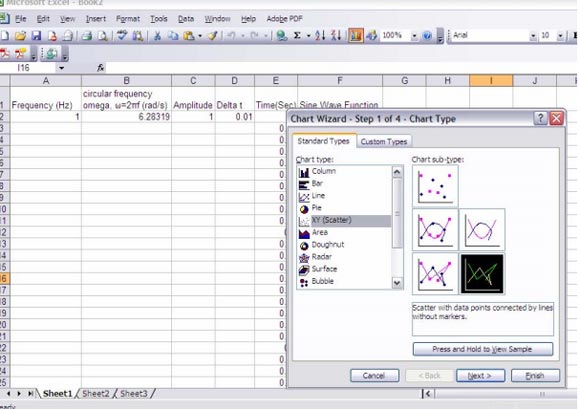
Когда вы будете готовы, вы можете скопировать и вставить сюжет в презентации PowerPoint.
У многих учеников возникают проблемы с этой темой, в основном, из-за непонимания общего смысла тригонометрии. В этой статье я постараюсь помочь вам разобраться зачем нужна тригонометрия и расскажу про лайфхак, чтобы не учить значения синуса и косинуса.
К моменту начала изучения тригонометрии Вы, скорее всего, уже знаете: определение прямоугольного треугольника и окружности — этого вполне достаточно для понимания темы.
*прошу заметить, что некоторые формулировки могут не соответствовать действительности - это сделано для того, чтобы вы лучше запомнили основы. Точные понятия и определения расскажет ваш учитель математики.
Что такое синус и косинус?
Изначально не было никакой окружности. Изучая треугольники, древние ученые выражали углы через соотношение сторон. То-есть синусы и косинусы появились раньше градусной меры углов.
Поскольку угол может быть найден через разные соотношения сторон, решили дать им названия: синус и косинус.
Синус - это отношение стороны треугольника, лежащей напротив данного угла, к гипотенузе (большей стороне).
Косинус - это отношение прилежащей стороны к гипотенузе.
Думаю не ошибусь, если скажу, что теорема Пифагора - самая полезная теорема в геометрии. Давайте применим её для данного треугольника:

В этом видеоуроке мы познакомимся с линией, которую называют эллипсом. Рассмотрим частный случай эллипса. Также познакомимся с такими линиями, как гипербола и парабола. Поговорим о конусе. Узнаем, какую кривую называют спиралью Архимеда. Выясним, какие кривые называют синусоидой, кардиоидой, циклоидой. Узнаем, какие линии называют гипоциклоидами.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Замечательные кривые"
Давайте с вами возьмём плотный лист бумаги, прикрепим к нему в двух точках нитку и натянем карандашом эту нитку. Теперь, двигая карандаш и натягивая нитку, нарисуем линию.

Линия, которая у нас получилась, называется эллипсом. Заданные две точки называются фокусами эллипса.

Обратите внимание, что все точки эллипса обладают следующим свойством: сумма расстояний от любой точки эллипса до его фокусов постоянна.
Эллипсы в нашей жизни встречаются гораздо чаще, чем кажется. Так, например, когда мы режем наискосок колбасу, то получающееся сечение имеет эллиптическую форму. Планеты движутся вокруг Солнца по эллиптическим орбитам, причём Солнце находится в одном из фокусов. В архитектуре встречаются элементы, которые напоминают нам эллипс.
Окружность – частный случай эллипса, она получается, если фокусы эллипса совпадают.
На одном из предыдущих занятий мы говорили об окружности и её элементах. Мы научились её строить с помощью циркуля.

Познакомимся со следующей замечательной кривой – гиперболой.

Для этой кривой мы не можем предложить, как в предыдущем случае, достаточно простой способ, позволяющий вычертить гиперболу и одновременно показывающий её основное свойство. Поэтому сразу сформулируем основное свойство, задающее гиперболу.
Гипербола – это линия, для всех точек которой разность расстояний до двух заданных точек плоскости (фокусов гиперболы) есть величина постоянная.


То есть можем записать следующее равенство: .
Вы обратили внимание, что гипербола состоит из двух частей (двух отдельных ветвей). Все точки одной ветви ближе к одному фокусу (соответствующим образом берётся и разность расстояний), а другой ветви к другому фокусу.

Теперь познакомимся с параболой. Возьмём на плоскости прямую l и точку F. Затем отметим на плоскости точку М, которая равноудалена от точки F и от прямой l. Расстояние от точки до прямой – это длина перпендикуляра, проведённого из этой точки к данной прямой. Тогда можем записать, что .
Такие точки (равноудалённые от точки F и от прямой l) описывают замечательную кривую, которая называется параболой.

Эта замечательная кривая не так уж редка в природе. Камень, брошенный человеком под углом к поверхности Земли, описывает параболу.
Ну а теперь поговорим о конусе. Наверное, каждый из вас представляет, что такое конус. Крыши башен часто имеют форму конуса. Архитекторы часто используют такие формы для создания эффекта устремлённости здания вверх.
Конус состоит из двух частей (пол), имеющих общую вершину. Из листа бумаги можно свернуть одну часть.

Математики определяют конус следующим образом. Итак, возьмём окружность и точку над её центром. Эта точка – вершина конуса. Проводя прямые, соединяющие всевозможные точки окружности с вершиной, получим коническую поверхность.

Конус можно пересечь плоскостью по окружности. А вот если плоскость сечения наклонять, то получим эллипс. И чем больше мы будем наклонять плоскость сечения, тем всё более вытянутые эллипсы будут получаться.



Итак, можем сделать вывод, что все рассмотренные выше линии (эллипс, гипербола и парабола) объединяются общим свойством. Каждая из них может быть получена при пересечении конуса плоскостью. Поэтому их называют коническими сечениями.
Сейчас давайте посмотрим на равномерно вращающийся диск, по радиусу которого ползёт муравей. Проползая вперёд, он одновременно смещается в сторону вращения диска.


В природе спираль Архимеда встречается на каждом шагу.
Теперь сделаем из плотной бумаги, свернув её несколько раз, трубочку. Разрежем эту трубочку наклонно. Если трубочку не разворачивать, то в сечении будет эллипс.

А вот если трубочку развернуть, то посмотрите, какую линию образует разрез.

Перерисуем эту линию… Это одна из замечательных кривых, которую называют синусоидой.

Далее вырежем из картона два одинаковых круга. Один из них закрепим неподвижно. Второй круг приложим к первому и отметим на его краю точку, которая наиболее удалена от центра первого круга. Теперь прокатим без скольжения подвижный круг по неподвижному. Обратите внимание, какую линию описала точка.

Начертим эту линию.

Теперь представим, что по прямой линии без скольжения катится круг, на границе окружности которого взята точка. Посмотрите на траекторию, которую опишет при этом точка. Получившаяся кривая называется циклоидой.

Циклоида обладает многими замечательными свойствами. Вот, например, одно из них. Давно математики пытались решить вот такую задачу: какой формы должен быть гладкий жёлоб, соединяющий две точки – А и B (А выше, чем B), чтобы гладкий металлический шарик скатился по этому жёлобу из точки А в точку B под действием своего веса за кратчайшее время?
Можно подумать, что жёлоб должен быть прямолинейным. Но это не так.
Может быть, жёлоб нужно выгнуть по дуге окружности? Так же думал и великий итальянский физик, астроном и математик Галилео Галилей, живший на рубеже 16-17 веков, но он ошибался.
Иоганн Бернулли – швейцарский математик, механик, врач и филолог-классицист – в одна тысяча шестьсот девяноста шестом году установил, что жёлоб должен быть выгнут по циклоиде, опрокинутой вниз.
Получается, что, скатываясь на санях по снежной горке, форма которой близка к опрокинутой циклоиде, мы окажемся у основания этой горки быстрее, чем в случае другой формы горки.

Сейчас возьмём кусок толстого картона и вырежем в нём круг радиусом 12 см. Из такого же картона вырежем три круга радиусами 4 см, 3 см и 2 см.
Далее вложим в круглое отверстие в картоне круг радиусом 4 см, чтобы он касался края. При этом на окружности этого круга отметим точку А.

Проследим за тем, какую линию опишет отмеченная точка А, когда кружок покатится по окружности выреза без скольжения. Посмотрите, какая линия получилась…

Проделаем то же самое с кругом с радиусом 3 см. Посмотрите, какую линию при этом описала точка А…

И проделаем то же самое ещё раз, но с кругом с радиусом 2 сантиметра. Посмотрите, какую линию описала точка А сейчас…

Популярная уточка Лалафанфан
Вы можете приобрести куклу Лалафанфан с уже готовым набором базовых вещей, но это может стоить значительной суммы (от 2000 рублей). Но можно сделать всё проще, и создать уточку Лалафанфан из бумаги, раскрасив её с помощью фломастеров. Также с помощью бумаги и фломастеров вы сможете создать подходящую одежду для вашей уточки, и одеть её в те фасоны, которые ей подойдут в соответствии с вашим вкусом.
Давайте подробно разберём инструкцию, по которой вы сможете сделать уточку Lalafanfan и одежду для неё из листов обычной бумаги.

Как вырезать уточку Лалалфанфан из бумаги – подробное руководство
Для создания понравившейся уточки понадобится несколько листов бумаги формата А4, набор различных фломастеров (маркеров), карандаш, ножницы и прозрачный односторонний скотч. Для крепления одежды на уточку также будет нужен двухсторонний скотч.
Собрав все нужные инструменты, переходим к созданию уточки. Выполните следующее.
Часть 1. Создание контуров уточки
Возьмите обычный лист бумаги А4, поставьте его горизонтально, и сложите его пополам. Проведите вертикальную линию 15 сантиметров длиной в центре листа. Поставьте на концах линии отрезки.

Сверху вниз от линии отступите 7 сантиметров. Эти 7 сантиметров будут предназначаться для создания головы нашего персонажа. Остальные 8 сантиметров будут являться его телом. На средней отметке также проведите горизонтальную линию.

Теперь в части головы от центральной линии отступите 5 сантиметров влево и вправо и поставьте вертикальные чёрточки.

Далее отступите 3 сантиметра от линии будущего куклы тела с двух сторон, и там также поставьте вертикальные чёрточки.

Теперь сверху в очерченных границах нарисуйте большую голову. На самом верху головы в центре нарисуйте маленький прямоугольничек (чубчик уточки).

В нижней части по линиям закруглите ножки (можно сделать между ними небольшое пространство).

От головы к ногам проведите небольшие закруглённые ручки.

Дальше на голове проведите горизонтальную линию. Под ней по центру поставьте наметки, где у нас будут глаза уточки.

С двух сторон головы нарисуйте большие круглые щеки.

Под глазками, между щеками сделайте набросок клювика.
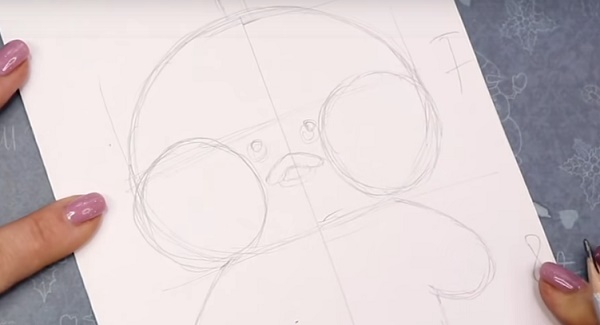
Часть 2. Раскраска уточки Лалафанфан
Разбирая хитрости рисования уточки на бумаге из Тик Тока переходим к этапу её раскраски. Весь имеющийся у нас набросок можно стереть ластиком так, чтобы остались еле видны границы намеченного. Это будет каркас нашего рисунка, который нам предстоит раскрасить.



Теперь чёрным фломастером наведите чёрные горошины – глаза уточки. Также тонким чёрным фломастером нарисуйте клювик в виде изогнутой колбаски.
Снизу дорисуйте две изогнутые линии, которые станут нижней частью клювика.

Далее обведите тонким фломастером остальной контур уточки, включая кружочки-щёчки.

Раскрасьте ярко оранжевым цветом клювик.

Для раскраски внутренней части клювика можно выбрать цвет потемнее.

Часть 3. Придание уточки долговечности с помощью скотча
Не забываем о придании нашему рисунку долговечности. После раскраски уточки берём ножницы и широкий прозрачный скотч. Нам нужно покрыть полосками скотча всю уточку, чтобы она была износостойкой, и мы бы могли удобно менять на ней одежду.
После того, как мы заклеили скотчем бумагу, необходимо вырезать уточку с обеими частями листика.

После вырезания обратную сторону уточки также можно закрасить жёлтым и при желании заламинировать. Наша уточка готова.
Часть 4. Подготовка одежды для уточки
После создания уточки из Тик Тока на бумаге необходимо сделать для уточки одежду одежду – например шапочку и шубку. Ставим нашу уточку на лист бумаги, обводим её контур.
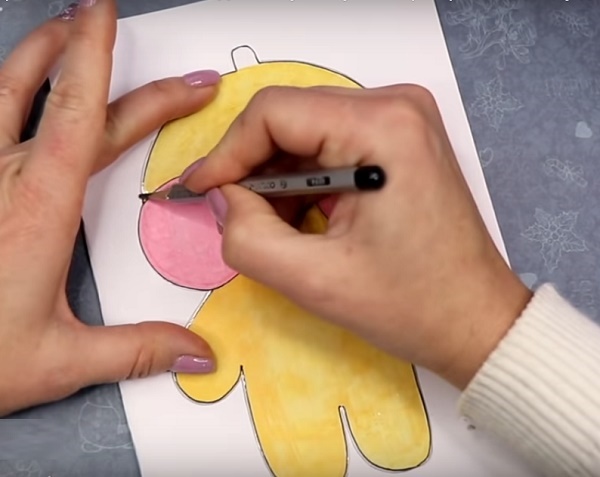
Помечаем, на обведённой бумаге, где у уточки глаза и край верхних щёк, чтобы понимать, где нам рисовать шапочку.

Далее проведите для шапочки изогнутую линию, нарисуйте полосочку для шапки, а затем сверху дорисуйте для линии круглую шапочку с бубоном. Бубон рисуем так, чтобы бубон закрывал уголочек уточки.

Теперь шубка. Делаем широкую кайму для уточки, прорисовываем меховые рукавчики для ручек и ножек уточки.

Теперь обводим все элементы ручкой.

Затем раскрашиваем шубку. Сначала используется маркер цвета.185 (тёмно-голубой – будет основной цвет), и на шапке. На мех (манжеты) маркер 143 – небесно голубой.
Далее серебристым цветом можно нарисовать на шапке снежинки, на воротнике, и еще мелкие точки можно поставить на платьице. Платьице с шапкой готово.

Всё опять покрываем скотчем. На шапку понадобится две полоски прозрачного скотча. Отдельно 3 полоски на платье.
Вырежьте шапку отдельно и платье отдельно аккуратно. Наша новогодняя одежда готова.

Накладываем её на уточку. Приклеивать одёжку можно также на двухсторонний скотч. Один кусочек крепим на шапку, и второй на платье. Затем отрываем эти полосочки, и полученной липкой основой прикрепляем одежду к уточке.

Видео
В нашем материале мы разобрали создание уточки Лалафанфан, так популярную в Тик Ток, на Ютуб и Инстаграм. Возможно, ваша первая уточка не получится такой симметричной, как на наших изображениях. Но попрактиковавшись должным образом и набив руку, вы сможете создать красивую уточку и различные наряды к ней, и использовать её при создании ваших роликов в популярной сети Тик Ток.

Читайте также:
