Бутылка клейна оригами
Математики так легко переходят из одного n-мерного пространства в другое, что порой создаётся впечатление, что пространства размерности 5, 7, 24 и т.д. это обыденная вещь. Например, фраза "Рассмотрим четырехмерную сферу. " не вызывает ни у кого шока и недоумения. Хотя как можно рас смотр еть что-то подобное? Люди, живущие в пещерах, пытаются представить солнце.
Но в этом и состоит великая мощь человеческого разума. Мы можем рассматривать и изучать вещи за гранью нашей реальности, просто опираясь на логические выводы и имеющийся опыт. Что такое сфера? Это множество точек равноудалённых от заданной ( центра сферы ). В одномерном мире, то есть на прямой, сфера представляет собой отрезок, в двухмерном - окружность, в трехмерном, то что каждый представляет себе как сферу.
Мы не в силах представить, как она будет выглядеть в четырехмерном пространстве. Но определение будет всё тоже и этого достаточно. А если кому-то не хватает конкретики, то есть довольно симпатичный образ. Рассмотрим, что будет если двухмерная сфера (окружность) будет пересекать одномерный мир. Какой след она оставит? Этот процесс легко смоделировать на бумаге.
Мы видим, что на прямой последовательно появляются отрезки, которые сначала увеличиваются, а затем уменьшаются. То же самое будет происходить, если трёхмерная сфера будет пересекать двухмерный мир (плоскость). На плоскости будут образовываться окружности, диаметр которых сначала будет увеличиваться, а затем уменьшаться.
Если однажды, вы заметите трехмерную сферу растущую, а потом уменьшающуюся в диаметре, можете быть уверены, что существа из четырехмерного пространства заглянули к нам на своём сферическом корабле.
Легкость перехода из пространства меньшего порядка в пространство большего может создать иллюзию, что обратный переход так же возможен и прост. Нужно внимательно следить за тем, что вы приносите с другой стороны. Далеко не все свойства объекта сохраняться, при таком переходе. А в некоторых случаях, сами объекты не смогут существовать в нашем пространстве.
Подобная неаккуратность произошла с бутылкой Клейна. Топологическим объектом, который существует в четырехмерном пространстве. Но вы можете найти умельцев, которые создают и продают нечто, что они называют бутылкой Клейна. Не попадайтесь на это. То, что вы получите, будет лишь приблизительным образом, моделью. Им стоило бы делать приписки "типа", "как бы" или "бутылкаклейносодержащий продукт".
Что же с ней не так?
Подобно листу Мёбиуса , бутылка Клейна является неориентируемой поверхностью, то есть у неё также нет другой стороны. (я вынуждена настаивать, что у листа Мёбиуса только одна сторона ). По существу, вопрос сводиться к тому, сможем ли мы, двигаясь по замкнутому пути на поверхности, в какой-то момент оказаться в том же месте, но с другой стороны?
Как бы вы не двигались по сфере, вы никогда не сможете попасть внутрь, пока не начнете копать. Такая же ситуация с тором. (Не богом, а бубликом, хотя в топологическом смысле человек и есть тор. Тут можно было бы поднять философско-религиозный вопрос, но это сильно уведёт от темы.) Когда мы движемся по листу Мёбиуса мы попадаем в ту же точку, с "другой" стороны, пройдя по замкнутому контуру. То же самое должно происходить с бутылкой Клейна. Когда вы находитесь на ней, вы одновременно и внутри и снаружи. Это условие не выполняется для тех изделий, которые продаются под видом бутылки. Особенно забавно это выглядит, когда в них что-то налито.
Еще неделю назад я практически ничего не знал про 3d принтеры.
Но они обладают какой-то мистической притягивающей аурой, и вот все мысли теперь только о них. (Учитывая, что дети вовсю резвятся с этими штуками, и на что способны эти девайсы.)
После недолгого гугления я нашел, где в Москве можно комфортно экспериментировать с этими штуками из будущего.
Чтобы стать мастером кунг-фу трехмерной печати, я ставлю для себя следующие этапы:

Итак, я приступил к реализации пункта 1.
Вот что получилось в итоге
Статистика:
Длина нити 162 метра
Время печати: 1 час 22 минуты 38 секунд
Масса пластика 11.5 г
Объем пластика 10.7 см в кубе
Ниже описал процесс по шагам

Далее сохраняем G-code (набор управляющих команд для принтера) на SD-карту, и вставляем эту карточку в нашего красавца:

Далее принтер разогревается и начинает печатать:










Сначала появилось это.
А уже после с помощью этого Клейну пришло в голову так называемая бутылка Клейна.

краствая бутылка
прочитал весь текст, так и не нашел самого главного и интересного факта - у этой бутылки нет дна.
а в целом согласен с чуваком выше, эта тема хотя бы интересна, в отличии от погоды в вашем городе
кстати, в Тюмени -20C :D
Откуда столько плюсов. Автор же вообще никакой информации не донес!
-Сказал только в каком году придумали ее (кого ее, что за бутылки, ее смысл и тд)
-Сказал что ее сложно сделать
-Сказал, что она была в футураме.
А при чём тут наука? Хотя бы написал зачем она нужна, кто её придумал и т.д. А так ниочём. Если будешь выкладывать в следующий раз подумай больше о "научной стороне".
Чувствую, в Бельгии скоро на самом деле пиво в такой таре начнут продавать. Они мастера на всякие интересные емкости.
Спасибо за интеллектуальный пост! Вот на этом-то еще и держится старый пикабу))) Выкладывай еще пожалуйста.
Ну а главного, того, что бутылка Клейна - это четфрёхмерный аналог ленты мёбиуса, и нету =(
В четырёхмерном пространстве поверхность бутылки не пересекает сама себя, но тем не менее образует замкнутое множество, которое тоже как бы "имеет только одну сторону", как и лента Мёбиуса в трёхмерном пространстве.
в чём прикол обсуждать бутылку, которая не реальна в нашем 3х мерном мире. даже если бы она была реальна, видно что практической пользы от неё нет !

Так значит дно является одновременно и горлышком?
Чуйка
Первое свидание
Подслушано вчера. Уютное кафе. Я сижу за столиком, жду подругу. Рядом столик за котором примостились мальчик с девочкой, на вид не больше 14 - 15 лет.
Он - в какой школе учишься?
Она - не отрываясь от смартфона, в пятой.
Он - а чем занимаешься, что любишь, куда ходишь?
Она - не отрываясь от смартфона, да так, "всяко разно"
Он - ты в тик -токе ответы подглядываешь?
Она фыркнула и упорхнула из-за столика в закат. И вот честно, так гордо стало за этого парня.
А он сидел за столиком, пил кофе и чему - то улыбался)))
Зачем?

Мне крышка

Спасибо.


Назовите город, который изменил вашу жизнь
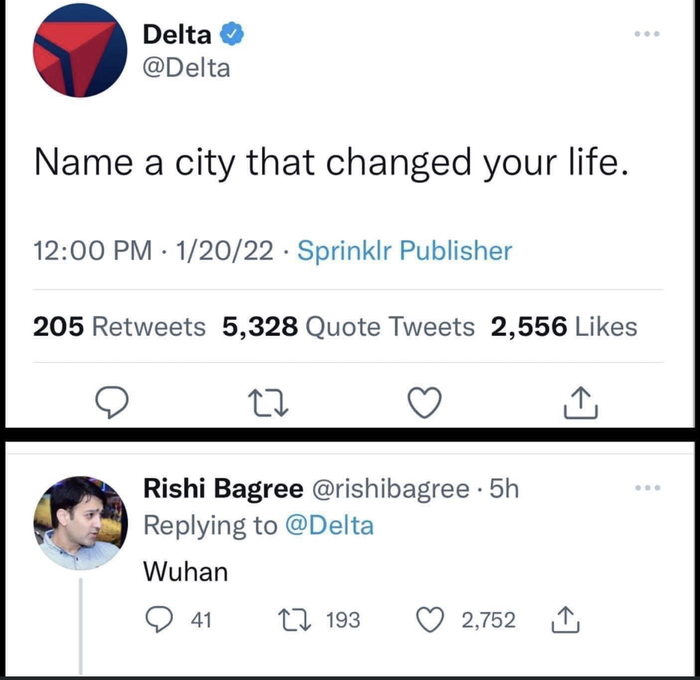
Гениально))) Как я его понимаю)))
Иногда так хочется так же сделать.

Медики Башкирии готовят забастовку

Забастовки и медицина — понятия несовместимые. Мы – врачи, медики всегда на фронте и передовой, мы жизнь спасаем, а бастовать — это как дезертировать. В медицину никогда не шли за деньгами, шли по убеждениям. Врач может работать в любой профессии, но врачом может быть только врач…
Мы выражаем поддержку справедливым требованиям медиков и будем следить за развитием событий.





ВСЕ ЗАГАДКИ И ПРИМЕНЕНИЕ БУТЫЛКИ КЛЕЙНА

Автор работы награжден дипломом победителя III степени
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF
Феликс Христиан Клейн
1.2 Основные достижения
Загадки бутылки Клейна
2.1 Строение бутылки Клейна
2.2 Конструирование бутылки Клейна
ВВЕДЕНИЕ
Тема работы и обоснование выбора темы
Предлагаемая вниманию читателя исследовательская работа посвящена необычной и загадочной бутылке Клейна.
Я обратила на нее внимание после того, как наткнулась на очень интересную статью в Интернете по поводу самых причудливо-простых изобретений. Свою будущую жизнь я хотела бы связать с математикой и физикой, поэтому данный прибор меня заинтересовал своим строением.
Актуальность темы моей работы определяется тем, что современные учащиеся считают математику и физику одними из самых скучных и бесполезных предметов, хотя на самом деле все, что нас окружает, в той или иной степени взаимосвязано с математикой и физикой, а это, кстати говоря, очень интересно.
На сегодняшний день существует множество работ по данной теме. Но новизна моей работы состоит в том, что таким образом я хочу показать учащимся математику и физику с занимательной интересной стороны, а не доказать какие-либо факты или закономерности.
Основной целью моей работы является рассмотрение бутылки Клейна с точки зрения математики.
Для достижения поставленной цели нам необходимо решить следующие задачи:
Охарактеризовать биографию Феликса Клейна;
Познакомится с основными достижениями Клейна;
Рассмотреть особенности строения бутылки Клейна;
Выявить способы конструирования бутылки Клейна.
Глава 1
Научная деятельность Феликса Клейна.
Биография Феликса Клейна
Феликс Христиан Клейн родился 25 апреля 1849 в Дюссельдорфе, в семье чиновника. Окончил гимназию в Дюссельдорфе, затем учился математике и физике в Боннском университете. Сначала планировал стать физиком. В это время Юлиус Плюккер заведовал отделением математики и экспериментальной физики в Бонне, и Клейн стал его ассистентом. Однако главным интересом Плюккера была геометрия. Под его руководством Клейн стал доктором в 1868.
В 1868 году Плюккер умер. Клейн совершает поездку по Германии, знакомится с Клебшем и другими крупными математиками.
В 1872 году Клейн становится профессором Эрлангенского университета.
В 1875 году женился на Анне Гегель, стал профессором в Высшей технической школе в Мюнхене. Позже работал в Лейпцигском университете. В1882 году после серьезной болезни, начал заниматься педагогической и общественной работой. С1888 года работал в Гёттингенском университете. Его лекции пользовались большим успехом, слушатели приезжали со всего мира. Умер Клейн на 76 году жизни.
Основные достижения Феликса Клейна
Именем Феликса Клейна названы:
Математический центр в Германии
Кратер на обратной стороне Луны
Приз Европейского математического общества и Технологического университета Кайзерслаутерна (присуждается молодым математикам Европы в ходе Европейского математического конгресса (каждые 4 года) за практически полезные работы в области прикладной математики)
Медаль Международной комиссии по математическому образованию.
Имя Клейна носят следующие математические объекты:
модель (интерпретация) Клейна
бутылка (поверхность) Клейна
На последнем изобретении мы бы хотели остановиться более подробно во второй главе.
Глава 2
Загадки бутылки Клейна.
2.1 Строение бутылки Клейна
Бутылка Клейна — это определённая неориентируемая поверхность (то есть двумерное многообразие). Бутылка Клейна впервые была описана в 1882 г.немецким математиком Ф. Клейном. Она тесно связана с лентой Мёбиусаи проективной плоскостью. Название, по-видимому, происходит от неправильного перевода немецкого слова Flache (поверхность), которое в немецком языке близко по написанию к слову Flasche (бутылка).
Чтобы построить модель бутылки Клейна, понадобится бутылка с двумя дополнительными отверстиями: в донышке и в стенке. Горлышко бутылки нужно вытянуть, изогнуть вниз и, продев его через отверстие в стенке, присоединить к отверстию на дне бутылки. Для настоящей бутылки Клейна в четырёхмерном пространстве отверстие в стенке не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве.
2.2 Конструирование бутылки Клейна
Способ № 1.Получение бутылки Клейна из бумаги. Прежде всего, нужно взять бумажный квадрат, перегнуть его пополам и соединить клейкой лентой его стороны. На обращенной к вам половине квадрата сделайте прорезь, перпендикулярную склеенным сторонам. Расстояние между прорезью и верхним краем трубки должно быть равно примерно четверти стороны квадрата. Согнув модель пополам вдоль пунктирной прямой, протащите нижний край трубки сквозь прорезь и склейте друг с другом верхнее и нижнее основания трубки. Правда, там, где поверхность самопересекается, в нашей модели прорезь, но легко представить себе, что края этой прорези соединены так, чтобы поверхность во всех своих точках была непрерывна и не имела края.
Способ № 2. Получение бутылки Клейна из стандартной пластмассовой бутылки. Необходимо взять бутылку с отверстием в донышке, вытянуть горлышко, изогнуть его вниз, и продев его через отверстие в стенке бутылки (для настоящей бутылки Клейна в четырёхмерном пространстве это отверстие не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве), присоединить к отверстию на дне бутылки.
Способ № 3. Получение бутылки Клейна из одного цилиндра. Один из краёв цилиндра изгибается в обратную сторону, проходит сквозь цилиндр и склеивается с другим краем. Чтобы совершить это склеивание, необходимо исказить ширину цилиндра.
Способ № 4. Получение бутылки Клейна из ткани. Целесообразно взять кусок носка или колготок и проделать с ними то же, что и с цилиндром.
Способ № 5. Получение бутылки Клейна склеиванием двух листов Мёбиуса.Бутылка Клейна может быть получена склеиванием двух лент Мёбиуса по краю. Однако в обычном трехмерном евклидовом пространствесделать это, не создав самопересечения, невозможно.
Заключение
Как представить себе, на что похожа поразительная "бутылка" в реальности? Оказывается, невозможно построить абсолютно правильную модель этого объекта в нашем трехмерном мире: здесь будет наблюдаться пересечение поверхности, что напрочь отсутствует в четырехмерном измерении. Вывод: истинная "бутылка Клейна" может существовать только в четырехмерном измерении! Допустим, у нас есть бутылка с очень длинным горлом, в стенке и в донышке бутылки есть небольшие отверстия, соответствующие размеру горлышка. Берем бутылку за горло, изгибаем его, пропускаем вплотную через боковое отверстие, дотягиваемся горлышком до отверстия в дне бутылки и совмещаем их. Вот и получилось! Где - начало, где - конец? - сказать невозможно . У такой бутылки нет края, и ее поверхности нельзя разделить на внешнюю (наружную) и внутреннюю!
Все вышесказанное подводит нас к мысли, что математика таит в себе много нового, неизведанного и интересного.

Читайте также:
